北师大版数学七年级下册6.2 频率的稳定性(1)数学课件(20张ppt)
文档属性
| 名称 | 北师大版数学七年级下册6.2 频率的稳定性(1)数学课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
初中数学七年级(下)
6.2 频率的稳定性(1)
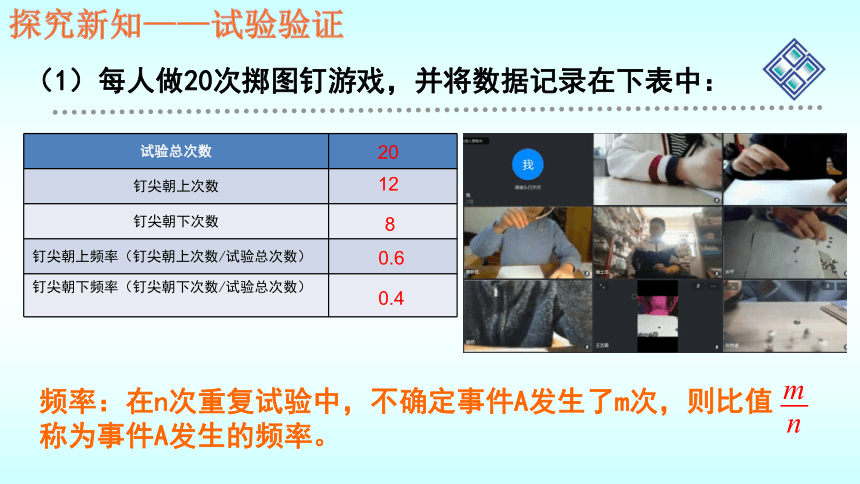
(1)每人做20次掷图钉游戏,并将数据记录在下表中:
20
12
8
0.6
0.4
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
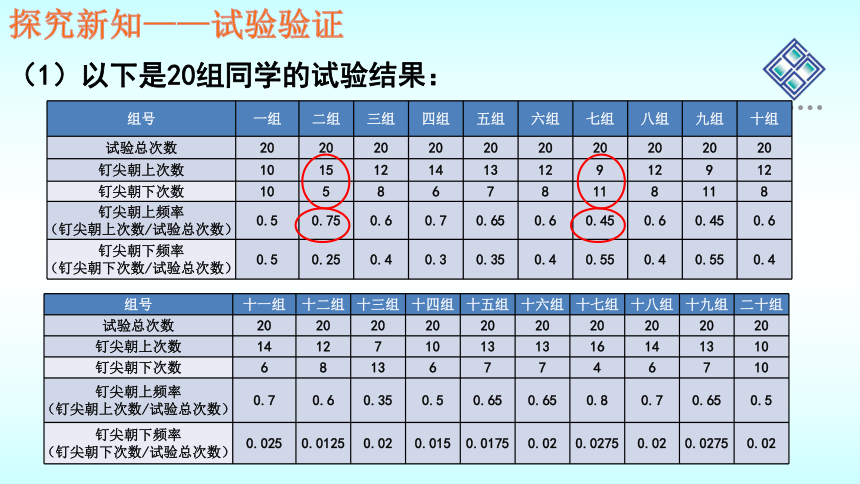
(1)以下是20组同学的试验结果:
组号 一组 二组 三组 四组 五组 六组 七组 八组 九组 十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 10 15 12 14 13 12 9 12 9 12
钉尖朝下次数 10 5 8 6 7 8 11 8 11 8
钉尖朝上频率
(钉尖朝上次数/试验总次数) 0.5 0.75 0.6 0.7 0.65 0.6 0.45 0.6 0.45 0.6
钉尖朝下频率
(钉尖朝下次数/试验总次数) 0.5 0.25 0.4 0.3 0.35 0.4 0.55 0.4 0.55 0.4
组号 十一组 十二组 十三组 十四组 十五组 十六组 十七组 十八组 十九组 二十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 14 12 7 10 13 13 16 14 13 10
钉尖朝下次数 6 8 13 6 7 7 4 6 7 10
钉尖朝上频率
(钉尖朝上次数/试验总次数) 0.7 0.6 0.35 0.5 0.65 0.65 0.8 0.7 0.65 0.5
钉尖朝下频率
(钉尖朝下次数/试验总次数) 0.025 0.0125 0.02 0.015 0.0175 0.02 0.0275 0.02 0.0275 0.02
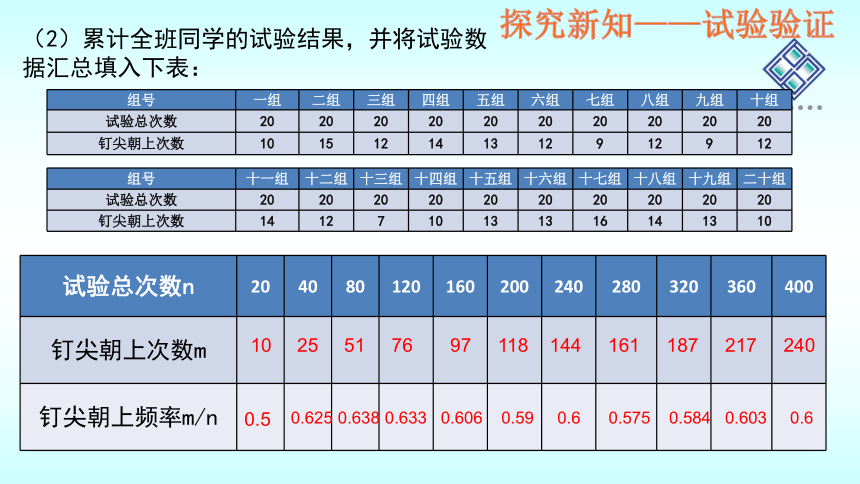
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
10
25
51
0.5
0.625
0.638
76 97 118 144 161 187 217 240
0.633 0.606 0.59 0.6 0.575 0.584 0.603 0.6
试验总次数n 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上次数m
钉尖朝上频率m/n
组号 一组 二组 三组 四组 五组 六组 七组 八组 九组 十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 10 15 12 14 13 12 9 12 9 12
组号 十一组 十二组 十三组 十四组 十五组 十六组 十七组 十八组 十九组 二十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 14 12 7 10 13 13 16 14 13 10
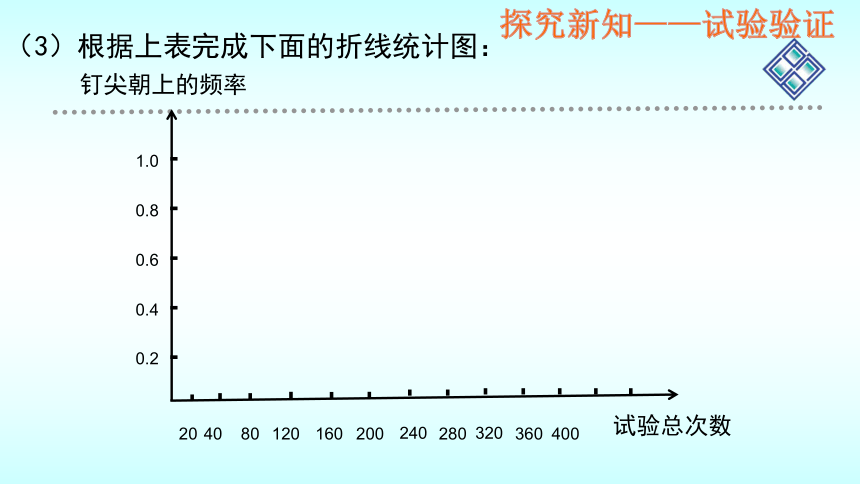
(3)根据上表完成下面的折线统计图:
(3)根据上表完成下面的折线统计图:
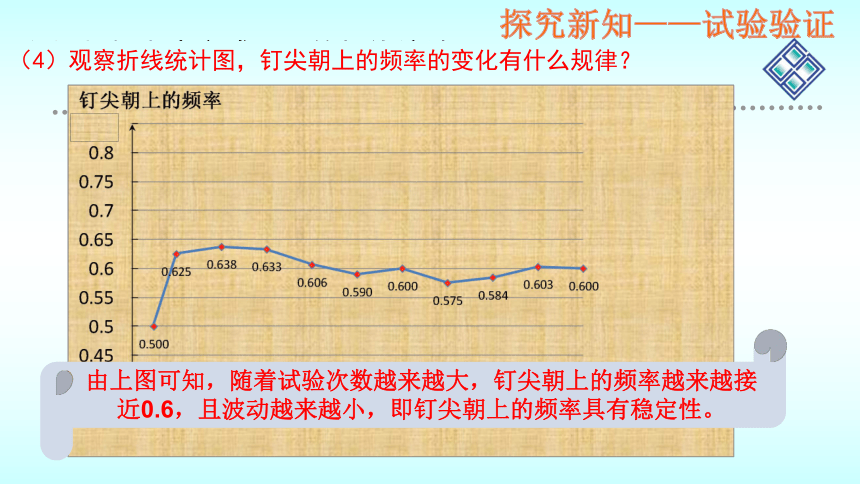
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
20
由上图可知,随着试验次数越来越大,钉尖朝上的频率越来越接近0.6,且波动越来越小,即钉尖朝上的频率具有稳定性。
(3)根据上表完成下面的折线统计图:
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
20
由上图可知,随着试验次数越来越大,钉尖朝上的频率越来越接近0.6,且波动越来越小,即钉尖朝上的频率具有稳定性。
如图显示了用计算机模拟随机投掷一枚图钉的n次试验的结果。
结论:在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性。
议一议:
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)两位同学一起做了1000次掷图钉的试验,其中有640次钉尖朝上。据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大。你同意他们的说法吗?
1、在试验次数很大时,随机事件发生的频率具有稳定性。
2、探究可能性问题的过程:
人们在长期的实践中发现,在随机试验中, 由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小。
练习1、某射击运动员在同一条件下进行射击,结果如下表所示:
(1)完成上表;
(2)根据上表画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
0.9
0.8
0.82
0.88
0.84
0.858
0.861
击中靶心的频率=击中靶心的次数÷射击总次数
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率m/n
(2)根据上表画出该运动员击中靶心的频率的折线统计图;
(3)答:随着射击总次数的增加,击中靶心的频率越来越接近0.86,且趋于稳定。
(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
0.9
0.8
0.82
0.88
0.84
0.858
0.861
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率m/n
练习2、某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法?
在同样条件下,大量地对这种幼树进行移植并统计成活情况,计算成活的频率.如果随着移植棵数的越来越大,频率越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值。
0.8
0.923
8073
练习2、(1)下表是统计试验中的部分数据,请补充完整:
(2)由下表可以发现,幼树移植成活的频率在____左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
0.9
(3)林业部门种植了该幼树1000棵,估计能成活
_______棵.
(4)我们学校需种植这样的树苗500棵来绿化校
园,则至少向林业部门购买约_______棵.
900
556
(3)1000×0.9=900(棵)
(4)500÷0.9≈556 (棵)
47
8÷10
50×0.94
成活数÷移植总数=成活的频率
移植总数 成活数 成活的频率
10 8
50 0.94
270 235 0.870
400 369
750 662 0.883
1500 1335 0.890
3500 3203 0.915
7000 6335 0.905
9000 0.897
14000 12628 0.902
抛一个如图所示的瓶盖,盖口向上或盖口向下的可能性是否一样大?怎样才能验证自己结论的正确性?
经历了“猜测——试验——收集试验数据——分析试验数据——验证猜测”的过程。
发展数据分析的观念:通过数据分析体验随机性,一方面对于同样的事情每次收集到的数据可能不同,另一方面只要有足够的数据就可能从中发现规律。
1.知识方面
②频率的稳定性:当试验次数很大时,事件的频率会在一个常数附近摆动,即频率具有稳定性。
2、过程与方法
3.核心素养
3、对某批产品的质量进行随机抽查,结果如下表所示:
(1)完成上表;
(2)根据上表,画出产品合格率变化的折线统计图;
(3)观察画出的折线统计图,产品合格率的变化有什么规律?
1.在对1000件产品进行检测后,发现了4件次品,则检测到次品的频率是( )
A. B. C. D.0
当堂检测:
2.某种绿豆在相同条件下的发芽试验结果如表,根据表中数据我们会发现当参与试验的这种绿豆的粒数很大时,它的发芽率会在一个常数_________附近摆动,即这种绿豆的发芽率具有__________.
每批粒数n 2 5 10 50 100 500 1000 1500
发芽的粒数m 2 4 9 44 92 463 928 1396
发芽的频率 1 0.8 0.9 0.88 0.92 0.926 0.928 0.931
随机抽取的产品数n 10 20 50 100 200 500 1000
合格的产品数m 9 19 47 93 187 467 935
合格率m/n
3、对某批产品的质量进行随机抽查,结果如下表所示:
(1)完成上表;
(2)根据上表,画出产品合格率变化的折线统计图;
(3)观察画出的折线统计图,产品合格率的变化有什么规律?
1.在对1000件产品进行检测后,发现了4件次品,则检测到次品的频率是( )
A. B. C. D.0
当堂检测:
2.某种绿豆在相同条件下的发芽试验结果如表,根据表中数据我们会发现当参与试验的这种绿豆的粒数很大时,它的发芽率会在一个常数_________附近摆动,即这种绿豆的发芽率具有__________.
C
0.93
稳定性
0.9
0.95
0.94
0.93
0.935
0.934
0.935
(2)略
(3)答:在随机抽取的产品数很大时,合格率会稳定在一个常数的附近。
每批粒数n 2 10 50 100 500 1000 2000 3000
发芽的粒数m 2 9 44 92 463 930 1862 2793
发芽的频率 1 0.9 0.88 0.92 0.926 0.93 0.931 0.931
随机抽取的产品数n 10 20 50 100 200 500 1000
合格的产品数m 9 19 47 93 187 467 935
合格率m/n
初中数学七年级(下)
6.2 频率的稳定性(1)
(1)每人做20次掷图钉游戏,并将数据记录在下表中:
20
12
8
0.6
0.4
试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
(1)以下是20组同学的试验结果:
组号 一组 二组 三组 四组 五组 六组 七组 八组 九组 十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 10 15 12 14 13 12 9 12 9 12
钉尖朝下次数 10 5 8 6 7 8 11 8 11 8
钉尖朝上频率
(钉尖朝上次数/试验总次数) 0.5 0.75 0.6 0.7 0.65 0.6 0.45 0.6 0.45 0.6
钉尖朝下频率
(钉尖朝下次数/试验总次数) 0.5 0.25 0.4 0.3 0.35 0.4 0.55 0.4 0.55 0.4
组号 十一组 十二组 十三组 十四组 十五组 十六组 十七组 十八组 十九组 二十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 14 12 7 10 13 13 16 14 13 10
钉尖朝下次数 6 8 13 6 7 7 4 6 7 10
钉尖朝上频率
(钉尖朝上次数/试验总次数) 0.7 0.6 0.35 0.5 0.65 0.65 0.8 0.7 0.65 0.5
钉尖朝下频率
(钉尖朝下次数/试验总次数) 0.025 0.0125 0.02 0.015 0.0175 0.02 0.0275 0.02 0.0275 0.02
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
10
25
51
0.5
0.625
0.638
76 97 118 144 161 187 217 240
0.633 0.606 0.59 0.6 0.575 0.584 0.603 0.6
试验总次数n 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上次数m
钉尖朝上频率m/n
组号 一组 二组 三组 四组 五组 六组 七组 八组 九组 十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 10 15 12 14 13 12 9 12 9 12
组号 十一组 十二组 十三组 十四组 十五组 十六组 十七组 十八组 十九组 二十组
试验总次数 20 20 20 20 20 20 20 20 20 20
钉尖朝上次数 14 12 7 10 13 13 16 14 13 10
(3)根据上表完成下面的折线统计图:
(3)根据上表完成下面的折线统计图:
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
20
由上图可知,随着试验次数越来越大,钉尖朝上的频率越来越接近0.6,且波动越来越小,即钉尖朝上的频率具有稳定性。
(3)根据上表完成下面的折线统计图:
(4)观察折线统计图,钉尖朝上的频率的变化有什么规律?
20
由上图可知,随着试验次数越来越大,钉尖朝上的频率越来越接近0.6,且波动越来越小,即钉尖朝上的频率具有稳定性。
如图显示了用计算机模拟随机投掷一枚图钉的n次试验的结果。
结论:在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性。
议一议:
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎样想的?
(2)两位同学一起做了1000次掷图钉的试验,其中有640次钉尖朝上。据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大。你同意他们的说法吗?
1、在试验次数很大时,随机事件发生的频率具有稳定性。
2、探究可能性问题的过程:
人们在长期的实践中发现,在随机试验中, 由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.
频率的稳定性是由瑞士数学家雅布·伯努利(1654-1705)最早阐明的,他还提出了由频率可以估计事件发生的可能性大小。
练习1、某射击运动员在同一条件下进行射击,结果如下表所示:
(1)完成上表;
(2)根据上表画出该运动员击中靶心的频率的折线统计图;
(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
0.9
0.8
0.82
0.88
0.84
0.858
0.861
击中靶心的频率=击中靶心的次数÷射击总次数
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率m/n
(2)根据上表画出该运动员击中靶心的频率的折线统计图;
(3)答:随着射击总次数的增加,击中靶心的频率越来越接近0.86,且趋于稳定。
(3)观察画出的折线统计图,击中靶心的频率变化有什么规律?
0.9
0.8
0.82
0.88
0.84
0.858
0.861
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率m/n
练习2、某林业部门要考查某种幼树在一定条件下的移植成活率,应采用什么具体做法?
在同样条件下,大量地对这种幼树进行移植并统计成活情况,计算成活的频率.如果随着移植棵数的越来越大,频率越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值。
0.8
0.923
8073
练习2、(1)下表是统计试验中的部分数据,请补充完整:
(2)由下表可以发现,幼树移植成活的频率在____左右摆动,并且随着移植棵数越来越大,这种规律愈加明显.
0.9
(3)林业部门种植了该幼树1000棵,估计能成活
_______棵.
(4)我们学校需种植这样的树苗500棵来绿化校
园,则至少向林业部门购买约_______棵.
900
556
(3)1000×0.9=900(棵)
(4)500÷0.9≈556 (棵)
47
8÷10
50×0.94
成活数÷移植总数=成活的频率
移植总数 成活数 成活的频率
10 8
50 0.94
270 235 0.870
400 369
750 662 0.883
1500 1335 0.890
3500 3203 0.915
7000 6335 0.905
9000 0.897
14000 12628 0.902
抛一个如图所示的瓶盖,盖口向上或盖口向下的可能性是否一样大?怎样才能验证自己结论的正确性?
经历了“猜测——试验——收集试验数据——分析试验数据——验证猜测”的过程。
发展数据分析的观念:通过数据分析体验随机性,一方面对于同样的事情每次收集到的数据可能不同,另一方面只要有足够的数据就可能从中发现规律。
1.知识方面
②频率的稳定性:当试验次数很大时,事件的频率会在一个常数附近摆动,即频率具有稳定性。
2、过程与方法
3.核心素养
3、对某批产品的质量进行随机抽查,结果如下表所示:
(1)完成上表;
(2)根据上表,画出产品合格率变化的折线统计图;
(3)观察画出的折线统计图,产品合格率的变化有什么规律?
1.在对1000件产品进行检测后,发现了4件次品,则检测到次品的频率是( )
A. B. C. D.0
当堂检测:
2.某种绿豆在相同条件下的发芽试验结果如表,根据表中数据我们会发现当参与试验的这种绿豆的粒数很大时,它的发芽率会在一个常数_________附近摆动,即这种绿豆的发芽率具有__________.
每批粒数n 2 5 10 50 100 500 1000 1500
发芽的粒数m 2 4 9 44 92 463 928 1396
发芽的频率 1 0.8 0.9 0.88 0.92 0.926 0.928 0.931
随机抽取的产品数n 10 20 50 100 200 500 1000
合格的产品数m 9 19 47 93 187 467 935
合格率m/n
3、对某批产品的质量进行随机抽查,结果如下表所示:
(1)完成上表;
(2)根据上表,画出产品合格率变化的折线统计图;
(3)观察画出的折线统计图,产品合格率的变化有什么规律?
1.在对1000件产品进行检测后,发现了4件次品,则检测到次品的频率是( )
A. B. C. D.0
当堂检测:
2.某种绿豆在相同条件下的发芽试验结果如表,根据表中数据我们会发现当参与试验的这种绿豆的粒数很大时,它的发芽率会在一个常数_________附近摆动,即这种绿豆的发芽率具有__________.
C
0.93
稳定性
0.9
0.95
0.94
0.93
0.935
0.934
0.935
(2)略
(3)答:在随机抽取的产品数很大时,合格率会稳定在一个常数的附近。
每批粒数n 2 10 50 100 500 1000 2000 3000
发芽的粒数m 2 9 44 92 463 930 1862 2793
发芽的频率 1 0.9 0.88 0.92 0.926 0.93 0.931 0.931
随机抽取的产品数n 10 20 50 100 200 500 1000
合格的产品数m 9 19 47 93 187 467 935
合格率m/n
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
