北师大版七年级下册数学6.3 等可能事件的概率(1)课件(24张ppt)
文档属性
| 名称 | 北师大版七年级下册数学6.3 等可能事件的概率(1)课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 903.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 06:54:01 | ||
图片预览







文档简介
(共24张PPT)
6.3 等可能事件的概率(1)
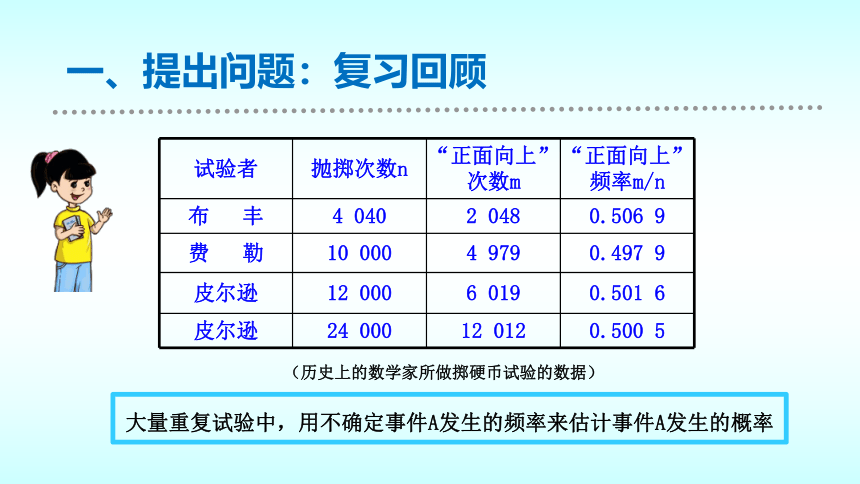
一、提出问题:复习回顾
试验者 抛掷次数n “正面向上”次数m “正面向上”频率m/n
布 丰 4 040 2 048 0.506 9
费 勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
大量重复试验中,用不确定事件A发生的频率来估计事件A发生的概率
(历史上的数学家所做掷硬币试验的数据)
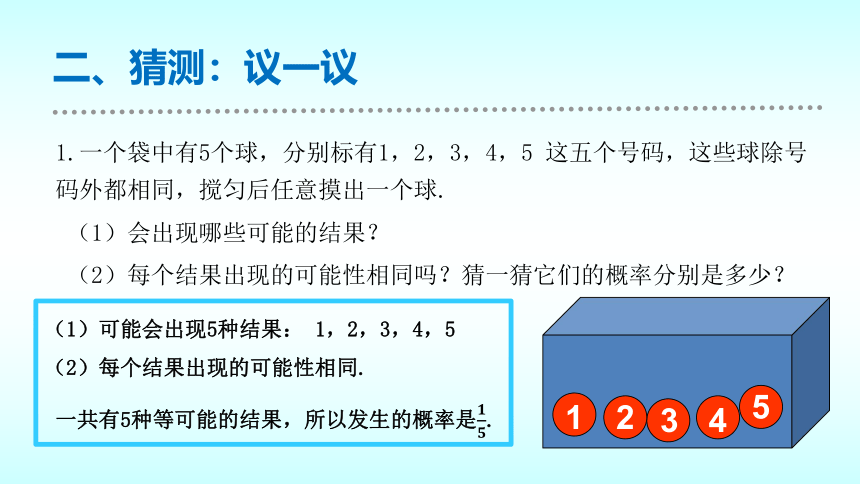
二、猜测:议一议
1.一个袋中有5个球,分别标有1,2,3,4,5 这五个号码,这些球除号码外都相同,搅匀后任意摸出一个球.
(1)会出现哪些可能的结果?
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
4
3
5
1
2
(1)可能会出现5种结果: 1,2,3,4,5
(2)每个结果出现的可能性相同.
一共有5种等可能的结果,所以发生的概率是.
2.前面我们提到的掷硬币、掷骰子和摸球的游戏有什么共同的特点?
二、猜测:议一议
按下暂停键,自己想一想
2.前面我们提到的掷硬币、掷骰子和摸球的游戏有什么共同的特点?
每个结果出现的可能性相同.
所有可能的结果有有限种.
【有限性】
【等可能性】
二、猜测:议一议
每一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
古典概型两基本特点:有限性、等可能性.
这个试验就称为古典概型.
二、猜测:形成共识
下列试验中,哪些结果是等可能的试验?
三、思考交流:想一想
①掷硬币
③发芽试验中的“发芽”与“不发芽”
⑥掷一枚图钉
②射击试验中的“中靶”与“脱靶”
⑤掷骰子
④摸牌
你还能举例一些等可能的试验吗?
古典概型两基本特点:有限性、等可能性.
四、抽象概括:提出概念
一般地,如果一个试验有n个等可能的结果,事件A包含其中的m个结果,那么事件A发生的概率为:
古典概型两基本特点:有限性、等可能性.
五、解决问题:例题精讲
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚质地均匀的骰子,掷出的点数分别是1,2,3,4,5,6,所有可能的结果有6种:因为骰子是质地均匀的,所以每种结果出现的可能性相等.
古典概型两基本特点:有限性、等可能性.
按下暂停键,自己做一做
(1)掷出的点数大于4的结果分别是5,6.
∴点数大于4的结果只有2种;
∴ P(掷出的点数大于4)= =
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
五、解决问题:例题精讲
(2)掷出的点数是偶数的分别是2,4,6;
∴掷出的点数是偶数的结果有3种;
∴ P(掷出的点数是偶数)= = .
【方法总结】
概率的求法关键是找准两点:
①符合条件的情况数目;②全部情况的总数.
二者的比值就是其发生的概率.
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
五、解决问题:例题精讲
六、随堂练习
1、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中.搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
2、一副扑克牌,任意抽取其中的一张,
(1)抽到方块的概率是多少?
(2)从概率的角度解释一下,打牌的时候,你摸到大王的机会比摸到3的机会小.
按下暂停键,自己做一做
六、随堂练习
1、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中.搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
解:出现A,B,C,D,E五种结果,他们是等可能的.
古典概型两基本特点:有限性、等可能性.
2、一副扑克牌,任意抽取其中的一张,
(1)抽到方块的概率是多少?
(2)从概率的角度解释一下,打牌的时候,
你摸到大王的机会比摸到3的机会小.
六、随堂练习
解: (1) P(抽到方块)=
(2)∵ P(摸到大王)= , P(摸到3)=
∴ P(摸到大王)<P(摸到3)
∴摸到大王的机会比摸到3的机会小.
概率是描述不确定现象的数学模型.
七、课堂小结
1、知识上:
2、思想方法上:
解决问题的过程:提出问题-猜测-思考交流-抽象概括-解决问题.
概率是描述不确定现象的数学模型.
古典概型的特点:有限性、等可能性.
按下暂停键,自己想一想
1、任意掷一枚质地均匀的骰子.
(1)掷出的点数小于4的概率是多少?(2)掷出的点数是奇数的概率是多少?
(3)掷出的点数是7的概率是多少? (4)掷出的点数小于7的概率是多少?
八、当堂检测
2、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?
3、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
按下暂停键,自己做一做
1、任意掷一枚质地均匀的骰子.
(1)掷出的点数小于4的概率是多少?
(2)掷出的点数是奇数的概率是多少?
(3)掷出的点数是7的概率是多少?
(4)掷出的点数小于7的概率是多少?
P(点数小于4)= =
P(点数是奇数)= =
P(点数是7)= =
P(点数小于7)= =
(1)点数小于4的情况有1,2,3.
(2)点数是奇数的情况有1,3,5.
(3)点数是7的情况不存在.
(4)点数小于7的情况有1,2,3,4,5,6.
八、当堂检测
2、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?
P(答对题)=
解: A、B、C、D四个答案中只有1个是正确的.
八、当堂检测
3、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
P(标有数字3)=
P(标有数字1)=
P(标有数字为奇数)=
数字为奇数的有:1,1,3,5.共计4种情况.
八、当堂检测
4、小明所在的班有40名同学,从中选出一名同学为家长会准备工作.请你设计一种方案,使每一名同学被选中的概率相同.
九、问题解决
将40名同学的名字分别写在40张纸签上,随机抽取一张,抽出写有谁的名字的纸签就选中谁.
将数字1-40写在40张纸签上,让每个同学随机抽取一张,选取一个数字为最终抽中结果.
按下暂停键,自己做一做
十、自我检测
A组:
1.九张同样的卡片分别写有数字-4,-3,-2,-1,0,1,2,3,4,任意抽取一张,所抽卡片上数字的绝对值小于2的概率是 ( ).
A. B. C. D.
2.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到的卡片上算式正确的概率是 ( ).
A. B. C. D.1
a3·a4=a7
a8÷a4=a2
a2+a3=2a5
(a3)2=a6
按下暂停键,自己做一做
十、自我检测
B组:3.合作小组的4位同学坐在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则学生B坐在2号座位的概率是 .
C组:4.有一组互不全等的三角形,它们的三边长均为整数,每个三角形有两条边的长分别为5和7.
(1)请写出其中一个三角形的第三边的长.
(2)设组中最多有n个三角形,求n的值.
(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.
按下暂停键,自己做一做
1.【解析】选B.卡片中一共有9个数字,其中绝对值小于2的数字共有3个:-1,0,1,所以任意抽取一张,所抽卡片上数字的绝对值小于2的概率是=.
2.【解析】选B.四张卡片中第一张和第三张是正确的,随机抽取一张,抽到的卡片上算式正确的概率是=.
3.【解析】学生B可以坐在1,2,3号三个位置,且坐在每个位置的可能性相等,因此他坐在2号位置的概率是.答案:.
4.【解析】(1)第三边长取3(2到12之间任意整数均可,不包括2,12).
(2)设第三边长为x,7-5x=3,4,5,6,7,8,9,10,11,n=9.
(3)当n=9时,周长要为偶数,5+7=12为偶数,所以只需第三边为偶数,所以此时x=4,6,8,10, P(偶数)=.
自我检测参考答案
6.3 等可能事件的概率(1)
一、提出问题:复习回顾
试验者 抛掷次数n “正面向上”次数m “正面向上”频率m/n
布 丰 4 040 2 048 0.506 9
费 勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
大量重复试验中,用不确定事件A发生的频率来估计事件A发生的概率
(历史上的数学家所做掷硬币试验的数据)
二、猜测:议一议
1.一个袋中有5个球,分别标有1,2,3,4,5 这五个号码,这些球除号码外都相同,搅匀后任意摸出一个球.
(1)会出现哪些可能的结果?
(2)每个结果出现的可能性相同吗?猜一猜它们的概率分别是多少?
4
3
5
1
2
(1)可能会出现5种结果: 1,2,3,4,5
(2)每个结果出现的可能性相同.
一共有5种等可能的结果,所以发生的概率是.
2.前面我们提到的掷硬币、掷骰子和摸球的游戏有什么共同的特点?
二、猜测:议一议
按下暂停键,自己想一想
2.前面我们提到的掷硬币、掷骰子和摸球的游戏有什么共同的特点?
每个结果出现的可能性相同.
所有可能的结果有有限种.
【有限性】
【等可能性】
二、猜测:议一议
每一个试验的所有可能的结果有n种,每次试验有且只有其中的一种结果出现.如果每种结果出现的可能性相同,那么我们就称这个试验的结果是等可能的.
古典概型两基本特点:有限性、等可能性.
这个试验就称为古典概型.
二、猜测:形成共识
下列试验中,哪些结果是等可能的试验?
三、思考交流:想一想
①掷硬币
③发芽试验中的“发芽”与“不发芽”
⑥掷一枚图钉
②射击试验中的“中靶”与“脱靶”
⑤掷骰子
④摸牌
你还能举例一些等可能的试验吗?
古典概型两基本特点:有限性、等可能性.
四、抽象概括:提出概念
一般地,如果一个试验有n个等可能的结果,事件A包含其中的m个结果,那么事件A发生的概率为:
古典概型两基本特点:有限性、等可能性.
五、解决问题:例题精讲
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
解:任意掷一枚质地均匀的骰子,掷出的点数分别是1,2,3,4,5,6,所有可能的结果有6种:因为骰子是质地均匀的,所以每种结果出现的可能性相等.
古典概型两基本特点:有限性、等可能性.
按下暂停键,自己做一做
(1)掷出的点数大于4的结果分别是5,6.
∴点数大于4的结果只有2种;
∴ P(掷出的点数大于4)= =
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
五、解决问题:例题精讲
(2)掷出的点数是偶数的分别是2,4,6;
∴掷出的点数是偶数的结果有3种;
∴ P(掷出的点数是偶数)= = .
【方法总结】
概率的求法关键是找准两点:
①符合条件的情况数目;②全部情况的总数.
二者的比值就是其发生的概率.
例1 任意掷一枚质地均匀骰子.
(1)掷出的点数大于4的概率是多少?
(2)掷出的点数是偶数的概率是多少?
五、解决问题:例题精讲
六、随堂练习
1、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中.搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
2、一副扑克牌,任意抽取其中的一张,
(1)抽到方块的概率是多少?
(2)从概率的角度解释一下,打牌的时候,你摸到大王的机会比摸到3的机会小.
按下暂停键,自己做一做
六、随堂练习
1、将A,B,C,D,E这五个字母分别写在5张同样的纸条上,并将这些纸条放在一个盒子中.搅匀后从中任意摸出一张,会出现哪些可能的结果?它们是等可能的吗?
解:出现A,B,C,D,E五种结果,他们是等可能的.
古典概型两基本特点:有限性、等可能性.
2、一副扑克牌,任意抽取其中的一张,
(1)抽到方块的概率是多少?
(2)从概率的角度解释一下,打牌的时候,
你摸到大王的机会比摸到3的机会小.
六、随堂练习
解: (1) P(抽到方块)=
(2)∵ P(摸到大王)= , P(摸到3)=
∴ P(摸到大王)<P(摸到3)
∴摸到大王的机会比摸到3的机会小.
概率是描述不确定现象的数学模型.
七、课堂小结
1、知识上:
2、思想方法上:
解决问题的过程:提出问题-猜测-思考交流-抽象概括-解决问题.
概率是描述不确定现象的数学模型.
古典概型的特点:有限性、等可能性.
按下暂停键,自己想一想
1、任意掷一枚质地均匀的骰子.
(1)掷出的点数小于4的概率是多少?(2)掷出的点数是奇数的概率是多少?
(3)掷出的点数是7的概率是多少? (4)掷出的点数小于7的概率是多少?
八、当堂检测
2、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?
3、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
按下暂停键,自己做一做
1、任意掷一枚质地均匀的骰子.
(1)掷出的点数小于4的概率是多少?
(2)掷出的点数是奇数的概率是多少?
(3)掷出的点数是7的概率是多少?
(4)掷出的点数小于7的概率是多少?
P(点数小于4)= =
P(点数是奇数)= =
P(点数是7)= =
P(点数小于7)= =
(1)点数小于4的情况有1,2,3.
(2)点数是奇数的情况有1,3,5.
(3)点数是7的情况不存在.
(4)点数小于7的情况有1,2,3,4,5,6.
八、当堂检测
2、一道单选题有A、B、C、D四个备选答案,当你不会做时,从中随机选一个答案,你答对的概率是多少?
P(答对题)=
解: A、B、C、D四个答案中只有1个是正确的.
八、当堂检测
3、有7张纸签,分别标有数字1,1,2,2,3,4,5,从中随机地抽出一张,求:
(1)抽出标有数字3的纸签的概率;
(2)抽出标有数字1的纸签的概率;
(3)抽出标有数字为奇数的纸签的概率.
P(标有数字3)=
P(标有数字1)=
P(标有数字为奇数)=
数字为奇数的有:1,1,3,5.共计4种情况.
八、当堂检测
4、小明所在的班有40名同学,从中选出一名同学为家长会准备工作.请你设计一种方案,使每一名同学被选中的概率相同.
九、问题解决
将40名同学的名字分别写在40张纸签上,随机抽取一张,抽出写有谁的名字的纸签就选中谁.
将数字1-40写在40张纸签上,让每个同学随机抽取一张,选取一个数字为最终抽中结果.
按下暂停键,自己做一做
十、自我检测
A组:
1.九张同样的卡片分别写有数字-4,-3,-2,-1,0,1,2,3,4,任意抽取一张,所抽卡片上数字的绝对值小于2的概率是 ( ).
A. B. C. D.
2.如图,有四张不透明的卡片除正面的算式不同外,其余完全相同,将它们背面朝上洗匀后,从中随机抽取一张,则抽到的卡片上算式正确的概率是 ( ).
A. B. C. D.1
a3·a4=a7
a8÷a4=a2
a2+a3=2a5
(a3)2=a6
按下暂停键,自己做一做
十、自我检测
B组:3.合作小组的4位同学坐在课桌旁讨论问题,学生A的座位如图所示,学生B,C,D随机坐到其他三个座位上,则学生B坐在2号座位的概率是 .
C组:4.有一组互不全等的三角形,它们的三边长均为整数,每个三角形有两条边的长分别为5和7.
(1)请写出其中一个三角形的第三边的长.
(2)设组中最多有n个三角形,求n的值.
(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.
按下暂停键,自己做一做
1.【解析】选B.卡片中一共有9个数字,其中绝对值小于2的数字共有3个:-1,0,1,所以任意抽取一张,所抽卡片上数字的绝对值小于2的概率是=.
2.【解析】选B.四张卡片中第一张和第三张是正确的,随机抽取一张,抽到的卡片上算式正确的概率是=.
3.【解析】学生B可以坐在1,2,3号三个位置,且坐在每个位置的可能性相等,因此他坐在2号位置的概率是.答案:.
4.【解析】(1)第三边长取3(2到12之间任意整数均可,不包括2,12).
(2)设第三边长为x,7-5
(3)当n=9时,周长要为偶数,5+7=12为偶数,所以只需第三边为偶数,所以此时x=4,6,8,10, P(偶数)=.
自我检测参考答案
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
