五年级下册数学一课一练-2.3长方体的表面积(含答案)
文档属性
| 名称 | 五年级下册数学一课一练-2.3长方体的表面积(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 06:27:19 | ||
图片预览



文档简介
五年级下册数学一课一练-2.3长方体的表面积
一、单选题
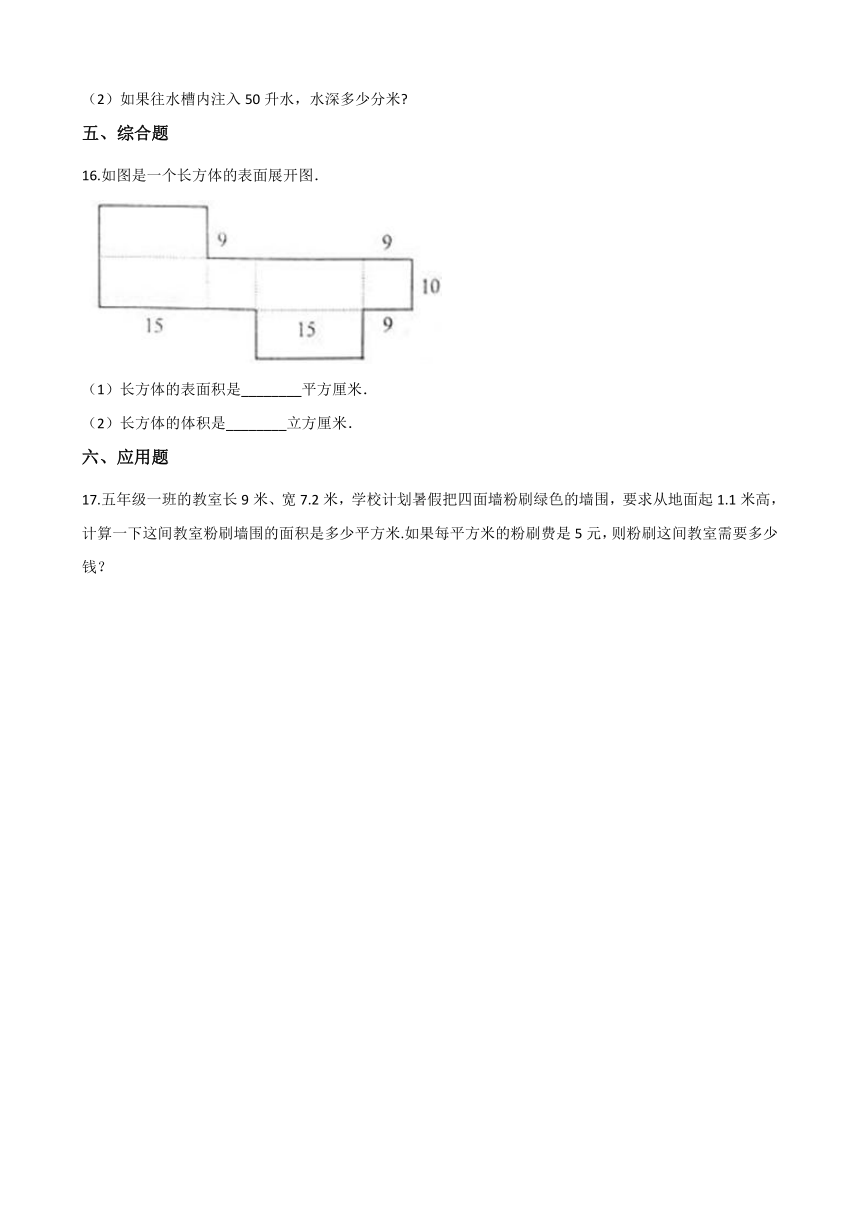
1.长方体底面的面积是(? ???)cm2。
A.?20????????????????????????????????????????????B.?12????????????????????????????????????????????C.?15
2.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2。原来长方体木料的表面积是(??? )cm。
A.?64???????????????????????????????????????B.?128???????????????????????????????????????C.?160???????????????????????????????????????D.?320
3.把一根长2m的长方体木材平均截成3段,表面积增加了100dm2 , 原来木材体积是(??? )dm3.
A.?50??????????????????????????????????????B.?100??????????????????????????????????????C.?500??????????????????????????????????????D.?1000
4.把一个表面积是50cm2的长方体,按如图切三刀分成8个小长方体,表面积比原来增加了(?? )cm2 .
A.?10????????????????????????????????????????B.?25????????????????????????????????????????C.?50????????????????????????????????????????D.?100
二、判断题
5.棱长6厘米的正方体表面积与体积相等。
6.棱长为6分米的正方体,它的表面积和体积相等.
7.当正方体的棱长是6米时,它的表面积和体积相等.
8.一个正方体锯成两个完全相等的长方体,每个长方体的表面积是正方体的 。
三、填空题
9.长方体的棱长总和是120厘米.长方体的宽是10厘米,高是8厘米.
(1)这个长方体的长是________厘米.
(2)这个长方体上、下两个面的面积一共是________平方厘米.
(3)这个长方体前后两个面的面积是________平方厘米.
(4)这个长方体的两个侧面的面积是________平方厘米.
(5)这个长方体的表面积是________平方厘米.
10.长方体或正方体的表面积是指长方体或正方体________的和.
11.一个长方体的棱长总和是120厘米,长、宽、高的比是3:2:5。这个长方体的表面积是________平方厘米,体积是________立方厘米。
12.一种纸袋(如下图)打开后的形状是长方体,长55厘米,宽8厘米,高40厘米.做这个纸袋________需要多少硬纸。这个纸袋可以盛________立方厘米的物体。
13.一个长方体木块,高2.4cm,平行于底面截成两个长方体后,表面积比原来增加了100cm2。原长方体木料的体积是________?cm3。
四、解答题
14.希望小学有一间长10米、宽6米、高3.5米的长方体教室。
(1)这间教室的空间有多大?
(2)现在要在教室四面墙壁贴1.2米高的瓷砖,扣除门、窗、黑板面积6平方米,这间教室贴瓷砖的面积是多少平方米?
15.一个长方体无盖铁皮水槽,长和宽都是5分米,高是8分米。
(1)做这个水槽至少需要多少铁皮?
(2)如果往水槽内注入50升水,水深多少分米?
五、综合题
16.如图是一个长方体的表面展开图.
(1)长方体的表面积是________平方厘米.
(2)长方体的体积是________立方厘米.
六、应用题
17.五年级一班的教室长9米、宽7.2米,学校计划暑假把四面墙粉刷绿色的墙围,要求从地面起1.1米高,计算一下这间教室粉刷墙围的面积是多少平方米.如果每平方米的粉刷费是5元,则粉刷这间教室需要多少钱?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】5×3=15(cm2). 故答案为:C. 【分析】根据题意,要求长方体的底面的面积,用长×宽=长方体的底面的面积,据此列式解答.
2.【答案】 C
【解析】【解答】32÷2=16(cm2) 16×6×2-32 =96×2-32 =192-32 =160(cm2) 故答案为:C
【分析】 沿虚线把长方体木料刚好锯成2个同样的正方体, 表面积比原长方体增加了32cm2。 这时增加了两个正方形的面,?这两个正方形的面积是32cm2。求出一个正方形的面积后,用“这个正方形的面积×6=一个正方体的表面积”,“这个正方体的表面积×2-32cm2=长方体的表面积”。
3.【答案】 C
【解析】【解答】100÷4=25(dm2), 2m=20dm, 25×20=500(dm3)。 故答案为:C。 【分析】根据题意可知,将一根长2m的长方体木材平均截成3段,表面积增加了4个底面积,用增加的表面积÷4=底面积,再把2m化成20dm,最后用底面积×高=长方体的体积,据此列式解答。
4.【答案】 C
【解析】【解答】把一个表面积是50cm2的长方体,按如图切三刀分成8个小长方体,表面积增加的部分正好是一个长方体的表面积,故表面积增加了50cm2。 故答案为:C 【分析】与上下面平行的一刀,切开了两个面正好等于上下两面的面积;与前后面平行的一刀,切开的两个面正好等于前后两个面的面积;与左右两个面平行的一刀,切开的两个面正好是左右两个面的面积。故增加的面正好是长方体的上下、前后、左右,六个面,故增加的面积等于原长方体的表面积。
二、判断题
5.【答案】错误
【解析】【解答】解:棱长6厘米的正方体表面积和体积不相等,原题说法错误。 故答案为:错误。
【分析】表面积和体积的意义不同,无法比较大小,因此正方体表面积与体积是不可能相等的。
6.【答案】 错误
【解析】【解答】单位不一样,不能比较大小,本题错。 故答案为:错误。 【分析】表面积是面积单位,体积是体积单位,不是相同单位的,无法进行比较。
7.【答案】 错误
【解析】【解答】解:表面积和体积的意义不同,无法比较大小。原题说法错误。 故答案为:错误
【分析】正方体表面积是表面6个面的面积之和,正方体的体积是所占空间的大小,表面积和体积的意义不同,无法比较大小。
8.【答案】 错误
【解析】【解答】 一个正方体锯成两个完全相等的长方体,每个长方体的表面积是正方体的加上一个正方体的面的面积,原题说法错误。 故答案为:错误。 【分析】 此题主要考查了长方体和正方体表面积的认识,把一个正方体锯成两个完全相等的长方体后,表面积比原来增加了两个正方体的面的面积,所以每个长方体的表面积是原来的正方体的表面积的一半加上一个正方体的面的面积,据此判断。
三、填空题
9.【答案】 (1)12 (2)240 (3)192 (4)160 (5)592
【解析】【解答】(1)10x4+8x4=72(厘米)120–72=48(厘米)48÷4=12(厘米);(2)12x10x2=240(平方厘米)? (3)12x8x2=192(平方厘米);(4)10x8x2=160(平方厘米);(5)240+192+160=592(平方厘米)? ? ? ? ? ? ? ? ? ? ? ? ?
【分析】(1)长方体有12条棱,4条长,4条宽,4条高。故填:12。 (2)长方体上下面是面积相等的2个长方形,长12厘米,宽10厘米。故填:240. (3)长方体前后面是面积相等的2个长方形,长12厘米,宽(高)8厘米。故填:192。 (4)长方体侧面是面积相等的2个长方形,长(宽)10厘米,宽(高)8厘米。故填:160。 (5)长方体的表面有6个面组成,上下2个面,前后2个面,2个侧面。故填:592.
10.【答案】 六个面面积
【解析】【解答】长方体或正方体都是有6个面组成,长方体相对的面面积相等,有3组相对面;正方体6个面面积都相等,因此长方体或正方体的表面的面积即表面积就是6个面面积的和。故填六个面面积。
【分析】根据正方体长方体的特征进行解答
11.【答案】 558;810
【解析】【解答】120÷4=30(厘米) 30÷(3+2+5) =30÷10 =3(厘米) 3×3=9(厘米) 3×2=6(厘米) 3×5=15(厘米) (9×6+9×15+6×15)×2 =(54+135+90)×2 =279×2 =558(平方厘米) 9×6×15 =54×15 =810(立方厘米) 故答案为:558;810。 【分析】首先,棱长和÷4=一组棱长的和(长、宽和高的和);然后,一组棱长和÷长宽高的份数和=一份的长度,分别用“一份的长度”乘以长、宽和高所占的分数,求出长、宽和高的长度;最后根据长方体的表面积公式和体积公式求出它的表面和体积。长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高。
12.【答案】 5480平方厘米;17600
【解析】【解答】(55×40+8×40)×2+55×8 =(2200+320)×2+55×8 =2520×2+55×8 =5040+440 =5480(平方厘米) 55×8×40 =440×40 =17600(立方厘米) 故答案为:5480平方厘米;17600.
【分析】根据题意可知,已知长方体纸袋的长、宽、高,要求无盖长方体纸袋的表面积,用公式:无盖长方体的表面积=(长×高+宽×高)×2+长×宽,要求长方体的体积,用公式:长方体的体积=长×宽×高,据此解答.
13.【答案】 120
【解析】【解答】100÷2×2.4 =50×2.4 =120(cm3) 故答案为:120。 【分析】根据条件“ 平行于底面截成两个长方体后,表面积比原来增加了100cm2 ”可知,增加了两个底面积,用增加的表面积÷2=长方体的底面积,然后用长方体的底面积×高=长方体的体积,据此列式解答。
四、解答题
14.【答案】 (1)解:10×6×3.5=210(平方米)
答:这间教室的空间有210平方米。
(2)解:(10×1.2+6×1.2)×2-6=38.4-6=32.4(平方米)
答:这间教室贴瓷砖的面积是32.4平方米。
【解析】【分析】(1)求这间教室的空间有多大就是求教室的体积;教室的体积=教室的长×宽×高; (2)(教室的长×瓷砖的高+教室的宽×瓷砖的高)×2=教室四周一圈四个面的面积;教室四周一圈四个面的面积- 门、窗、黑板面积=贴瓷砖的面积。
15.【答案】 (1)解:5×5+5×8×4=185(平方分米)
答:做这个水槽至少需要185平方分米铁皮。
(2)解:50÷(5×5)=2(分米)
答:水深2分米。
【解析】【分析】(1)因为这是一个无盖的水箱,所以制作时少去1个“长×卷”这个面,而且这个长方体水槽有两个面那么需要铁皮的平方分米数=长×宽+长×高×4; (2)水的深度=注入水的深度÷底面积,其中底面积=长×宽。
五、综合题
16.【答案】 (1)750 (2)1350
【解析】【解答】(1)(15×10+15×9+10×9)×2 =(150+135+90)×2 =375×2 =750(平方厘米) (2)15×10×9 =150×9 =1350(立方厘米) 故答案为:(1)750;(2)1350。
【分析】由同一个顶点引出的三条边分别为长方体的长、宽、高。根据长方体的展开图可知,长方体的长、宽、高分别为:15厘米、10厘米=9厘米。 (1)长方体的表面积=(长×宽+长×高+宽×高)×2; (2)长方体的体积=长×宽×高。
六、应用题
17.【答案】 解:(9×1.1+7.2×1.1)×2=35.64(平方米),35.64×5=178.2(元)
【解析】【解答】(9×1.1+7.2×1.1)×2 =(9.9+7.92)×2 =17.82×2 =35.64(平方米) 35.64×5=178.2(元). 答:这间教室粉刷墙围的面积是35.64平方米,粉刷这间教室需要178.2元.
【分析】根据题意可知,要求粉刷的墙围面积,用(粉刷的长度×高度+粉刷的宽度×高度)×2=粉刷的四面墙围的面积; 然后用每平方米的粉刷费用×粉刷的面积=粉刷这间教室的总费用,据此列式解答.
一、单选题
1.长方体底面的面积是(? ???)cm2。
A.?20????????????????????????????????????????????B.?12????????????????????????????????????????????C.?15
2.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2。原来长方体木料的表面积是(??? )cm。
A.?64???????????????????????????????????????B.?128???????????????????????????????????????C.?160???????????????????????????????????????D.?320
3.把一根长2m的长方体木材平均截成3段,表面积增加了100dm2 , 原来木材体积是(??? )dm3.
A.?50??????????????????????????????????????B.?100??????????????????????????????????????C.?500??????????????????????????????????????D.?1000
4.把一个表面积是50cm2的长方体,按如图切三刀分成8个小长方体,表面积比原来增加了(?? )cm2 .
A.?10????????????????????????????????????????B.?25????????????????????????????????????????C.?50????????????????????????????????????????D.?100
二、判断题
5.棱长6厘米的正方体表面积与体积相等。
6.棱长为6分米的正方体,它的表面积和体积相等.
7.当正方体的棱长是6米时,它的表面积和体积相等.
8.一个正方体锯成两个完全相等的长方体,每个长方体的表面积是正方体的 。
三、填空题
9.长方体的棱长总和是120厘米.长方体的宽是10厘米,高是8厘米.
(1)这个长方体的长是________厘米.
(2)这个长方体上、下两个面的面积一共是________平方厘米.
(3)这个长方体前后两个面的面积是________平方厘米.
(4)这个长方体的两个侧面的面积是________平方厘米.
(5)这个长方体的表面积是________平方厘米.
10.长方体或正方体的表面积是指长方体或正方体________的和.
11.一个长方体的棱长总和是120厘米,长、宽、高的比是3:2:5。这个长方体的表面积是________平方厘米,体积是________立方厘米。
12.一种纸袋(如下图)打开后的形状是长方体,长55厘米,宽8厘米,高40厘米.做这个纸袋________需要多少硬纸。这个纸袋可以盛________立方厘米的物体。
13.一个长方体木块,高2.4cm,平行于底面截成两个长方体后,表面积比原来增加了100cm2。原长方体木料的体积是________?cm3。
四、解答题
14.希望小学有一间长10米、宽6米、高3.5米的长方体教室。
(1)这间教室的空间有多大?
(2)现在要在教室四面墙壁贴1.2米高的瓷砖,扣除门、窗、黑板面积6平方米,这间教室贴瓷砖的面积是多少平方米?
15.一个长方体无盖铁皮水槽,长和宽都是5分米,高是8分米。
(1)做这个水槽至少需要多少铁皮?
(2)如果往水槽内注入50升水,水深多少分米?
五、综合题
16.如图是一个长方体的表面展开图.
(1)长方体的表面积是________平方厘米.
(2)长方体的体积是________立方厘米.
六、应用题
17.五年级一班的教室长9米、宽7.2米,学校计划暑假把四面墙粉刷绿色的墙围,要求从地面起1.1米高,计算一下这间教室粉刷墙围的面积是多少平方米.如果每平方米的粉刷费是5元,则粉刷这间教室需要多少钱?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】5×3=15(cm2). 故答案为:C. 【分析】根据题意,要求长方体的底面的面积,用长×宽=长方体的底面的面积,据此列式解答.
2.【答案】 C
【解析】【解答】32÷2=16(cm2) 16×6×2-32 =96×2-32 =192-32 =160(cm2) 故答案为:C
【分析】 沿虚线把长方体木料刚好锯成2个同样的正方体, 表面积比原长方体增加了32cm2。 这时增加了两个正方形的面,?这两个正方形的面积是32cm2。求出一个正方形的面积后,用“这个正方形的面积×6=一个正方体的表面积”,“这个正方体的表面积×2-32cm2=长方体的表面积”。
3.【答案】 C
【解析】【解答】100÷4=25(dm2), 2m=20dm, 25×20=500(dm3)。 故答案为:C。 【分析】根据题意可知,将一根长2m的长方体木材平均截成3段,表面积增加了4个底面积,用增加的表面积÷4=底面积,再把2m化成20dm,最后用底面积×高=长方体的体积,据此列式解答。
4.【答案】 C
【解析】【解答】把一个表面积是50cm2的长方体,按如图切三刀分成8个小长方体,表面积增加的部分正好是一个长方体的表面积,故表面积增加了50cm2。 故答案为:C 【分析】与上下面平行的一刀,切开了两个面正好等于上下两面的面积;与前后面平行的一刀,切开的两个面正好等于前后两个面的面积;与左右两个面平行的一刀,切开的两个面正好是左右两个面的面积。故增加的面正好是长方体的上下、前后、左右,六个面,故增加的面积等于原长方体的表面积。
二、判断题
5.【答案】错误
【解析】【解答】解:棱长6厘米的正方体表面积和体积不相等,原题说法错误。 故答案为:错误。
【分析】表面积和体积的意义不同,无法比较大小,因此正方体表面积与体积是不可能相等的。
6.【答案】 错误
【解析】【解答】单位不一样,不能比较大小,本题错。 故答案为:错误。 【分析】表面积是面积单位,体积是体积单位,不是相同单位的,无法进行比较。
7.【答案】 错误
【解析】【解答】解:表面积和体积的意义不同,无法比较大小。原题说法错误。 故答案为:错误
【分析】正方体表面积是表面6个面的面积之和,正方体的体积是所占空间的大小,表面积和体积的意义不同,无法比较大小。
8.【答案】 错误
【解析】【解答】 一个正方体锯成两个完全相等的长方体,每个长方体的表面积是正方体的加上一个正方体的面的面积,原题说法错误。 故答案为:错误。 【分析】 此题主要考查了长方体和正方体表面积的认识,把一个正方体锯成两个完全相等的长方体后,表面积比原来增加了两个正方体的面的面积,所以每个长方体的表面积是原来的正方体的表面积的一半加上一个正方体的面的面积,据此判断。
三、填空题
9.【答案】 (1)12 (2)240 (3)192 (4)160 (5)592
【解析】【解答】(1)10x4+8x4=72(厘米)120–72=48(厘米)48÷4=12(厘米);(2)12x10x2=240(平方厘米)? (3)12x8x2=192(平方厘米);(4)10x8x2=160(平方厘米);(5)240+192+160=592(平方厘米)? ? ? ? ? ? ? ? ? ? ? ? ?
【分析】(1)长方体有12条棱,4条长,4条宽,4条高。故填:12。 (2)长方体上下面是面积相等的2个长方形,长12厘米,宽10厘米。故填:240. (3)长方体前后面是面积相等的2个长方形,长12厘米,宽(高)8厘米。故填:192。 (4)长方体侧面是面积相等的2个长方形,长(宽)10厘米,宽(高)8厘米。故填:160。 (5)长方体的表面有6个面组成,上下2个面,前后2个面,2个侧面。故填:592.
10.【答案】 六个面面积
【解析】【解答】长方体或正方体都是有6个面组成,长方体相对的面面积相等,有3组相对面;正方体6个面面积都相等,因此长方体或正方体的表面的面积即表面积就是6个面面积的和。故填六个面面积。
【分析】根据正方体长方体的特征进行解答
11.【答案】 558;810
【解析】【解答】120÷4=30(厘米) 30÷(3+2+5) =30÷10 =3(厘米) 3×3=9(厘米) 3×2=6(厘米) 3×5=15(厘米) (9×6+9×15+6×15)×2 =(54+135+90)×2 =279×2 =558(平方厘米) 9×6×15 =54×15 =810(立方厘米) 故答案为:558;810。 【分析】首先,棱长和÷4=一组棱长的和(长、宽和高的和);然后,一组棱长和÷长宽高的份数和=一份的长度,分别用“一份的长度”乘以长、宽和高所占的分数,求出长、宽和高的长度;最后根据长方体的表面积公式和体积公式求出它的表面和体积。长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高。
12.【答案】 5480平方厘米;17600
【解析】【解答】(55×40+8×40)×2+55×8 =(2200+320)×2+55×8 =2520×2+55×8 =5040+440 =5480(平方厘米) 55×8×40 =440×40 =17600(立方厘米) 故答案为:5480平方厘米;17600.
【分析】根据题意可知,已知长方体纸袋的长、宽、高,要求无盖长方体纸袋的表面积,用公式:无盖长方体的表面积=(长×高+宽×高)×2+长×宽,要求长方体的体积,用公式:长方体的体积=长×宽×高,据此解答.
13.【答案】 120
【解析】【解答】100÷2×2.4 =50×2.4 =120(cm3) 故答案为:120。 【分析】根据条件“ 平行于底面截成两个长方体后,表面积比原来增加了100cm2 ”可知,增加了两个底面积,用增加的表面积÷2=长方体的底面积,然后用长方体的底面积×高=长方体的体积,据此列式解答。
四、解答题
14.【答案】 (1)解:10×6×3.5=210(平方米)
答:这间教室的空间有210平方米。
(2)解:(10×1.2+6×1.2)×2-6=38.4-6=32.4(平方米)
答:这间教室贴瓷砖的面积是32.4平方米。
【解析】【分析】(1)求这间教室的空间有多大就是求教室的体积;教室的体积=教室的长×宽×高; (2)(教室的长×瓷砖的高+教室的宽×瓷砖的高)×2=教室四周一圈四个面的面积;教室四周一圈四个面的面积- 门、窗、黑板面积=贴瓷砖的面积。
15.【答案】 (1)解:5×5+5×8×4=185(平方分米)
答:做这个水槽至少需要185平方分米铁皮。
(2)解:50÷(5×5)=2(分米)
答:水深2分米。
【解析】【分析】(1)因为这是一个无盖的水箱,所以制作时少去1个“长×卷”这个面,而且这个长方体水槽有两个面那么需要铁皮的平方分米数=长×宽+长×高×4; (2)水的深度=注入水的深度÷底面积,其中底面积=长×宽。
五、综合题
16.【答案】 (1)750 (2)1350
【解析】【解答】(1)(15×10+15×9+10×9)×2 =(150+135+90)×2 =375×2 =750(平方厘米) (2)15×10×9 =150×9 =1350(立方厘米) 故答案为:(1)750;(2)1350。
【分析】由同一个顶点引出的三条边分别为长方体的长、宽、高。根据长方体的展开图可知,长方体的长、宽、高分别为:15厘米、10厘米=9厘米。 (1)长方体的表面积=(长×宽+长×高+宽×高)×2; (2)长方体的体积=长×宽×高。
六、应用题
17.【答案】 解:(9×1.1+7.2×1.1)×2=35.64(平方米),35.64×5=178.2(元)
【解析】【解答】(9×1.1+7.2×1.1)×2 =(9.9+7.92)×2 =17.82×2 =35.64(平方米) 35.64×5=178.2(元). 答:这间教室粉刷墙围的面积是35.64平方米,粉刷这间教室需要178.2元.
【分析】根据题意可知,要求粉刷的墙围面积,用(粉刷的长度×高度+粉刷的宽度×高度)×2=粉刷的四面墙围的面积; 然后用每平方米的粉刷费用×粉刷的面积=粉刷这间教室的总费用,据此列式解答.
