2.3 平面向量的基本定理及坐标表示(共29张PPT)
文档属性
| 名称 | 2.3 平面向量的基本定理及坐标表示(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
当 时,
与 同向,
且 是 的 倍;
当 时,
与 反向,
且 是 的 倍;
当 时,
,且 。
1.复习:
⑴向量共线定理
非零向量
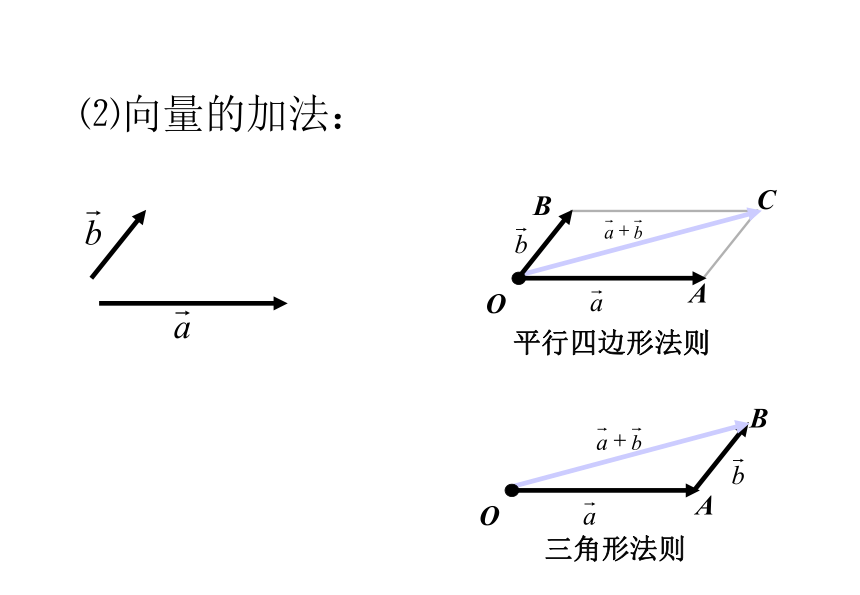
⑵向量的加法:
O
B
C
A
O
A
B
平行四边形法则
三角形法则
O
C
A
B
M
N
O
C
A
B
M
N
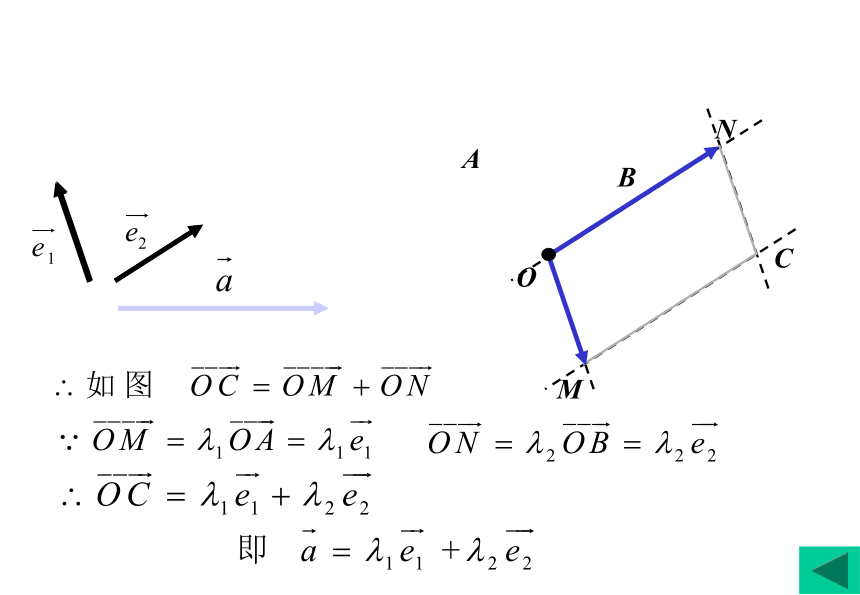
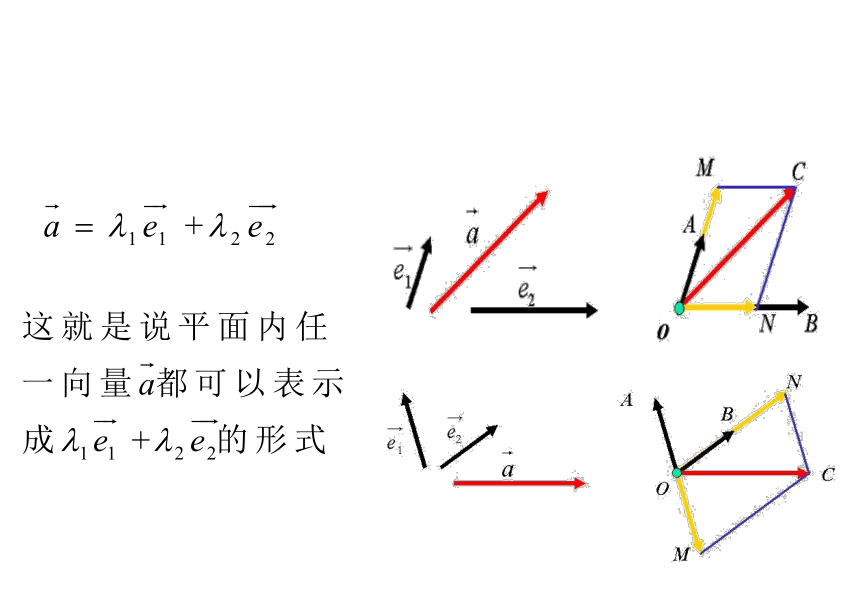
平面向量基本定理:
O
A
B
C
B
A
C
D
M
练习:
B
A
C
D
D
小结:
建议:
预复习课本P 105~108
B
O
P
A
§2.3.2 平面向量的正交分解及坐标表示
目标导学
1、掌握平面向量的坐标表示,会进行平面向量的正交分解。
2、会对平面向量进行坐标运算;会求两个向量的和与差,会对向量与数量的积进行坐标运算。
把一个向量分解为两个互相垂直的向量,叫作把向量正交分解
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
平面向量的坐标表示
①
O
x
y
A
起点在坐标原点的向量的坐标就是它的终点的坐标。
A
A1
A2
解:如图可知
同理
平面向量的坐标运算:
两个向量和(差)的坐标分别等于这两个向量相应坐标
的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的坐标
x
y
O
B
A
解:
一个向量的坐标等于表示此向量的有向线段
的终点的坐标减去起点的坐标。
解法1:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
解法2:由平行四边形法则可得
而
所以顶点D的坐标为(2,2)
§2.3.4 平面向量共线的坐标表示
目标导学
1、掌握共线向量的坐标表示;
2、会运用共线向量的坐标表示解决一些简单问题:如 证明共线、求坐标,等等。
注:1、 消去时不能两式相除,因为有可能为0;
2、 不能写成
因为x1、x2有可能为0;
3、
则当且仅当 时, 。
例2.已知 A(-1,-1),B(1,3),C(2,5),试判断A、B、C三点
之间的位置关系。
x
y
O
P1
P2
P
(1)
M
解:(1)
当 时,
与 同向,
且 是 的 倍;
当 时,
与 反向,
且 是 的 倍;
当 时,
,且 。
1.复习:
⑴向量共线定理
非零向量
⑵向量的加法:
O
B
C
A
O
A
B
平行四边形法则
三角形法则
O
C
A
B
M
N
O
C
A
B
M
N
平面向量基本定理:
O
A
B
C
B
A
C
D
M
练习:
B
A
C
D
D
小结:
建议:
预复习课本P 105~108
B
O
P
A
§2.3.2 平面向量的正交分解及坐标表示
目标导学
1、掌握平面向量的坐标表示,会进行平面向量的正交分解。
2、会对平面向量进行坐标运算;会求两个向量的和与差,会对向量与数量的积进行坐标运算。
把一个向量分解为两个互相垂直的向量,叫作把向量正交分解
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
平面向量的坐标表示
①
O
x
y
A
起点在坐标原点的向量的坐标就是它的终点的坐标。
A
A1
A2
解:如图可知
同理
平面向量的坐标运算:
两个向量和(差)的坐标分别等于这两个向量相应坐标
的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的坐标
x
y
O
B
A
解:
一个向量的坐标等于表示此向量的有向线段
的终点的坐标减去起点的坐标。
解法1:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
解法2:由平行四边形法则可得
而
所以顶点D的坐标为(2,2)
§2.3.4 平面向量共线的坐标表示
目标导学
1、掌握共线向量的坐标表示;
2、会运用共线向量的坐标表示解决一些简单问题:如 证明共线、求坐标,等等。
注:1、 消去时不能两式相除,因为有可能为0;
2、 不能写成
因为x1、x2有可能为0;
3、
则当且仅当 时, 。
例2.已知 A(-1,-1),B(1,3),C(2,5),试判断A、B、C三点
之间的位置关系。
x
y
O
P1
P2
P
(1)
M
解:(1)
