青岛版数学七下14.2 平面直角坐标系课件(60张)
文档属性
| 名称 | 青岛版数学七下14.2 平面直角坐标系课件(60张) |

|
|
| 格式 | zip | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览











文档简介
(共60张PPT)
平面直角坐标系
平面直角坐标系
如图,点A到x轴的距离为 ,到y轴的距离为 ;
点B到x轴的距离为 ,到y轴的距离为 ;
点C到x轴的距离为 ,到y轴的距离为 ;
点D到x轴的距离为 ,到y轴的距离为 ;
平面直角坐标系
讲解
3
2
2
1
1
2
2
3
笔记
P(x,y)到x轴的距离为 ;到y轴的距离为 ,x轴上的点坐标 ,y轴上的点坐标 ,
一三象限角平分线上的点坐标 ,
二四象限角平分线上的点坐标 .
|y|
平面直角坐标系
|x|
(x,0)
(0,y)
(x,x)
(x,-x)
平面直角坐标系
【示例1】
课间操时,小华、小军、小刚的位置如图,小华对小刚说“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )?
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
分析:
根据题目“小华对小刚说”这个信息,可知“我”是 ,“你”是 ,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么题中图所示就是以 为原点的平面直角坐标系的第一象限,所以小刚的位置为 .
小华
小刚
平面直角坐标系
小华
(4,3)
【示例1】
【示例2】
如果点M(a+3,a+1)在直角坐标系的x轴上,那么点M的坐标为 .
在x轴上的点, 坐标为0,
所以,a+1= ,则a= ,
从而可求出M的坐标为 .
(2,0)
纵
0
平面直角坐标系
-1
(2,0)
总结
思路点拨
x轴上的点,纵坐标为0;
y轴上的点横坐标为0;
原点的横纵坐标都为0.
如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为(4,1),表示“人民大会堂”的点的坐标为(0.-1),则表示“天安门”的点的坐标为( )
A.(0,0) B.(-1,0)
C.(1,0) D.(1,1)
答 案
C
例1
解 析
如图所示:“天安门的点的坐标为:(1,0).故选:C.
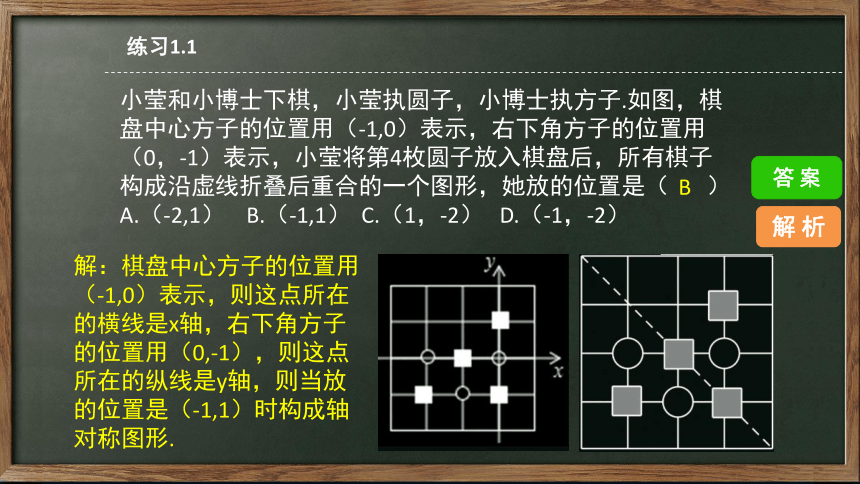
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,小莹将第4枚圆子放入棋盘后,所有棋子构成沿虚线折叠后重合的一个图形,她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
B
练习1.1
解:棋盘中心方子的位置用(-1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,-1),则这点所在的纵线是y轴,则当放的位置是(-1,1)时构成轴对称图形.
答 案
解 析
答 案
例2
B
点A(m-3,m-1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(-2,0) C.(2,0) D.(0,2)
答 案
练习2.1
解 析
如果点(m+5,2-4m)在x轴上,那么m的值等于 .
根据题意,得:2-4m=0,
解得:m= ,
故答案为:
答 案
5; 3
例3
解 析
点(-3,5)到x轴的距离是 ,到y轴的距离是 .
∵点的坐标为(-3,5),
∴点到x轴的距离等于其纵坐标5的绝对值,即为5;点到y轴的距离等于其横坐标-3的绝对值,即为3.所以答案分别为5,3
答 案
练习3.1
C
点P(-5,-6)到x轴的距离是( )
A.5 B.-5 C.6 D.-6
答 案
例4
解 析
若点P在x轴的下方,y轴的左方,到每条坐标轴的距离都是3,则坐标为( )
A.(3,3) B.(3,-3) C.(-3,-3) D.(-3,3)
C
解:∵点P在x轴下方,y轴的左方,
∴点P是第三象限内的点,
∵第三象限内的点的特点是(-,-),且点到各坐标轴的距离都是3,
∴点P的坐标轴为(-3,-3).
已知点P位于y轴的右侧且位于x轴下方,到x轴、y轴距离分别是4个单位长度、3个单位长度,则点P的坐标( )
A.(3,-4) B.(-3,4) C.(4,-3) D.(-4,3)
答 案
练习4.1
解 析
A
∵点P位于y轴的右侧且位于x轴下方,到x轴、y轴距离分别是4个单位、3个单位,
∴点P的纵坐标为-4,点P的横坐标为3,
∴点P的坐标为(3,-4).
坐标系中的面积计算
坐标系中的面积计算
答 案
讲解
(1)坐标系中的面积计算
如图:△OAB的面积为
OB
AC
7
4
17
坐标系中的面积计算
答 案
讲解
(1)坐标系中的面积计算
如图:△ABC的面积为
S△BCP
3 2
3 1
3 3
9
S△ABP
割:
坐标系中的面积计算
答 案
讲解
如图:求△ABC的面积.
补:
答 案
规则图形:一条平行于坐标轴,可直接用 求解.
不规则图形可以用割补法,转化为规则图形.
割:把所有图形切割成几个规则图形,每个图形分别求面积,然后再求各个图形的 ;
补:把所求图形补全成一个 ,再用全部图形的面积剪去多余图形的面积.
笔记
坐标系中的面积计算
公式法
面积和
长方形 或者梯形
答 案
15
例5
解 析
(1)已知:A(-4,-5),B(-2,0),C(4,0),求△ABC的面积.
(1).在平面直角坐标系中,△ABC的各个顶点坐标分别为A(-4,-2),B(4,-2),C(2,-2),则△ABC的面积为( ).
A.8 B.16 C.32 D.64
答 案
B
练习5.1
答 案
10
例5
(2).如图,小方格的边长为1,△ABC的顶点都在格点上,请在方格纸上建立平面直角坐标系,并计算△ABC的面积.
例5
解 析
(2).如图,小方格的边长为1,△ABC的顶点都在格点上,请在方格纸上建立平面直角坐标系,并计算△ABC的面积.
如图建立坐标系,则A(0,2),B(4,0),C(2,6),如图作矩形BEDO,
S△ABC=S四边形BEDO-S△AOB-S△DCA-S△BCE
=24-4-4-6=10
答 案
例5
解 析
(3)在平面直角坐标系中,点A(0,-1),点B(0,-4),已知点C在x轴上,若△ABC的面积是9,求点C的坐标.
(±6,0)
(2).如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中A点坐标为(2,-1),则△ABC的面积为( )
A.3 B.4 C.5 D.6
答 案
C
练习5.1
坐标系中的平移与对称
引入
坐标系中的平移与对称
【示例1】分析下图,回答问题:
如图,线段A?B?是由线段AB平移得到的,点A(-2,3)变为A?(3,4), 那么,B?点的坐标是 .
A先向右平移5个单位,再向上平移一个单位;
B先向右平移5个单位,再向上平移一个单位
答 案
(2,2)
坐标系中的平移与对称
思路点拨
坐标系中的平移与对称
总结
左右平移:左减右加纵不变
上下平移:上加下减横不变
线和图形的平移:当做一个主体,每个点的坐标的变化都遵从同样的规律
总结
左右平移:左减右加纵不变
上下平移:上加下减横不变
线和图形的平移:当做一个主体,每个点的坐标的变化都遵从同样的规律
【示例2】分析下图,回答问题:
(1)如图,将点A(1,2)关于x轴对称得到点A?,A?的坐标为 .
将点B(3,1)关于x轴对称得到点B?,B?的坐标为 .
那么,线段A?B?与线段AB关于 轴对称.
答 案
(1,-2)
坐标系中的平移与对称
(3,-1)
x
【示例2】分析下图,回答问题:
(2)如图,将点A?(1,-2)关于y轴对称得到点A?,A?的坐标为 .
将点B?(3,-1)关于y轴对称得到点B?,B?的坐标为 .
那么,线段A?B?与线段A?B?关
于 轴对称.
答 案
坐标系中的平移与对称
(-1,-2)
(-3,-1)
y
【示例2】分析下图,回答问题:
(3)如图,将点A(1,2)关于原点对称得到点A?,A?的坐标为 .
将点B(3,1)关于原点对称得到点B?,B?的坐标为 .
那么,线段AB与线段A?B?关
于 轴对称.
答 案
坐标系中的平移与对称
(-1,-2)
(-3,-1)
原点
总结
点关于x轴对称,横不变,纵相反;
点关于y轴对称,纵不变,横相反;
点关于原点对称,横纵都相反.
坐标系中的平移与对称
(1)已知点M(3,-2),将它先向左平移4个单位长度,再向上平移3个单位长度后得到点N,则点N的坐标为 .将点P向下平移5个单位长度,再向左平移1个单位长度后的坐标为(-2,-3),则点P的坐标是 .
(2)已知点A的坐标为(3,-2),现保持点A不动,将平面直角坐标系向左平移3个单位长度,向上平移4个单位长度,平移后点A的坐标为 .
(-1,1)
例6
(-1,2)
(6,-6)
(1,2)
例6
(3)线段CD是由线段AB平移得到的,若点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 .
(4)点A、B的坐标分别为(1,0)、(0,2),若将线段AB平移至A1B1,且点A1、B1的坐标分别为(2,0)、(b,3),则a+b= .
2
例6
例6
(5)如图,已知△ABC的各顶点坐标为A(4,6),B(5,2),C(2,1),将△ABC平移得到△A1B1C1,三角形某一边上一点P(x,y)的对应点为P‘(x+4,y-2),求出△A1B1C1各个顶点的坐标,并画出△A1B1C1.
答 案
例6
由平移知A1(8,4)B1(9,0)C1(6,-1),在平面直角坐标系中顺次连接各点即可.
答 案
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2)
(1).写出A、B的坐标A 、
B .
(2,1)
(4,3)
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2)
(2).将△ABC向左平移1个单位长度,
再向上平移2个单位长度,得到△A’B‘C’,
则△A’B‘C’的三个顶点坐标分别是
A’ ;
B‘ ;
C’ .
答 案
练习6.1
(1,1)
(3,5)
(0,4)
答 案
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中C点的坐标为(1,2)
(3)△ABC的面积为 平
方单位.
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2). (4)画出平移后的三角形.
答 案
(2,-3)
(-2,3)
(-2,-3)
y轴
例7
(1)点A(2,3)关于x轴的对称点A1的坐标为 ;点A关于y轴的对称点A2的坐标为 ;点A关于原点的对称点A3的坐标为 ;点A3与点A1关于 对称.
答 案
1
例7
-2
(2)已知点P(a+3b,3)与点Q(-5,a+2b)关于x轴对称,则a= ,b= .
答 案
例7
(3).如图,在平面直角坐标系中,△ABC的顶点坐标为A
(-1,-1),B(2,1),C(0,2).若△ABC与△A?B?C?关于原点对
称,△ABC与△A?B?C?关于y轴对称,
作出△A?B?C?和△A?B?C?,
并说明△A?B?C?和△A?B?C?关于
哪条直线对称.
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(1)在图中作出△ABC关于x轴的对称图形△A1B1C1.
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(2)写出A1、B1、C1的坐标(直接写答案)
由图可知,A1(1,-2),B1(3,-1),C1(-2,1)
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(3)求△ABC的面积.
坐标系中的规律问题
如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),···,那么点A2019的坐标为( )?
A.(1008,1)
B.(1009,1)
C.(1009,0)
D.(1010,0)
坐标系中的规律问题
【示例1】
解:根据题意和图的坐标可知:每次移动一个单位按向上、向右、向下、向右的方向依次不断地移动,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)、A5(2,1)、A6 、A7(3,0),···
坐标变化的规律:每移动4次,它的纵坐标都为0,而横坐标向右移动了2个单位长度,也就是移动次数的一半.
坐标系中的规律问题
【分析解答】
(3,1)
∴A2019纵坐标是 的纵坐标 .
∴A019横坐标是0+2×504+ =1009.
那么点A2019的坐标为 ,
故选 .
坐标系中的规律问题
【分析解答】
504
1
3
A?
0
(1009,0)
C
坐标系中的规律问题
【示例2】如图,在平面直角坐标系上有A(1,0)点,点A第一次跳动至点A1(-1,1),第二次向右跳动3个单位长度至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位长度至点A4(3,2),···,依此规律跳动下去,点A第2018次跳动至点A2018的坐标是 ?
坐标系中的规律问题
故第2018次跳动至点的坐标是 .
(1010,1009)
总结
坐标系内的规律问题大致分为下列两种:
(1)递进规律:坐标系内的点按照一定的规律排列;
(2)周期规律:坐标系内的一列点,周期性出现.
坐标系中的规律问题
解:观察发现,
第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是 ,
第8次跳动至点的坐标是 ,
······
第2n次跳动至点的坐标是 ,
(4,3)
(5,4)
(n+1,n)
答 案
例8
在平面直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).电子蛙从P1(1,1)出发,依次以A、B、O为对称中心跳跃,即第一步跳动P1关于A的对称点P2,第二步跳到P2关于B的对称点P3,第三步跳到P3关于O的对称点P4,以此类推.试写出P2、P7、P100的坐标.
在如图所示的平面直角坐标系中,一只蚂蚁从点A出发,沿着A—B—C—D—A循环爬行,其中A点的坐标为(1,-1),B点的坐标为(-1,-1),C点的坐标为(-1,3),D点的坐标为(1,3),当蚂蚁爬了2017个单位长度时,它所处的位置的坐标为( )
A.(1,0) B.(0,-1)
C.(-1,-1) D.(-1,0)
答 案
B
练习8.1
Thank you
平面直角坐标系
平面直角坐标系
如图,点A到x轴的距离为 ,到y轴的距离为 ;
点B到x轴的距离为 ,到y轴的距离为 ;
点C到x轴的距离为 ,到y轴的距离为 ;
点D到x轴的距离为 ,到y轴的距离为 ;
平面直角坐标系
讲解
3
2
2
1
1
2
2
3
笔记
P(x,y)到x轴的距离为 ;到y轴的距离为 ,x轴上的点坐标 ,y轴上的点坐标 ,
一三象限角平分线上的点坐标 ,
二四象限角平分线上的点坐标 .
|y|
平面直角坐标系
|x|
(x,0)
(0,y)
(x,x)
(x,-x)
平面直角坐标系
【示例1】
课间操时,小华、小军、小刚的位置如图,小华对小刚说“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )?
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
分析:
根据题目“小华对小刚说”这个信息,可知“我”是 ,“你”是 ,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么题中图所示就是以 为原点的平面直角坐标系的第一象限,所以小刚的位置为 .
小华
小刚
平面直角坐标系
小华
(4,3)
【示例1】
【示例2】
如果点M(a+3,a+1)在直角坐标系的x轴上,那么点M的坐标为 .
在x轴上的点, 坐标为0,
所以,a+1= ,则a= ,
从而可求出M的坐标为 .
(2,0)
纵
0
平面直角坐标系
-1
(2,0)
总结
思路点拨
x轴上的点,纵坐标为0;
y轴上的点横坐标为0;
原点的横纵坐标都为0.
如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为(4,1),表示“人民大会堂”的点的坐标为(0.-1),则表示“天安门”的点的坐标为( )
A.(0,0) B.(-1,0)
C.(1,0) D.(1,1)
答 案
C
例1
解 析
如图所示:“天安门的点的坐标为:(1,0).故选:C.
小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,小莹将第4枚圆子放入棋盘后,所有棋子构成沿虚线折叠后重合的一个图形,她放的位置是( )
A.(-2,1) B.(-1,1) C.(1,-2) D.(-1,-2)
B
练习1.1
解:棋盘中心方子的位置用(-1,0)表示,则这点所在的横线是x轴,右下角方子的位置用(0,-1),则这点所在的纵线是y轴,则当放的位置是(-1,1)时构成轴对称图形.
答 案
解 析
答 案
例2
B
点A(m-3,m-1)在x轴上,则A点的坐标为( )
A.(0,-2) B.(-2,0) C.(2,0) D.(0,2)
答 案
练习2.1
解 析
如果点(m+5,2-4m)在x轴上,那么m的值等于 .
根据题意,得:2-4m=0,
解得:m= ,
故答案为:
答 案
5; 3
例3
解 析
点(-3,5)到x轴的距离是 ,到y轴的距离是 .
∵点的坐标为(-3,5),
∴点到x轴的距离等于其纵坐标5的绝对值,即为5;点到y轴的距离等于其横坐标-3的绝对值,即为3.所以答案分别为5,3
答 案
练习3.1
C
点P(-5,-6)到x轴的距离是( )
A.5 B.-5 C.6 D.-6
答 案
例4
解 析
若点P在x轴的下方,y轴的左方,到每条坐标轴的距离都是3,则坐标为( )
A.(3,3) B.(3,-3) C.(-3,-3) D.(-3,3)
C
解:∵点P在x轴下方,y轴的左方,
∴点P是第三象限内的点,
∵第三象限内的点的特点是(-,-),且点到各坐标轴的距离都是3,
∴点P的坐标轴为(-3,-3).
已知点P位于y轴的右侧且位于x轴下方,到x轴、y轴距离分别是4个单位长度、3个单位长度,则点P的坐标( )
A.(3,-4) B.(-3,4) C.(4,-3) D.(-4,3)
答 案
练习4.1
解 析
A
∵点P位于y轴的右侧且位于x轴下方,到x轴、y轴距离分别是4个单位、3个单位,
∴点P的纵坐标为-4,点P的横坐标为3,
∴点P的坐标为(3,-4).
坐标系中的面积计算
坐标系中的面积计算
答 案
讲解
(1)坐标系中的面积计算
如图:△OAB的面积为
OB
AC
7
4
17
坐标系中的面积计算
答 案
讲解
(1)坐标系中的面积计算
如图:△ABC的面积为
S△BCP
3 2
3 1
3 3
9
S△ABP
割:
坐标系中的面积计算
答 案
讲解
如图:求△ABC的面积.
补:
答 案
规则图形:一条平行于坐标轴,可直接用 求解.
不规则图形可以用割补法,转化为规则图形.
割:把所有图形切割成几个规则图形,每个图形分别求面积,然后再求各个图形的 ;
补:把所求图形补全成一个 ,再用全部图形的面积剪去多余图形的面积.
笔记
坐标系中的面积计算
公式法
面积和
长方形 或者梯形
答 案
15
例5
解 析
(1)已知:A(-4,-5),B(-2,0),C(4,0),求△ABC的面积.
(1).在平面直角坐标系中,△ABC的各个顶点坐标分别为A(-4,-2),B(4,-2),C(2,-2),则△ABC的面积为( ).
A.8 B.16 C.32 D.64
答 案
B
练习5.1
答 案
10
例5
(2).如图,小方格的边长为1,△ABC的顶点都在格点上,请在方格纸上建立平面直角坐标系,并计算△ABC的面积.
例5
解 析
(2).如图,小方格的边长为1,△ABC的顶点都在格点上,请在方格纸上建立平面直角坐标系,并计算△ABC的面积.
如图建立坐标系,则A(0,2),B(4,0),C(2,6),如图作矩形BEDO,
S△ABC=S四边形BEDO-S△AOB-S△DCA-S△BCE
=24-4-4-6=10
答 案
例5
解 析
(3)在平面直角坐标系中,点A(0,-1),点B(0,-4),已知点C在x轴上,若△ABC的面积是9,求点C的坐标.
(±6,0)
(2).如图,在平面直角坐标系中,△ABC的顶点都在网格点上,其中A点坐标为(2,-1),则△ABC的面积为( )
A.3 B.4 C.5 D.6
答 案
C
练习5.1
坐标系中的平移与对称
引入
坐标系中的平移与对称
【示例1】分析下图,回答问题:
如图,线段A?B?是由线段AB平移得到的,点A(-2,3)变为A?(3,4), 那么,B?点的坐标是 .
A先向右平移5个单位,再向上平移一个单位;
B先向右平移5个单位,再向上平移一个单位
答 案
(2,2)
坐标系中的平移与对称
思路点拨
坐标系中的平移与对称
总结
左右平移:左减右加纵不变
上下平移:上加下减横不变
线和图形的平移:当做一个主体,每个点的坐标的变化都遵从同样的规律
总结
左右平移:左减右加纵不变
上下平移:上加下减横不变
线和图形的平移:当做一个主体,每个点的坐标的变化都遵从同样的规律
【示例2】分析下图,回答问题:
(1)如图,将点A(1,2)关于x轴对称得到点A?,A?的坐标为 .
将点B(3,1)关于x轴对称得到点B?,B?的坐标为 .
那么,线段A?B?与线段AB关于 轴对称.
答 案
(1,-2)
坐标系中的平移与对称
(3,-1)
x
【示例2】分析下图,回答问题:
(2)如图,将点A?(1,-2)关于y轴对称得到点A?,A?的坐标为 .
将点B?(3,-1)关于y轴对称得到点B?,B?的坐标为 .
那么,线段A?B?与线段A?B?关
于 轴对称.
答 案
坐标系中的平移与对称
(-1,-2)
(-3,-1)
y
【示例2】分析下图,回答问题:
(3)如图,将点A(1,2)关于原点对称得到点A?,A?的坐标为 .
将点B(3,1)关于原点对称得到点B?,B?的坐标为 .
那么,线段AB与线段A?B?关
于 轴对称.
答 案
坐标系中的平移与对称
(-1,-2)
(-3,-1)
原点
总结
点关于x轴对称,横不变,纵相反;
点关于y轴对称,纵不变,横相反;
点关于原点对称,横纵都相反.
坐标系中的平移与对称
(1)已知点M(3,-2),将它先向左平移4个单位长度,再向上平移3个单位长度后得到点N,则点N的坐标为 .将点P向下平移5个单位长度,再向左平移1个单位长度后的坐标为(-2,-3),则点P的坐标是 .
(2)已知点A的坐标为(3,-2),现保持点A不动,将平面直角坐标系向左平移3个单位长度,向上平移4个单位长度,平移后点A的坐标为 .
(-1,1)
例6
(-1,2)
(6,-6)
(1,2)
例6
(3)线段CD是由线段AB平移得到的,若点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标为 .
(4)点A、B的坐标分别为(1,0)、(0,2),若将线段AB平移至A1B1,且点A1、B1的坐标分别为(2,0)、(b,3),则a+b= .
2
例6
例6
(5)如图,已知△ABC的各顶点坐标为A(4,6),B(5,2),C(2,1),将△ABC平移得到△A1B1C1,三角形某一边上一点P(x,y)的对应点为P‘(x+4,y-2),求出△A1B1C1各个顶点的坐标,并画出△A1B1C1.
答 案
例6
由平移知A1(8,4)B1(9,0)C1(6,-1),在平面直角坐标系中顺次连接各点即可.
答 案
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2)
(1).写出A、B的坐标A 、
B .
(2,1)
(4,3)
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2)
(2).将△ABC向左平移1个单位长度,
再向上平移2个单位长度,得到△A’B‘C’,
则△A’B‘C’的三个顶点坐标分别是
A’ ;
B‘ ;
C’ .
答 案
练习6.1
(1,1)
(3,5)
(0,4)
答 案
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中C点的坐标为(1,2)
(3)△ABC的面积为 平
方单位.
练习6.1
如图,在直角坐标系中,△ABC的顶点都在网格点上,其中c点的坐标为(1,2). (4)画出平移后的三角形.
答 案
(2,-3)
(-2,3)
(-2,-3)
y轴
例7
(1)点A(2,3)关于x轴的对称点A1的坐标为 ;点A关于y轴的对称点A2的坐标为 ;点A关于原点的对称点A3的坐标为 ;点A3与点A1关于 对称.
答 案
1
例7
-2
(2)已知点P(a+3b,3)与点Q(-5,a+2b)关于x轴对称,则a= ,b= .
答 案
例7
(3).如图,在平面直角坐标系中,△ABC的顶点坐标为A
(-1,-1),B(2,1),C(0,2).若△ABC与△A?B?C?关于原点对
称,△ABC与△A?B?C?关于y轴对称,
作出△A?B?C?和△A?B?C?,
并说明△A?B?C?和△A?B?C?关于
哪条直线对称.
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(1)在图中作出△ABC关于x轴的对称图形△A1B1C1.
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(2)写出A1、B1、C1的坐标(直接写答案)
由图可知,A1(1,-2),B1(3,-1),C1(-2,1)
答 案
练习7.1
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).(3)求△ABC的面积.
坐标系中的规律问题
如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0),···,那么点A2019的坐标为( )?
A.(1008,1)
B.(1009,1)
C.(1009,0)
D.(1010,0)
坐标系中的规律问题
【示例1】
解:根据题意和图的坐标可知:每次移动一个单位按向上、向右、向下、向右的方向依次不断地移动,得到点A1(0,1)、A2(1,1)、A3(1,0)、A4(2,0)、A5(2,1)、A6 、A7(3,0),···
坐标变化的规律:每移动4次,它的纵坐标都为0,而横坐标向右移动了2个单位长度,也就是移动次数的一半.
坐标系中的规律问题
【分析解答】
(3,1)
∴A2019纵坐标是 的纵坐标 .
∴A019横坐标是0+2×504+ =1009.
那么点A2019的坐标为 ,
故选 .
坐标系中的规律问题
【分析解答】
504
1
3
A?
0
(1009,0)
C
坐标系中的规律问题
【示例2】如图,在平面直角坐标系上有A(1,0)点,点A第一次跳动至点A1(-1,1),第二次向右跳动3个单位长度至点A2(2,1),第三次跳动至点A3(-2,2),第四次向右跳动5个单位长度至点A4(3,2),···,依此规律跳动下去,点A第2018次跳动至点A2018的坐标是 ?
坐标系中的规律问题
故第2018次跳动至点的坐标是 .
(1010,1009)
总结
坐标系内的规律问题大致分为下列两种:
(1)递进规律:坐标系内的点按照一定的规律排列;
(2)周期规律:坐标系内的一列点,周期性出现.
坐标系中的规律问题
解:观察发现,
第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是 ,
第8次跳动至点的坐标是 ,
······
第2n次跳动至点的坐标是 ,
(4,3)
(5,4)
(n+1,n)
答 案
例8
在平面直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0).电子蛙从P1(1,1)出发,依次以A、B、O为对称中心跳跃,即第一步跳动P1关于A的对称点P2,第二步跳到P2关于B的对称点P3,第三步跳到P3关于O的对称点P4,以此类推.试写出P2、P7、P100的坐标.
在如图所示的平面直角坐标系中,一只蚂蚁从点A出发,沿着A—B—C—D—A循环爬行,其中A点的坐标为(1,-1),B点的坐标为(-1,-1),C点的坐标为(-1,3),D点的坐标为(1,3),当蚂蚁爬了2017个单位长度时,它所处的位置的坐标为( )
A.(1,0) B.(0,-1)
C.(-1,-1) D.(-1,0)
答 案
B
练习8.1
Thank you
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
