青岛版数学八下11.1 图形的平移课件(57张)
文档属性
| 名称 | 青岛版数学八下11.1 图形的平移课件(57张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 19:15:47 | ||
图片预览











文档简介
(共57张PPT)
图形的平移与旋转
图形的平移
平移的概念
物体在传送带上又是如何运动的呢?
引入
平移的概念
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为 .
讲 解
平移不改变图形的 和 .
笔 记
平移
形状
大小
平移的概念
平移只能沿某一方向运动,且前后全等
总结
【示例1】下列图形中,不能通过其中一个四边形平移得到的是( )
A. B.
C. D.
答 案
D
例1
如图,不是平移设计的是( )
A. B. C. D.
D
解析
D选项可以利用旋转变换得到,无法利用平移得到.
故选:D.
练习1.1
下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
C
解析
A、利用图形旋转而成;B、利用轴对称而成;D、利用图形旋转而成;只有C选项是图形平移而成,故选C
平移的概念
平移前后图形全等,且平移距离为对应点移动距离
总结
【示例1】如图,将△ABC沿射线BC方向平移至△DEF.
(1)点A平移至点 ,线段 平移至线段EF;
(2)若平移距离为3,则AD= ;
(3)若BE=2,则平移距离为 .
答 案
D
BC
3
2
例2
答 案
将线段AB向右平移3cm得到线段CD,如果AB=5cm,则
CD=( )
A.3cm B.8cm C.2cm D.5cm
D
练习2.1
答 案
如图,△ABC沿BC平移得到△DCE,下列说法正确的是( )
A.点B的对应点是点E B.点C的对应点是点E
C.点C的对应点是点C D.点C没有移动位置
B
练习2.2
答 案
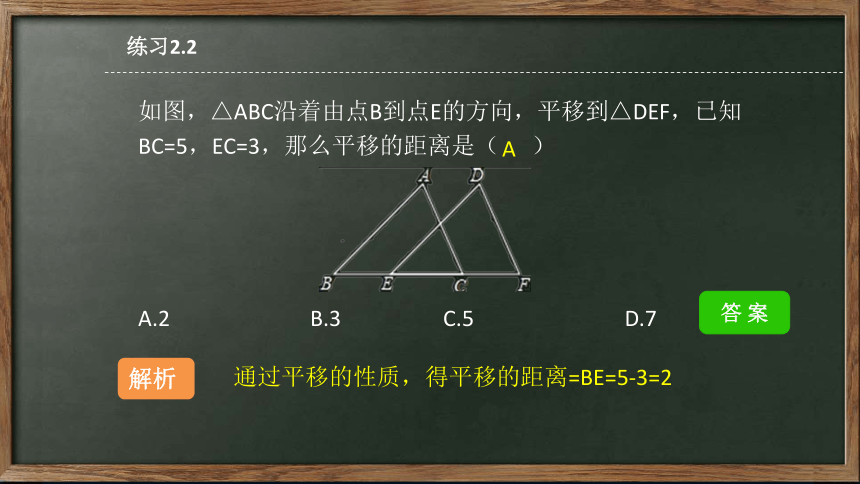
如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离是( )
A.2 B.3 C.5 D.7
A
解析
通过平移的性质,得平移的距离=BE=5-3=2
平移的性质
派大星和海绵宝宝学会了瞬间移动,从后往前平移过程中,你能找到哪些线段平行且相等吗?
引入
一个图形和他经过平移所得的图形中,对应点所连的线段 (或在同一条直线上)且 ;对应线段 (或在同一条直线上)且 ,对应角 .
平移的性质
答 案
平移前后图形全等,线段AB平移后为线段 ,则AB平行且等于 .平移前后,点A的对应点为点 ,点B的对应点为点 ,点C的对应点为 ,则AA'平行且等于
或 .
A'B'
A'
C'
B'
讲 解
笔 记
A'B'
BB'
CC'
平行
平行
相等
相等
相等
平移的性质
【示例1】如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A. 8 B.10
C. 12 D.14
答 案
C
分析:平移前后,图形全等,则△ABC≌ ,所以AC= ,BC= ,根据平移的性质,可以得到AD= = ,四边形ABFD的周长为AB+BF+DF+AD=AB+BC+ +DF+AD,而AB+BF+
DF恰为 的周长,因△ABC平移1个单位得到△DEF,则AD=CF= ,所以四边形ABFD的周长为 .
△DEF
DF
EF
BE
CF
CF
△ABC
1
10+1+1=12
平移的对应元素:
对应点、对应角、对应线段
总 结
平移的性质
例3
答 案
如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A. 16cm B. 18cm
C. 20cm D. 22cm
C
解 析
例3
根据题意,将周长为16cm的△ABC沿BC向右平移2cm得到△DEF,
∴AD=CF=2cm,BF=BC+CF=BC=2cm,DF=AC;
又∵AB+BC+AC=16cm,
∴四边形ABFD的周长
=AD+AB+BF+DF=2+AB+BC+2+AC
=20cm
解 析
练习3.1
答 案
将线段AB平移1cm,得到线段A'B',则点A到点A'的距离
是 cm.
1
解 析
在平移的过程中各点的运动状态是一样的,现在将线段平移1cm,则每一点都平移1cm,
即AA'=1cm,
∴点A到点A'的距离是1cm.
练习3.2
答 案
如图,已知线段AB的长度为2cm,将线段AB向下平移2.5cm后得到线段A'B',连接AA',BB',则四边形AA'B'B的周长为( )
A. 4.5cm
B. 8cm
C. 9cm
D. 10cm
C
练习3.3
答 案
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )
A. 12 B. 24
C. 48 D. 60
B
解 析
练习3.3
由平移的性质可知,FE=BC=8,四边形ABED为平行四边形,
∵F为BC的中点,
∴BF=4,
∴BE=FE=FB=4,
∴四边形ABED的面积=4×6=24
故选B
解 析
分析:△ABC向右平移2个单位,再向上平移3个单位,可以理解为点A、点B、点C分别向 平移 个单位,再向 平移
个单位后变为点A1、点B1、点C1,
确定后连接各点即为△A1B1C1的位置;
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(1)△ABC的顶点都在方格纸的格点上,
先将△ABC向右平移2个单位,再向上平移
3个单位,得到△A1B1C1,其中点A1,B1,
C1分别是A,B,C的对应点,试画出△1B1C1;
平移的性质
答 案
右
2
3
B1
A1
C1
上
思路点拨
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 ,线段AA1、BB1的数量关系为 ;
平移的性质
答 案
平行
相等
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(3)△A1B1C1的面积为 .(平方单位).
(3)若以线段A1C1的长度为 作为底,
则△A1B1C1高为 ,面积为 .
平移的性质
答 案
3
2
3
3
思路点拨
平移画图步骤:
1.找到原图形中的关键点
2.根据平移的方向和平移的距离,画出对应点
3.连接对应点,画出图形
总 结
平移的性质
例4
答 案
为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至A'的位置,使点A与A'对应,得到△A'B'C';
例5
根据网格结构找出点B、C平移后的对应点B'、C'的位置,再与点A'顺次连接即可.
答 案
解 析
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(2)线段AA'与BB'的关系是: ;
答 案
平行且相等
解 析
根据平移的性质解答;
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(3)求△ABC的面积;
答 案
解 析
利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解
△ABC的面积
图形的旋转
旋转的概念和性质
引入
观察上面图片,你能发现都在做什么动作吗?
在平面内,将一个图形绕一个一个定点按某个方向转动一个角度,图形的这种变化称为 ,这个定点称为 ,转动的角称为 .
讲 解
旋转
旋转中心
旋转角
如图,△ABC≌ ,点A旋转到了点 ,∠AOD= .
= ,BO= ,AO= ,CO= .
△DEF
D
∠BOE
∠COF
EO
FO
DO
旋转的概念和性质
旋转不改变图形的 和 .
一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离 ,任何一组对应点与旋转中心的连线所成的角都等于 ;对应线段相等,对应角相等.
笔 记
形状
大小
旋转的概念和性质
相等
旋转角
将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
答 案
旋转的概念和性质
旋转时需注意顺时针方向还是逆时针方向
注意
单步训练
B
【示例】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )
A.15° B.20°
C.25° D.30°
分析:旋转前后图形全等,所以△ABC≌ ,∠B= ,AE= ,因∠CAE=60°,所以∠ACE= ,因∠B=40°,,则∠DAC=∠ACE- =60°- = .
答 案
△ADE
∠D
旋转中的边角计算
思路点拨
AC
60°
∠D
60°
20°
B
先确定旋转中心、旋转角度、旋转方向,再根据边角关系计算.
总结
旋转中的边角计算
先确定旋转中心、旋转角度、旋转方向,再根据边角关系计算.
总结
例6
答 案
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A.70° B.80°
C.84° D.86°
B
解 析
有旋转的性质可知:∠B=∠AB1C1,AB=AB1,∠BAB1=100°.
∵AB=AB1,∠BAB1=100°
∴∠B=∠BB1A=40°
∴∠AB1C1=40°
∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°
练习6.1
答 案
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=20°,则∠B= 度.
65
解 析
∵Rt△ABC绕直角顶点C顺时针
旋转90°,得到△A'B'C',
∴∠ACA'=90°,CA=CA',∠B=∠CB'A',
∴△CAA'=45°,
∵∠CB'A'=∠B'AC+∠1=45°+20°=65°
∴∠B=65°.
【示例】已知:如图,△A'B'C'是由△ABC以点O为中心经过一次旋转得到的,点A'、B'、C'分别是点A、B、C旋转后的对应点.
求作:旋转中心O.
分析:找图形旋转中心的步骤:
1.先找到原图形和旋转后图形的两组对应点;
2.连接两组对应点,出现两条线段,分别作这两条线段的 ,则这两条 的交点就是 .
已知旋转前后图形,确定旋转中心
答 案
垂直平分线
旋转中心
思路点拨
O
垂直平分线
【示例】已知△ABC,如图,请画出以点C为旋转中心,旋转角为30°,按顺时针方向旋转后的图形△A'B'C'.(用直尺和量角器即可)
已知旋转前后图形,确定旋转中心
画旋转图形的步骤:
1.确定旋转中心、旋转方向、旋转角度
2.选取关键点,以旋转中心为圆心,沿题中的方向和角度分别作出各关键点的对应点
3.顺次连接作出的对应点,即为旋转后图形
总结
(1)在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
例7
答 案
B
(2)画出△ABC绕点 C顺时针旋转90°后的图形△A'B'C.
例7
答 案
中心对称
中心对称
引入
生活中的阴阳八卦图、剪纸等,都和旋转有着密不可分的关系,那这两个图都可由自身的一部分旋转多少度得到呢?
中心对称
答 案
讲 解
在平面内,如果把一个图形绕某个点旋转 后,能与另一个图形重合,那么就说这两个图形关于这个点成 ,这个点叫 .
在平面内,把一个图形绕某个点旋转 后,如果旋转前后的图形互相重合,那么这个图形叫做 ,这个点就是它的 .
成中心对称的两个图形中,对应点的连线经过 ,且被对称中心 .
总结
180°
中心对称
对称中心
180°
中心对称图形
对称中心
对称中心
平分
【示例】观察下列汽车标志,其中是中心对称图形的是( )
答 案
中心对称图形
图形旋转180°后不变的即为中心对称图形
注意
C
下列图案中,可以看作中心对称图形的是( )
A. B. C. D.
答 案
例8
C
在以下回收、绿色食品、节能、节水四个标志中,是中心对称图形的是( )
A. B. C. D.
答 案
练习8.1
D
【示例】如图,已知△ABC和点O,在图中画出△A'B'C',使△ABC与△A'B'C'关于O点中心对称.
答 案
中心对称图形
思路点拨
连接AO、BO、CO并延长,再截取等线段
找到对应点,连接各对应点即为中心对称后图形
【示例】如图所示的两个图形成中心对称,请找出它的对称中心
答 案
中心对称图形
两图形成中心对称,则对应点连线的交点即为对称中心
总结
总结
中心对称图形
例9
答 案
在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成
中心对称的△A1B1C1,再把向上
平移4个单位长度得到△A2B2C2
例9
答 案
如图所示
例9
答 案
在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(2)△A2B2C2与△ABC是否
关于某点成中心对称?若是,
直接写出对称中心的坐标;若不是,
请说明理由.
由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
Thank you
图形的平移与旋转
图形的平移
平移的概念
物体在传送带上又是如何运动的呢?
引入
平移的概念
在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变化称为 .
讲 解
平移不改变图形的 和 .
笔 记
平移
形状
大小
平移的概念
平移只能沿某一方向运动,且前后全等
总结
【示例1】下列图形中,不能通过其中一个四边形平移得到的是( )
A. B.
C. D.
答 案
D
例1
如图,不是平移设计的是( )
A. B. C. D.
D
解析
D选项可以利用旋转变换得到,无法利用平移得到.
故选:D.
练习1.1
下列四幅图案可以看作是以图案中某部分为基本图形平移得到的是( )
C
解析
A、利用图形旋转而成;B、利用轴对称而成;D、利用图形旋转而成;只有C选项是图形平移而成,故选C
平移的概念
平移前后图形全等,且平移距离为对应点移动距离
总结
【示例1】如图,将△ABC沿射线BC方向平移至△DEF.
(1)点A平移至点 ,线段 平移至线段EF;
(2)若平移距离为3,则AD= ;
(3)若BE=2,则平移距离为 .
答 案
D
BC
3
2
例2
答 案
将线段AB向右平移3cm得到线段CD,如果AB=5cm,则
CD=( )
A.3cm B.8cm C.2cm D.5cm
D
练习2.1
答 案
如图,△ABC沿BC平移得到△DCE,下列说法正确的是( )
A.点B的对应点是点E B.点C的对应点是点E
C.点C的对应点是点C D.点C没有移动位置
B
练习2.2
答 案
如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离是( )
A.2 B.3 C.5 D.7
A
解析
通过平移的性质,得平移的距离=BE=5-3=2
平移的性质
派大星和海绵宝宝学会了瞬间移动,从后往前平移过程中,你能找到哪些线段平行且相等吗?
引入
一个图形和他经过平移所得的图形中,对应点所连的线段 (或在同一条直线上)且 ;对应线段 (或在同一条直线上)且 ,对应角 .
平移的性质
答 案
平移前后图形全等,线段AB平移后为线段 ,则AB平行且等于 .平移前后,点A的对应点为点 ,点B的对应点为点 ,点C的对应点为 ,则AA'平行且等于
或 .
A'B'
A'
C'
B'
讲 解
笔 记
A'B'
BB'
CC'
平行
平行
相等
相等
相等
平移的性质
【示例1】如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A. 8 B.10
C. 12 D.14
答 案
C
分析:平移前后,图形全等,则△ABC≌ ,所以AC= ,BC= ,根据平移的性质,可以得到AD= = ,四边形ABFD的周长为AB+BF+DF+AD=AB+BC+ +DF+AD,而AB+BF+
DF恰为 的周长,因△ABC平移1个单位得到△DEF,则AD=CF= ,所以四边形ABFD的周长为 .
△DEF
DF
EF
BE
CF
CF
△ABC
1
10+1+1=12
平移的对应元素:
对应点、对应角、对应线段
总 结
平移的性质
例3
答 案
如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( )
A. 16cm B. 18cm
C. 20cm D. 22cm
C
解 析
例3
根据题意,将周长为16cm的△ABC沿BC向右平移2cm得到△DEF,
∴AD=CF=2cm,BF=BC+CF=BC=2cm,DF=AC;
又∵AB+BC+AC=16cm,
∴四边形ABFD的周长
=AD+AB+BF+DF=2+AB+BC+2+AC
=20cm
解 析
练习3.1
答 案
将线段AB平移1cm,得到线段A'B',则点A到点A'的距离
是 cm.
1
解 析
在平移的过程中各点的运动状态是一样的,现在将线段平移1cm,则每一点都平移1cm,
即AA'=1cm,
∴点A到点A'的距离是1cm.
练习3.2
答 案
如图,已知线段AB的长度为2cm,将线段AB向下平移2.5cm后得到线段A'B',连接AA',BB',则四边形AA'B'B的周长为( )
A. 4.5cm
B. 8cm
C. 9cm
D. 10cm
C
练习3.3
答 案
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿着水平方向向右平移后得到△DEF,若F为BC的中点,则四边形ABED的面积为( )
A. 12 B. 24
C. 48 D. 60
B
解 析
练习3.3
由平移的性质可知,FE=BC=8,四边形ABED为平行四边形,
∵F为BC的中点,
∴BF=4,
∴BE=FE=FB=4,
∴四边形ABED的面积=4×6=24
故选B
解 析
分析:△ABC向右平移2个单位,再向上平移3个单位,可以理解为点A、点B、点C分别向 平移 个单位,再向 平移
个单位后变为点A1、点B1、点C1,
确定后连接各点即为△A1B1C1的位置;
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(1)△ABC的顶点都在方格纸的格点上,
先将△ABC向右平移2个单位,再向上平移
3个单位,得到△A1B1C1,其中点A1,B1,
C1分别是A,B,C的对应点,试画出△1B1C1;
平移的性质
答 案
右
2
3
B1
A1
C1
上
思路点拨
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(2)连接AA1、BB1,则线段AA1、BB1的位置关系为 ,线段AA1、BB1的数量关系为 ;
平移的性质
答 案
平行
相等
【示例】如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
(3)△A1B1C1的面积为 .(平方单位).
(3)若以线段A1C1的长度为 作为底,
则△A1B1C1高为 ,面积为 .
平移的性质
答 案
3
2
3
3
思路点拨
平移画图步骤:
1.找到原图形中的关键点
2.根据平移的方向和平移的距离,画出对应点
3.连接对应点,画出图形
总 结
平移的性质
例4
答 案
为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至A'的位置,使点A与A'对应,得到△A'B'C';
例5
根据网格结构找出点B、C平移后的对应点B'、C'的位置,再与点A'顺次连接即可.
答 案
解 析
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(2)线段AA'与BB'的关系是: ;
答 案
平行且相等
解 析
根据平移的性质解答;
例5
如图,在边长为1个单位长度的小正方形组成的网格中.
(3)求△ABC的面积;
答 案
解 析
利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解
△ABC的面积
图形的旋转
旋转的概念和性质
引入
观察上面图片,你能发现都在做什么动作吗?
在平面内,将一个图形绕一个一个定点按某个方向转动一个角度,图形的这种变化称为 ,这个定点称为 ,转动的角称为 .
讲 解
旋转
旋转中心
旋转角
如图,△ABC≌ ,点A旋转到了点 ,∠AOD= .
= ,BO= ,AO= ,CO= .
△DEF
D
∠BOE
∠COF
EO
FO
DO
旋转的概念和性质
旋转不改变图形的 和 .
一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离 ,任何一组对应点与旋转中心的连线所成的角都等于 ;对应线段相等,对应角相等.
笔 记
形状
大小
旋转的概念和性质
相等
旋转角
将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
答 案
旋转的概念和性质
旋转时需注意顺时针方向还是逆时针方向
注意
单步训练
B
【示例】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,此时点C恰好在线段DE上,若∠B=40°,∠CAE=60°,则∠DAC的度数为( )
A.15° B.20°
C.25° D.30°
分析:旋转前后图形全等,所以△ABC≌ ,∠B= ,AE= ,因∠CAE=60°,所以∠ACE= ,因∠B=40°,,则∠DAC=∠ACE- =60°- = .
答 案
△ADE
∠D
旋转中的边角计算
思路点拨
AC
60°
∠D
60°
20°
B
先确定旋转中心、旋转角度、旋转方向,再根据边角关系计算.
总结
旋转中的边角计算
先确定旋转中心、旋转角度、旋转方向,再根据边角关系计算.
总结
例6
答 案
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A.70° B.80°
C.84° D.86°
B
解 析
有旋转的性质可知:∠B=∠AB1C1,AB=AB1,∠BAB1=100°.
∵AB=AB1,∠BAB1=100°
∴∠B=∠BB1A=40°
∴∠AB1C1=40°
∴∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°
练习6.1
答 案
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1=20°,则∠B= 度.
65
解 析
∵Rt△ABC绕直角顶点C顺时针
旋转90°,得到△A'B'C',
∴∠ACA'=90°,CA=CA',∠B=∠CB'A',
∴△CAA'=45°,
∵∠CB'A'=∠B'AC+∠1=45°+20°=65°
∴∠B=65°.
【示例】已知:如图,△A'B'C'是由△ABC以点O为中心经过一次旋转得到的,点A'、B'、C'分别是点A、B、C旋转后的对应点.
求作:旋转中心O.
分析:找图形旋转中心的步骤:
1.先找到原图形和旋转后图形的两组对应点;
2.连接两组对应点,出现两条线段,分别作这两条线段的 ,则这两条 的交点就是 .
已知旋转前后图形,确定旋转中心
答 案
垂直平分线
旋转中心
思路点拨
O
垂直平分线
【示例】已知△ABC,如图,请画出以点C为旋转中心,旋转角为30°,按顺时针方向旋转后的图形△A'B'C'.(用直尺和量角器即可)
已知旋转前后图形,确定旋转中心
画旋转图形的步骤:
1.确定旋转中心、旋转方向、旋转角度
2.选取关键点,以旋转中心为圆心,沿题中的方向和角度分别作出各关键点的对应点
3.顺次连接作出的对应点,即为旋转后图形
总结
(1)在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是( )
A.点A B.点B C.点C D.点D
例7
答 案
B
(2)画出△ABC绕点 C顺时针旋转90°后的图形△A'B'C.
例7
答 案
中心对称
中心对称
引入
生活中的阴阳八卦图、剪纸等,都和旋转有着密不可分的关系,那这两个图都可由自身的一部分旋转多少度得到呢?
中心对称
答 案
讲 解
在平面内,如果把一个图形绕某个点旋转 后,能与另一个图形重合,那么就说这两个图形关于这个点成 ,这个点叫 .
在平面内,把一个图形绕某个点旋转 后,如果旋转前后的图形互相重合,那么这个图形叫做 ,这个点就是它的 .
成中心对称的两个图形中,对应点的连线经过 ,且被对称中心 .
总结
180°
中心对称
对称中心
180°
中心对称图形
对称中心
对称中心
平分
【示例】观察下列汽车标志,其中是中心对称图形的是( )
答 案
中心对称图形
图形旋转180°后不变的即为中心对称图形
注意
C
下列图案中,可以看作中心对称图形的是( )
A. B. C. D.
答 案
例8
C
在以下回收、绿色食品、节能、节水四个标志中,是中心对称图形的是( )
A. B. C. D.
答 案
练习8.1
D
【示例】如图,已知△ABC和点O,在图中画出△A'B'C',使△ABC与△A'B'C'关于O点中心对称.
答 案
中心对称图形
思路点拨
连接AO、BO、CO并延长,再截取等线段
找到对应点,连接各对应点即为中心对称后图形
【示例】如图所示的两个图形成中心对称,请找出它的对称中心
答 案
中心对称图形
两图形成中心对称,则对应点连线的交点即为对称中心
总结
总结
中心对称图形
例9
答 案
在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成
中心对称的△A1B1C1,再把向上
平移4个单位长度得到△A2B2C2
例9
答 案
如图所示
例9
答 案
在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(2)△A2B2C2与△ABC是否
关于某点成中心对称?若是,
直接写出对称中心的坐标;若不是,
请说明理由.
由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
Thank you
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
