湘教版八年级上册数学第2章三角形单元复习检测卷(含答案)
文档属性
| 名称 | 湘教版八年级上册数学第2章三角形单元复习检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 849.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-08 00:00:00 | ||
图片预览



文档简介
第2章达标检测卷
一、选择题(每题3分,共30分)
1.在下列长度的四根木棒中,能与4 cm,9 cm长的两根木棒钉成一个三角形的是( )
A.4 cm B.5 cm C.9 cm D.13 cm
2.如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
3.如图,已知AC=DB,AB=DC,你认为证明△ABC≌△DCB应该用( )
A.“边边边” B.“边角边” C.“角边角” D.“角角边”
4.已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD与∠CBD之间的关系为( )
A.∠CAD=∠CBD
B.∠CAD>∠CBD
C.∠CAD<∠CBD
D.不能确定
5.下列命题是假命题的是( )
A.有两个角为60°的三角形是等边三角形
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
6.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,
∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
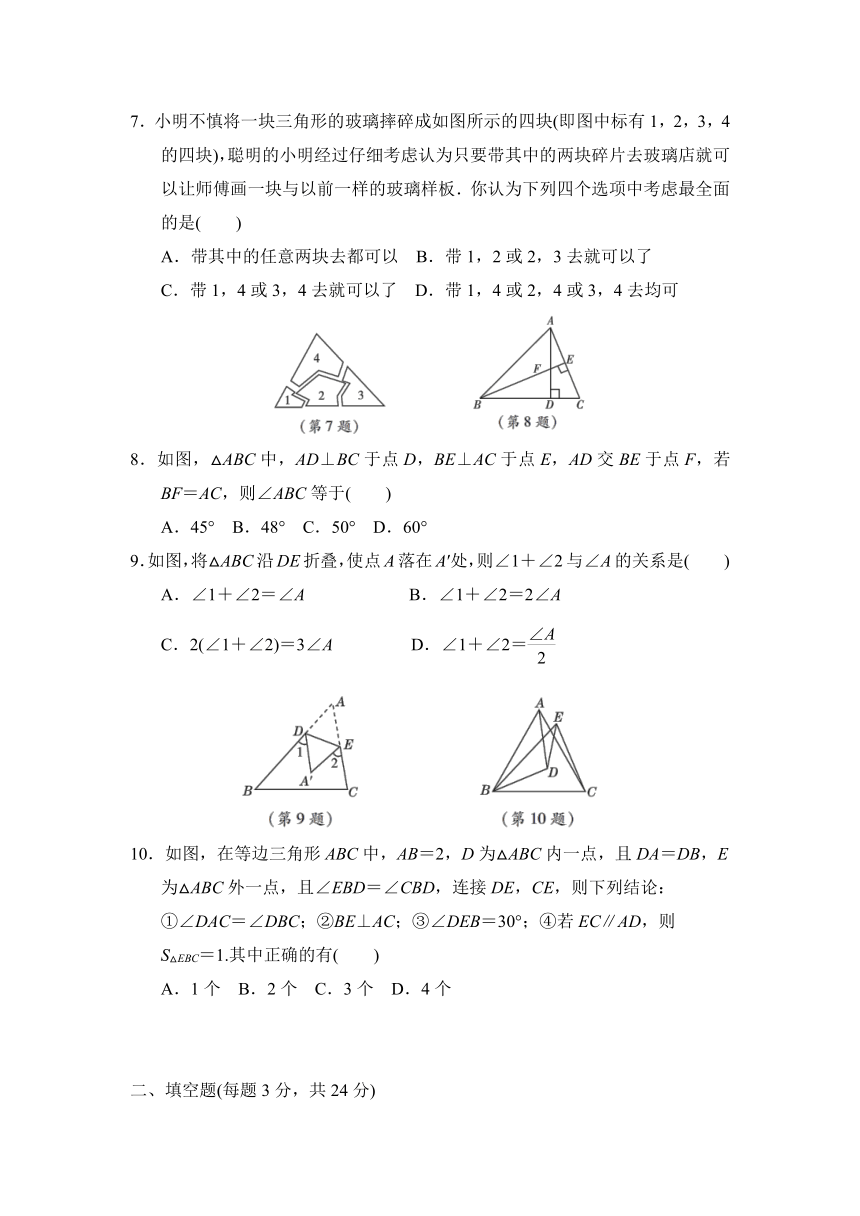
7.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),聪明的小明经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个选项中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了 D.带1,4或2,4或3,4去均可
8.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD交BE于点F,若BF=AC,则∠ABC等于( )
A.45° B.48° C.50° D.60°
9.如图,将△ABC沿DE折叠,使点A落在A′处,则∠1+∠2与∠A的关系是( )
A.∠1+∠2=∠A B.∠1+∠2=2∠A
C.2(∠1+∠2)=3∠A D.∠1+∠2=
10.如图,在等边三角形ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,且∠EBD=∠CBD,连接DE,CE,则下列结论:
①∠DAC=∠DBC;②BE⊥AC;③∠DEB=30°;④若EC∥AD,则
S△EBC=1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.命题“同角的余角相等”的条件是________________________,结论是____________________.
12.如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是________________.(写出一个即可)
13.已知等腰三角形的一个内角是80°,则它的底角是________.
14.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为________.
15.如图,在△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠CDF=________.
16.如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
17.如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于点D,CE⊥PQ于点E,且AD=2 cm,DB=3 cm,则梯形ADEC的面积是________.
18.如图,已知∠AOB=α,在射线OA,OB上分别取点A1,B1,使OA1=OB1,连接A1B1,在B1A1,B1B上分别取点A2,B2,使B1B2=B1A2,连接A2B2……按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则(1)θ1=________;(2)θn=__________________.
三、解答题(19题6分,20,21题每题8分,22,23题每题10分,24,25题每题12分,共66分)
19.如图,点F是△ABC的边BC的延长线上一点,DF⊥AB,∠A=30°,
∠F=40°,求∠ACF的度数.
20.已知a,b,c是△ABC的三边长,a=4,b=6,若三角形的周长是小于18的偶数.
(1)求边长c;
(2)判断△ABC的形状.
21.如图,已知点E、C在线段BF上,且BE=CF,CM∥DF.
(1)作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:AC=DF.
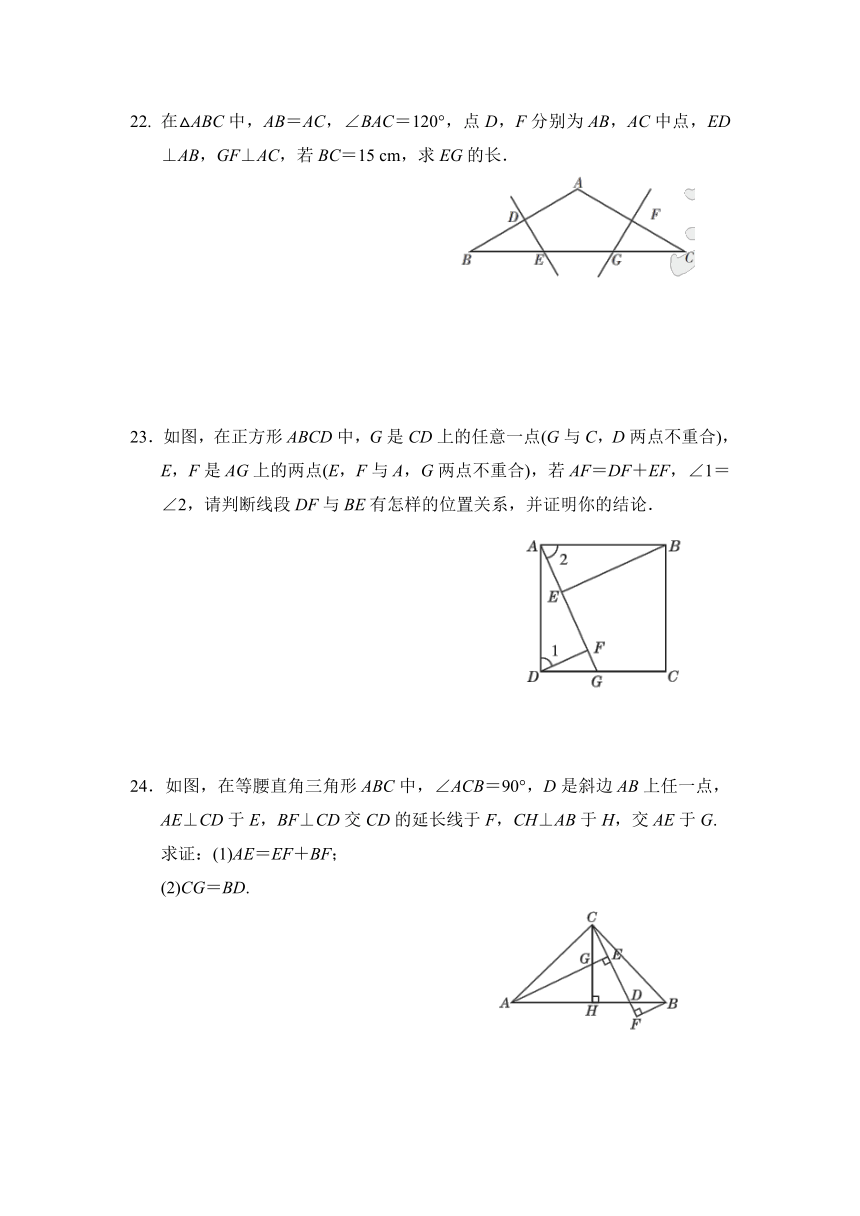
22. 在△ABC中,AB=AC,∠BAC=120°,点D,F分别为AB,AC中点,ED⊥AB,GF⊥AC,若BC=15 cm,求EG的长.
23.如图,在正方形ABCD中,G是CD上的任意一点(G与C,D两点不重合),E,F是AG上的两点(E,F与A,G两点不重合),若AF=DF+EF,∠1=∠2,请判断线段DF与BE有怎样的位置关系,并证明你的结论.
24.如图,在等腰直角三角形ABC中,∠ACB=90°,D是斜边AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H,交AE于G.
求证:(1)AE=EF+BF;
(2)CG=BD.
25.如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由.
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合),并说明理由.
答案
一、1.C 点拨:根据三角形三边关系知:5 cm<第三边的长<13 cm,只有C选项符合.
2.B 3.A
4.A 点拨:根据MN是线段AB的垂直平分线,C,D是MN上任意两点,可知∠CAD与∠CBD关于直线MN对称,所以∠CAD=∠CBD.
5.D
6. A 点拨:∵等边三角形ABC中,AD⊥BC,
∴BD=CD,即AD是BC的垂直平分线.
∵点E在线段AD上,
∴BE=CE,
∴∠EBC=∠ECB=45°.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB-∠ECB=15°.
7.D
8.A 点拨:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠BEA=90°,
∴∠FBD+∠BFD=90°.
又∵∠AFE+∠CAD=90°,∠BFD=∠AFE,
∴∠FBD=∠CAD,
在△FDB和△CDA中,
∴△FDB≌△CDA,
∴DA=DB,
∴∠ABC=∠BAD=45°.
9.B 点拨:连接AA′,易知DA=DA′,EA=EA′,
∴∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1=∠DAA′+∠DA′A=2∠DAA′,∠2=∠EAA′+∠EA′A=2∠EAA′,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC.
10.A
二、11.两个角是同角的余角;这两个角相等
12.AB=AC(答案不唯一)
13.50°或80°
14.4
15.74° 点拨:∵∠A=40°,∠B=72°,
∴∠ACB=68°.
∵CE平分∠ACB,CD⊥AB于点D,
∴∠BCE=34°,∠BCD=90°-72°=18°.
∵DF⊥CE,
∴∠CDF=90°-∠FCD=90°-(∠BCE-∠BCD)=90°-(34°-18°)=74°.
16.6
17.12.5 cm2 点拨:由条件易证明△ADB≌△BEC(AAS),所以AD=BE=2 cm,DB=CE=3 cm,然后利用梯形的面积公式求解即可.
18.(1)
(2)
点拨:∵OB1=OA1,∠AOB=α,
∴∠A1B1O =(180°-α),
∴θ1=180°-∠A1B1O=;同理可求得θ2==;
θ3==……依上述规律知θn=.
三、19.解:∵DF⊥AB,
∴∠FDB=90°.
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.
20.解:(1)因为a=4,b=6,所以周长l的取值范围为12(2)当c=6时,b=c,△ABC为等腰三角形;当c=4时,a=c,△ABC为等腰三角形.综上,△ABC是等腰三角形.
21.(1)解:如图.
(2)证明:∵CM∥DF,
∴∠MCE=∠F,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF,
∴AC=DF.
22.解:如图,连接AE,AG,
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B=×(180°-120°)=30°,
∴∠BAE=30°,
∴∠AEG=60°.
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG.
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又∵BE+EG+GC=BC=15 cm,
∴EG=5 cm.
23.解:DF∥BE.证明如下.
∵四边形ABCD是正方形,
∴AB=AD,∠DAF+∠2=90°.
∵AF=AE+EF,AF=DF+EF,
∴AE=DF.
在△ABE和△DAF中,
∴△ABE≌△DAF(SAS).
∴∠AEB=∠DFA,∠ABE=∠DAF.
∴∠BEF=∠2+∠ABE=∠2+∠DAF=90°.
∴∠BEF=∠AEB=∠DFA=90°.
∴DF∥BE(内错角相等,两直线平行).
24.证明:(1)∵∠ACB=90°,
即∠ACE+∠BCF=90°.
又BF⊥CD于F,
∴∠BCF+∠CBF=90°.
∴∠ACE=∠CBF.
又∵AE⊥CD于E,BF⊥CD于F.
∴∠AEC=∠CFB=90°.
∵△ACB是等腰直角三角形,且∠ACB=90°,
∴AC=CB.
在△ACE与△CBF中,
∴△ACE≌△CBF(AAS).
∴AE=CF,CE=BF.
∴CF=CE+EF=BF+EF=AE,即AE=EF+BF.
(2)证法一:∵CH⊥AB于H,
∴∠CDH+∠DCH=90°,又∠BDF+∠FBD=90°,且∠CDH=∠BDF,
∴∠ECG=∠FBD.
由(1)知,CE=BF.
在△CEG与△BFD中,
∴△CEG≌△BFD(ASA),
∴CG=BD.
证法二:∵CH是等腰直角三角形ABC斜边上的高线,
∴∠ACG=45°.
又∠CBA=∠CAB=45°,
∴∠ACG=∠CBD.
由(1)知,△ACE ≌△CBF,
∴∠CAG=∠BCD.
在△ACG与△CBD中,
∴△ACG≌△CBD(ASA),
∴CG=BD.
25.解:(1)①CF⊥BD;CF=BD
②当点D在线段BC的延长线上时,①中的结论仍然成立.
理由:由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,
∴∠DAF=∠BAC.
∴∠DAB=∠FAC.
又∵AB=AC,
∴△DAB≌△FAC.
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形.
∴∠ABC=∠ACB=45°.
∴∠ACF=45°.
∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BC.
理由:如图,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,
∴∠ACB=∠AGC=45°,
∴△AGC是等腰直角三角形,∴AC=AG.
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
一、选择题(每题3分,共30分)
1.在下列长度的四根木棒中,能与4 cm,9 cm长的两根木棒钉成一个三角形的是( )
A.4 cm B.5 cm C.9 cm D.13 cm
2.如图,△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
3.如图,已知AC=DB,AB=DC,你认为证明△ABC≌△DCB应该用( )
A.“边边边” B.“边角边” C.“角边角” D.“角角边”
4.已知MN是线段AB的垂直平分线,C,D是MN上任意两点,则∠CAD与∠CBD之间的关系为( )
A.∠CAD=∠CBD
B.∠CAD>∠CBD
C.∠CAD<∠CBD
D.不能确定
5.下列命题是假命题的是( )
A.有两个角为60°的三角形是等边三角形
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
6.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,
∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),聪明的小明经过仔细考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个选项中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1,2或2,3去就可以了
C.带1,4或3,4去就可以了 D.带1,4或2,4或3,4去均可
8.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD交BE于点F,若BF=AC,则∠ABC等于( )
A.45° B.48° C.50° D.60°
9.如图,将△ABC沿DE折叠,使点A落在A′处,则∠1+∠2与∠A的关系是( )
A.∠1+∠2=∠A B.∠1+∠2=2∠A
C.2(∠1+∠2)=3∠A D.∠1+∠2=
10.如图,在等边三角形ABC中,AB=2,D为△ABC内一点,且DA=DB,E为△ABC外一点,且∠EBD=∠CBD,连接DE,CE,则下列结论:
①∠DAC=∠DBC;②BE⊥AC;③∠DEB=30°;④若EC∥AD,则
S△EBC=1.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.命题“同角的余角相等”的条件是________________________,结论是____________________.
12.如图,已知∠B=∠C,添加一个条件使△ABD≌△ACE(不标注新的字母,不添加新的线段),你添加的条件是________________.(写出一个即可)
13.已知等腰三角形的一个内角是80°,则它的底角是________.
14.如图,△ABC的周长为18,且AB=AC,AD⊥BC于D,△ACD的周长为13,那么AD的长为________.
15.如图,在△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于点D,DF⊥CE于点F,则∠CDF=________.
16.如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
17.如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于点D,CE⊥PQ于点E,且AD=2 cm,DB=3 cm,则梯形ADEC的面积是________.
18.如图,已知∠AOB=α,在射线OA,OB上分别取点A1,B1,使OA1=OB1,连接A1B1,在B1A1,B1B上分别取点A2,B2,使B1B2=B1A2,连接A2B2……按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则(1)θ1=________;(2)θn=__________________.
三、解答题(19题6分,20,21题每题8分,22,23题每题10分,24,25题每题12分,共66分)
19.如图,点F是△ABC的边BC的延长线上一点,DF⊥AB,∠A=30°,
∠F=40°,求∠ACF的度数.
20.已知a,b,c是△ABC的三边长,a=4,b=6,若三角形的周长是小于18的偶数.
(1)求边长c;
(2)判断△ABC的形状.
21.如图,已知点E、C在线段BF上,且BE=CF,CM∥DF.
(1)作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,求证:AC=DF.
22. 在△ABC中,AB=AC,∠BAC=120°,点D,F分别为AB,AC中点,ED⊥AB,GF⊥AC,若BC=15 cm,求EG的长.
23.如图,在正方形ABCD中,G是CD上的任意一点(G与C,D两点不重合),E,F是AG上的两点(E,F与A,G两点不重合),若AF=DF+EF,∠1=∠2,请判断线段DF与BE有怎样的位置关系,并证明你的结论.
24.如图,在等腰直角三角形ABC中,∠ACB=90°,D是斜边AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H,交AE于G.
求证:(1)AE=EF+BF;
(2)CG=BD.
25.如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.
(1)如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图②,线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图③,①中的结论是否仍然成立,并说明理由.
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C,F不重合),并说明理由.
答案
一、1.C 点拨:根据三角形三边关系知:5 cm<第三边的长<13 cm,只有C选项符合.
2.B 3.A
4.A 点拨:根据MN是线段AB的垂直平分线,C,D是MN上任意两点,可知∠CAD与∠CBD关于直线MN对称,所以∠CAD=∠CBD.
5.D
6. A 点拨:∵等边三角形ABC中,AD⊥BC,
∴BD=CD,即AD是BC的垂直平分线.
∵点E在线段AD上,
∴BE=CE,
∴∠EBC=∠ECB=45°.
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACE=∠ACB-∠ECB=15°.
7.D
8.A 点拨:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠BEA=90°,
∴∠FBD+∠BFD=90°.
又∵∠AFE+∠CAD=90°,∠BFD=∠AFE,
∴∠FBD=∠CAD,
在△FDB和△CDA中,
∴△FDB≌△CDA,
∴DA=DB,
∴∠ABC=∠BAD=45°.
9.B 点拨:连接AA′,易知DA=DA′,EA=EA′,
∴∠DAA′=∠DA′A,∠EAA′=∠EA′A,
∴∠1=∠DAA′+∠DA′A=2∠DAA′,∠2=∠EAA′+∠EA′A=2∠EAA′,
∴∠1+∠2=2(∠DAA′+∠EAA′)=2∠BAC.
10.A
二、11.两个角是同角的余角;这两个角相等
12.AB=AC(答案不唯一)
13.50°或80°
14.4
15.74° 点拨:∵∠A=40°,∠B=72°,
∴∠ACB=68°.
∵CE平分∠ACB,CD⊥AB于点D,
∴∠BCE=34°,∠BCD=90°-72°=18°.
∵DF⊥CE,
∴∠CDF=90°-∠FCD=90°-(∠BCE-∠BCD)=90°-(34°-18°)=74°.
16.6
17.12.5 cm2 点拨:由条件易证明△ADB≌△BEC(AAS),所以AD=BE=2 cm,DB=CE=3 cm,然后利用梯形的面积公式求解即可.
18.(1)
(2)
点拨:∵OB1=OA1,∠AOB=α,
∴∠A1B1O =(180°-α),
∴θ1=180°-∠A1B1O=;同理可求得θ2==;
θ3==……依上述规律知θn=.
三、19.解:∵DF⊥AB,
∴∠FDB=90°.
∵∠F=40°,∠FDB+∠F+∠B=180°,
∴∠B=50°.在△ABC中,
∵∠A=30°,∠B=50°,
∴∠ACF=30°+50°=80°.
20.解:(1)因为a=4,b=6,所以周长l的取值范围为12
21.(1)解:如图.
(2)证明:∵CM∥DF,
∴∠MCE=∠F,
∵BE=CF,
∴BE+CE=CF+CE,
即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF,
∴AC=DF.
22.解:如图,连接AE,AG,
∵D为AB中点,ED⊥AB,
∴EB=EA,
∴△ABE为等腰三角形,
又∵∠B=×(180°-120°)=30°,
∴∠BAE=30°,
∴∠AEG=60°.
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG.
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又∵BE+EG+GC=BC=15 cm,
∴EG=5 cm.
23.解:DF∥BE.证明如下.
∵四边形ABCD是正方形,
∴AB=AD,∠DAF+∠2=90°.
∵AF=AE+EF,AF=DF+EF,
∴AE=DF.
在△ABE和△DAF中,
∴△ABE≌△DAF(SAS).
∴∠AEB=∠DFA,∠ABE=∠DAF.
∴∠BEF=∠2+∠ABE=∠2+∠DAF=90°.
∴∠BEF=∠AEB=∠DFA=90°.
∴DF∥BE(内错角相等,两直线平行).
24.证明:(1)∵∠ACB=90°,
即∠ACE+∠BCF=90°.
又BF⊥CD于F,
∴∠BCF+∠CBF=90°.
∴∠ACE=∠CBF.
又∵AE⊥CD于E,BF⊥CD于F.
∴∠AEC=∠CFB=90°.
∵△ACB是等腰直角三角形,且∠ACB=90°,
∴AC=CB.
在△ACE与△CBF中,
∴△ACE≌△CBF(AAS).
∴AE=CF,CE=BF.
∴CF=CE+EF=BF+EF=AE,即AE=EF+BF.
(2)证法一:∵CH⊥AB于H,
∴∠CDH+∠DCH=90°,又∠BDF+∠FBD=90°,且∠CDH=∠BDF,
∴∠ECG=∠FBD.
由(1)知,CE=BF.
在△CEG与△BFD中,
∴△CEG≌△BFD(ASA),
∴CG=BD.
证法二:∵CH是等腰直角三角形ABC斜边上的高线,
∴∠ACG=45°.
又∠CBA=∠CAB=45°,
∴∠ACG=∠CBD.
由(1)知,△ACE ≌△CBF,
∴∠CAG=∠BCD.
在△ACG与△CBD中,
∴△ACG≌△CBD(ASA),
∴CG=BD.
25.解:(1)①CF⊥BD;CF=BD
②当点D在线段BC的延长线上时,①中的结论仍然成立.
理由:由正方形ADEF得AD=AF,∠DAF=90°.
∵∠BAC=90°,
∴∠DAF=∠BAC.
∴∠DAB=∠FAC.
又∵AB=AC,
∴△DAB≌△FAC.
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴△ABC是等腰直角三角形.
∴∠ABC=∠ACB=45°.
∴∠ACF=45°.
∴∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BC.
理由:如图,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,
∴∠ACB=∠AGC=45°,
∴△AGC是等腰直角三角形,∴AC=AG.
又∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∴∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.
同课章节目录
