湘教版数学八年级上册第2章 三角形 达标测试卷(含答案)
文档属性
| 名称 | 湘教版数学八年级上册第2章 三角形 达标测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 88.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 07:07:20 | ||
图片预览


文档简介
湘教版数学八年级上册第2章达标测试卷
一、选择题(每题3分,共24分)
1.下列长度的三根木棒能组成三角形的是( )
A.3,4,8 B.4,4,8 C.5,6,10 D.6,7,14
2.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
3.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为( )
A.5 B.6 C.7 D.8
4.如图,已知线段AB,分别以A,B为圆心,大于AB的长为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,则∠BCM的度数为( )
A.40° B.50° C.60° D.70°
5.下列命题是假命题的是( )
A.有两个角为60°的三角形是等边三角形
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
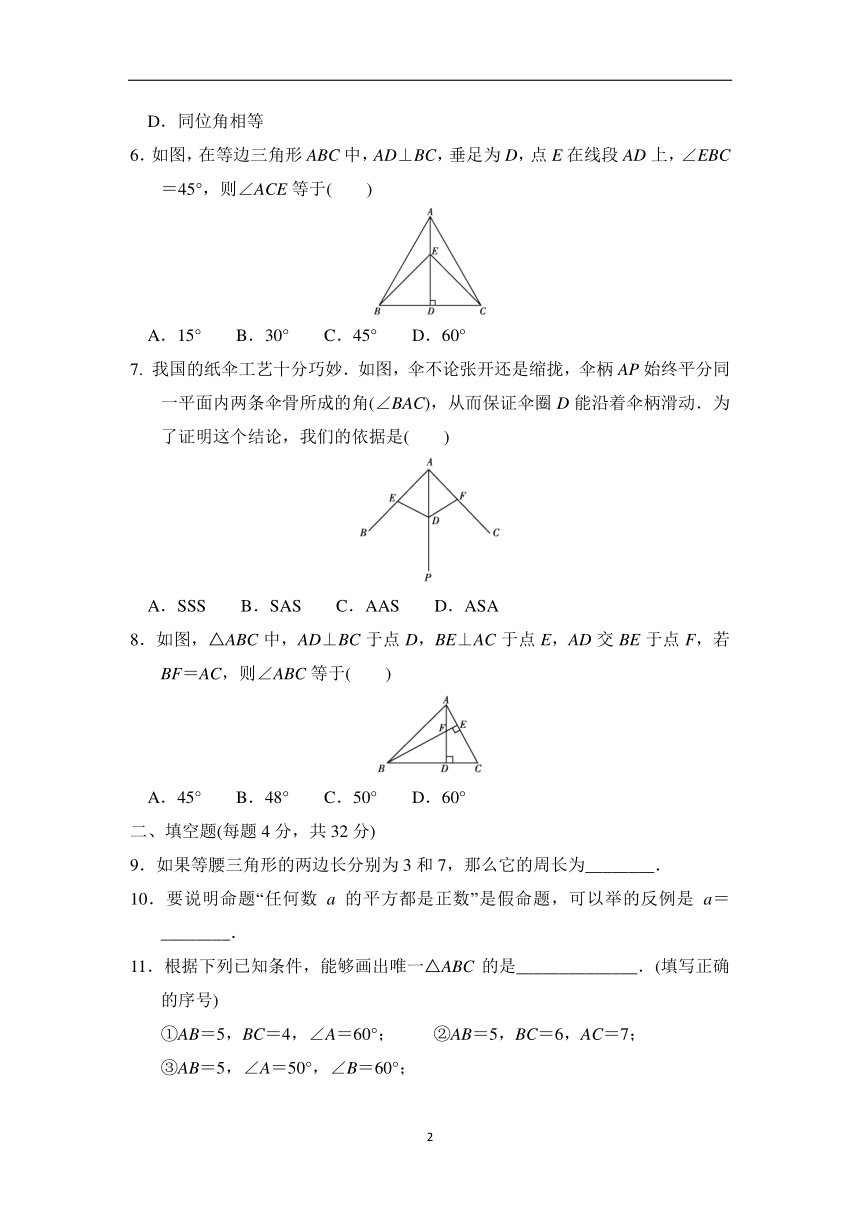
6.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
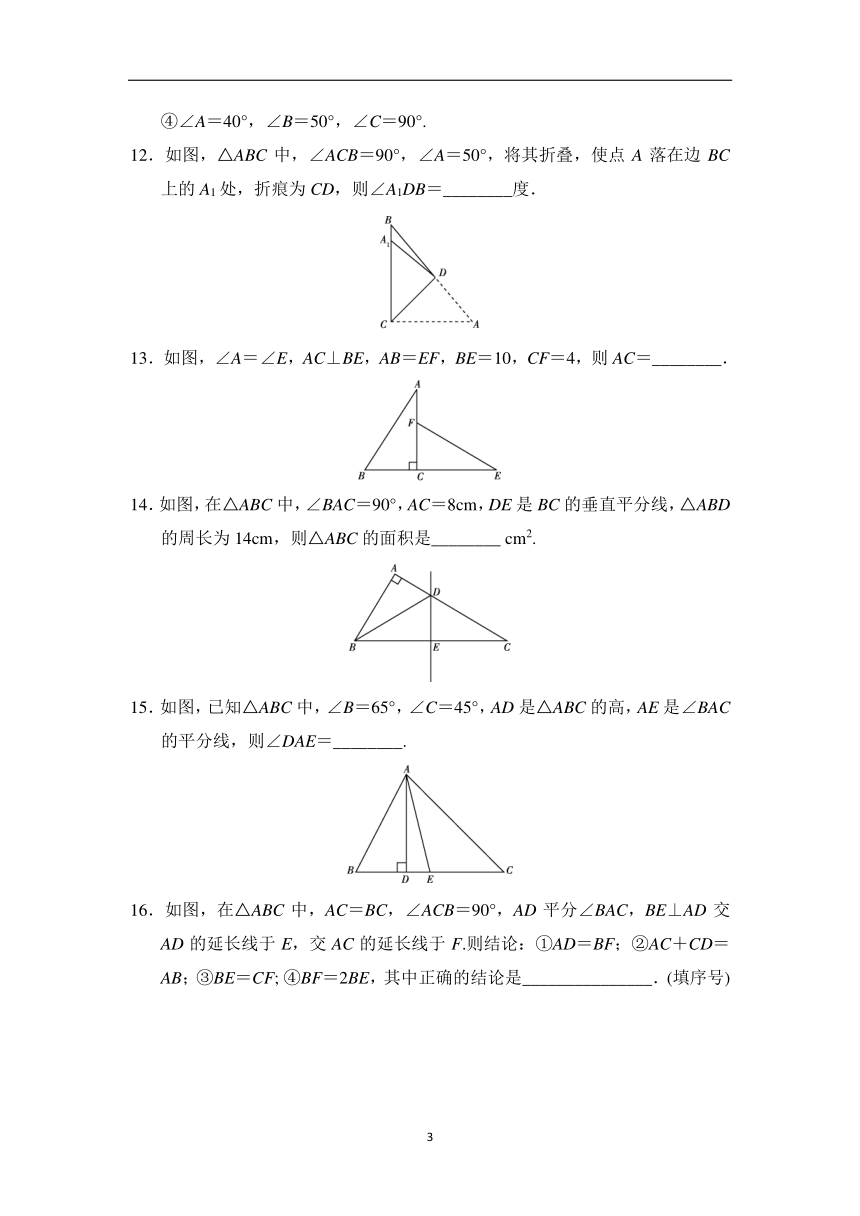
7. 我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角(∠BAC),从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
8.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD交BE于点F,若BF=AC,则∠ABC等于( )
A.45° B.48° C.50° D.60°
二、填空题(每题4分,共32分)
9.如果等腰三角形的两边长分别为3和7,那么它的周长为________.
10.要说明命题“任何数a的平方都是正数”是假命题,可以举的反例是a=________.
11.根据下列已知条件,能够画出唯一△ABC的是______________.(填写正确的序号)
①AB=5,BC=4,∠A=60°; ②AB=5,BC=6,AC=7;
③AB=5,∠A=50°,∠B=60°;
④∠A=40°,∠B=50°,∠C=90°.
12.如图,△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的A1处,折痕为CD,则∠A1DB=________度.
13.如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
14.如图,在△ABC中,∠BAC=90°,AC=8cm,DE是BC的垂直平分线,△ABD的周长为14cm,则△ABC的面积是________ cm2.
15.如图,已知△ABC中,∠B=65°,∠C=45°,AD是△ABC的高,AE是∠BAC的平分线,则∠DAE=________.
16.如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AD的延长线于E,交AC的延长线于F.则结论:①AD=BF;②AC+CD=AB;③BE=CF; ④BF=2BE,其中正确的结论是_______________.(填序号)
三、解答题(17~20题每题8分,21题12分,共44分)
17.如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,求∠ADC的度数.
18.如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
19.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,求证:DE=DF.
20. 如图,在△ABC中,AB=AC,∠BAC=120°,点D,F分别为AB,AC的中点,ED⊥AB,GF⊥AC,若BC=15cm,求EG的长.
21.已知:如图①,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
(1)求证:AD=BE.
(2)求∠AEB的度数.
(3)拓展探究:如图②,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①∠AEB的度数为________°;
②探索线段CM,AE,BE之间的数量关系为__________________.
答案
一、1.C 2.B 3.C 4.B 5.D
6.A 解析:∵在等边三角形ABC中,AD⊥BC,∴BD=CD,即AD是BC的垂直平分线.∴BE=CE,∴∠EBC=∠ECB=45°.∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACE=∠ACB-∠ECB=15°.
7.A 解析:根据伞的结构易知AE=AF,DE=DF,AD=AD,∴△ADE≌△ADF(SSS),∴∠DAE=∠DAF,即AP平分∠BAC.
8.A 解析:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=∠BEC=∠AEF=90°,∴∠FBD+∠BFD=90°,
∠AFE+∠CAD=90°,
又∵∠BFD=∠AFE,
∴∠FBD=∠CAD,
在△FDB和△CAD中,
∴△FDB≌△CDA,∴DA=DB,
∴∠ABC=∠BAD=45°.
二、9.17
解析:(1)若3为腰长,7为底边长,由于3+3<7,所以三角形不存在;
(2)若7为腰长,3为底边长,则符合三角形的两边之和大于第三边,所以这个三角形的周长为7+7+3=17.
10.0 11.②③ 12.10
13.6 解析:∵AC⊥BE,
∴∠ACB=∠ECF=90°,
在△ABC和△EFC中,
∴△ABC≌△EFC(AAS),
∴AC=EC,BC=CF=4.
∵EC=BE-BC=10-4=6,∴AC=EC=6.
14.24 解析:∵DE是BC的垂直平分线,∴BD=DC.
∵△ABD的周长为14cm,
∴BD+AD+AB=14cm,∴AB+AD+CD=14cm,∴AB+AC=14cm.
∵AC=8cm,∴AB=6cm.
∵∠BAC=90°,∴△ABC的面积是AB×AC=×6×8=24(cm2).
15.10°
16.①②④ 解析:∵AD平分∠BAC,∴∠BAE=∠FAE.∵BE⊥AD,∴∠AEB=∠AEF=90°,∴∠F+∠FAE=90°.∵∠ACB=90°,∴∠F+∠FBC=90°,∠BCF=∠ACD=90°,∴∠FBC=∠FAE.在△ACD和△BCF中,∴△ACD≌△BCF(ASA),∴AD=BF,CD=CF.在△AEB和△AEF中,
∴△AEB≌△AEF(ASA),∴AB=AF,BE=EF,∴BF=2BE.
∵CD≠EF,∴CF≠BE.
∵AC+CF=AF,∴AC+CD=AF,∴AC+CD=AB.∴正确的有①②④.
三、17.解:∵△ABD≌△CBD,∴∠C=∠A=80°,
∴∠ADC=360°-∠A-∠ABC-∠C=360°-80°-70°-80°=130°.
18.解:(1)∵在△ABD中,AD=BD,∴∠B=∠BAD.
∵∠ADC=∠B+∠BAD,∠ADC=80°,∴∠B=∠ADC=40°.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,∴∠C=180°-∠B-∠BAC=70°,
∴∠C=∠BAC,∴BA=BC,∴△ABC是等腰三角形.
19.证明:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵点D为BC的中点,∴DB=DC,
在△DBE和△DCF中,
∴△DBE≌DCF(AAS),∴DE=DF.
20.解:如图,连接AE,AG,
∵D为AB的中点,ED⊥AB,∴EB=EA,
∴∠B=∠BAE.
∵AB=AC,∠BAC=120°,
∴∠B=×(180°-120°)=30°,
∴∠BAE=30°,∴∠AEG=60°.
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG.
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又∵BE+EG+GC=BC=15 cm,
∴EG=5 cm.
21.(1)证明:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE.
(2)解:由(1)知△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
(3)①90 ②AE=BE+2CM
解析:(3)①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,
∠ACB=∠DCE=90°,
∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴∠BEC=∠ADC.
∵点A,D,E在同一直线上,
∴∠ADC=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
②由∠DCE=90°,CD=CE,CM⊥DE,易得CM=DM=EM,
∴DE=DM+EM=2CM.
∵△ACD≌△BCE(已证),
∴BE=AD,
∴AE=AD+DE=BE+2CM.
一、选择题(每题3分,共24分)
1.下列长度的三根木棒能组成三角形的是( )
A.3,4,8 B.4,4,8 C.5,6,10 D.6,7,14
2.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
3.如图,△ABC≌△BDE,若AB=12,ED=5,则CD的长为( )
A.5 B.6 C.7 D.8
4.如图,已知线段AB,分别以A,B为圆心,大于AB的长为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,则∠BCM的度数为( )
A.40° B.50° C.60° D.70°
5.下列命题是假命题的是( )
A.有两个角为60°的三角形是等边三角形
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
6.如图,在等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
7. 我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角(∠BAC),从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
8.如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD交BE于点F,若BF=AC,则∠ABC等于( )
A.45° B.48° C.50° D.60°
二、填空题(每题4分,共32分)
9.如果等腰三角形的两边长分别为3和7,那么它的周长为________.
10.要说明命题“任何数a的平方都是正数”是假命题,可以举的反例是a=________.
11.根据下列已知条件,能够画出唯一△ABC的是______________.(填写正确的序号)
①AB=5,BC=4,∠A=60°; ②AB=5,BC=6,AC=7;
③AB=5,∠A=50°,∠B=60°;
④∠A=40°,∠B=50°,∠C=90°.
12.如图,△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边BC上的A1处,折痕为CD,则∠A1DB=________度.
13.如图,∠A=∠E,AC⊥BE,AB=EF,BE=10,CF=4,则AC=________.
14.如图,在△ABC中,∠BAC=90°,AC=8cm,DE是BC的垂直平分线,△ABD的周长为14cm,则△ABC的面积是________ cm2.
15.如图,已知△ABC中,∠B=65°,∠C=45°,AD是△ABC的高,AE是∠BAC的平分线,则∠DAE=________.
16.如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AD的延长线于E,交AC的延长线于F.则结论:①AD=BF;②AC+CD=AB;③BE=CF; ④BF=2BE,其中正确的结论是_______________.(填序号)
三、解答题(17~20题每题8分,21题12分,共44分)
17.如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,求∠ADC的度数.
18.如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.
19.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,求证:DE=DF.
20. 如图,在△ABC中,AB=AC,∠BAC=120°,点D,F分别为AB,AC的中点,ED⊥AB,GF⊥AC,若BC=15cm,求EG的长.
21.已知:如图①,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
(1)求证:AD=BE.
(2)求∠AEB的度数.
(3)拓展探究:如图②,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①∠AEB的度数为________°;
②探索线段CM,AE,BE之间的数量关系为__________________.
答案
一、1.C 2.B 3.C 4.B 5.D
6.A 解析:∵在等边三角形ABC中,AD⊥BC,∴BD=CD,即AD是BC的垂直平分线.∴BE=CE,∴∠EBC=∠ECB=45°.∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACE=∠ACB-∠ECB=15°.
7.A 解析:根据伞的结构易知AE=AF,DE=DF,AD=AD,∴△ADE≌△ADF(SSS),∴∠DAE=∠DAF,即AP平分∠BAC.
8.A 解析:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠ADC=∠BEC=∠AEF=90°,∴∠FBD+∠BFD=90°,
∠AFE+∠CAD=90°,
又∵∠BFD=∠AFE,
∴∠FBD=∠CAD,
在△FDB和△CAD中,
∴△FDB≌△CDA,∴DA=DB,
∴∠ABC=∠BAD=45°.
二、9.17
解析:(1)若3为腰长,7为底边长,由于3+3<7,所以三角形不存在;
(2)若7为腰长,3为底边长,则符合三角形的两边之和大于第三边,所以这个三角形的周长为7+7+3=17.
10.0 11.②③ 12.10
13.6 解析:∵AC⊥BE,
∴∠ACB=∠ECF=90°,
在△ABC和△EFC中,
∴△ABC≌△EFC(AAS),
∴AC=EC,BC=CF=4.
∵EC=BE-BC=10-4=6,∴AC=EC=6.
14.24 解析:∵DE是BC的垂直平分线,∴BD=DC.
∵△ABD的周长为14cm,
∴BD+AD+AB=14cm,∴AB+AD+CD=14cm,∴AB+AC=14cm.
∵AC=8cm,∴AB=6cm.
∵∠BAC=90°,∴△ABC的面积是AB×AC=×6×8=24(cm2).
15.10°
16.①②④ 解析:∵AD平分∠BAC,∴∠BAE=∠FAE.∵BE⊥AD,∴∠AEB=∠AEF=90°,∴∠F+∠FAE=90°.∵∠ACB=90°,∴∠F+∠FBC=90°,∠BCF=∠ACD=90°,∴∠FBC=∠FAE.在△ACD和△BCF中,∴△ACD≌△BCF(ASA),∴AD=BF,CD=CF.在△AEB和△AEF中,
∴△AEB≌△AEF(ASA),∴AB=AF,BE=EF,∴BF=2BE.
∵CD≠EF,∴CF≠BE.
∵AC+CF=AF,∴AC+CD=AF,∴AC+CD=AB.∴正确的有①②④.
三、17.解:∵△ABD≌△CBD,∴∠C=∠A=80°,
∴∠ADC=360°-∠A-∠ABC-∠C=360°-80°-70°-80°=130°.
18.解:(1)∵在△ABD中,AD=BD,∴∠B=∠BAD.
∵∠ADC=∠B+∠BAD,∠ADC=80°,∴∠B=∠ADC=40°.
(2)△ABC是等腰三角形.
理由:∵∠B=40°,∠BAC=70°,∴∠C=180°-∠B-∠BAC=70°,
∴∠C=∠BAC,∴BA=BC,∴△ABC是等腰三角形.
19.证明:∵AB=AC,∴∠B=∠C.
∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.
∵点D为BC的中点,∴DB=DC,
在△DBE和△DCF中,
∴△DBE≌DCF(AAS),∴DE=DF.
20.解:如图,连接AE,AG,
∵D为AB的中点,ED⊥AB,∴EB=EA,
∴∠B=∠BAE.
∵AB=AC,∠BAC=120°,
∴∠B=×(180°-120°)=30°,
∴∠BAE=30°,∴∠AEG=60°.
同理可证:∠AGE=60°,
∴△AEG为等边三角形,
∴AE=EG=AG.
又∵AE=BE,AG=GC,
∴BE=EG=GC,
又∵BE+EG+GC=BC=15 cm,
∴EG=5 cm.
21.(1)证明:∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴AD=BE.
(2)解:由(1)知△ACD≌△BCE,
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°,∴∠BEC=120°,
∴∠AEB=∠BEC-∠CED=120°-60°=60°.
(3)①90 ②AE=BE+2CM
解析:(3)①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,
∠ACB=∠DCE=90°,
∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),
∴∠BEC=∠ADC.
∵点A,D,E在同一直线上,
∴∠ADC=180°-45°=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
②由∠DCE=90°,CD=CE,CM⊥DE,易得CM=DM=EM,
∴DE=DM+EM=2CM.
∵△ACD≌△BCE(已证),
∴BE=AD,
∴AE=AD+DE=BE+2CM.
同课章节目录
