江苏省滨海县苏科版八年级数学下册讲义——9.4矩形、菱形、正方形(构造直角三角形斜边中线,附答案)
文档属性
| 名称 | 江苏省滨海县苏科版八年级数学下册讲义——9.4矩形、菱形、正方形(构造直角三角形斜边中线,附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 00:09:41 | ||
图片预览




文档简介
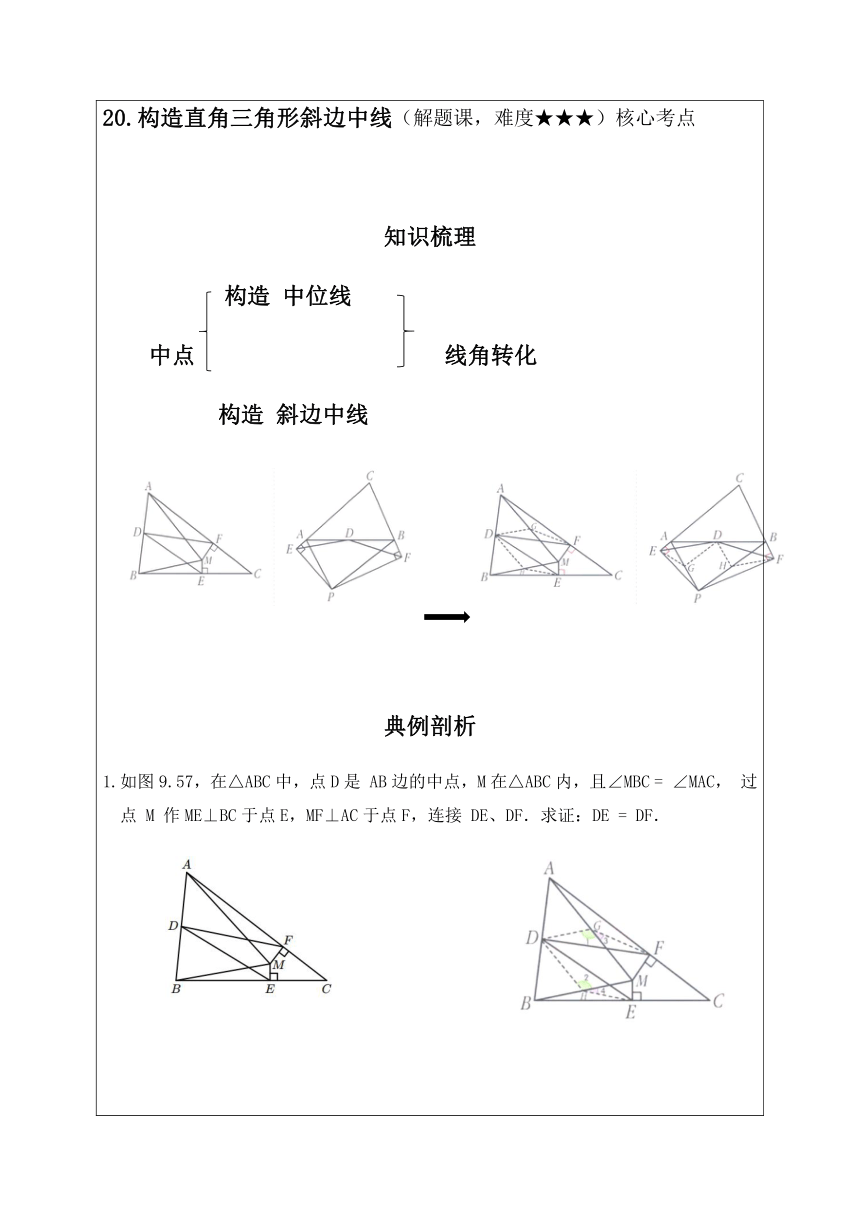
20.构造直角三角形斜边中线(解题课,难度★★★)核心考点
知识梳理
构造 中位线
中点 线角转化
构造 斜边中线
典例剖析
1.如图9.57,在△ABC中,点D是 AB边的中点,M在△ABC内,且∠MBC = ∠MAC, 过点 M 作ME⊥BC于点E,MF⊥AC于点F,连接 DE、DF.求证:DE = DF.
证明:取AM中点G, BM中点H, 连接 DG、DH、FG、EH,∵D是AB中点,ME⊥BC. MF⊥AC
∴DH=AM=FG, DG=BM =EH, DG//BM, DH//AM, ∴四边形DGMH为平行四边形,
∴∠1=∠2, ∵GF=AM=AG, ∴∠MAF=∠GFA, ∠3=∠ MAF+∠GFA= 2∠MAF
同理,∠4=2∠MBE, ∠MAF=∠MBE, ∠3=∠4, ∴∠DGF=∠1+∠3=∠2+∠4 =∠DHE, 在△DHE与△FGD中
DH=FG
∠ DHE=∠DGF ,∴△DHE≌△FGD ,DE=DF
EH=DG
2. 在 △ABC 中,D为AB 的中点,分别延 CA、CB 到点E、F,使DE = DF.过 E、F
分别作CA、CB 的垂线,相交于P,连接 AP、BP.求证:∠PAE = ∠PBF.
证明:取AP中点G,BP中点H, 连接 DG、DH、FH、EG, ∵D是AB中点,PE⊥AE, PF丄BF
∴DH=AP=EG,DG=BP=FH,在△DEG与△FDH中
DG=FH
EG=DH ∴△DEG≌△FDH,∴∠DGE=∠DHF,
DE=DF
∵DG//BP ,∠1 =∠APB, 又∵DH//AP, ∠2=∠APB , ∴∠1=∠2
∴∠3 = ∠DGE -∠1= ∠DHF -∠2 =∠4, ∵∠3 = 2∠APE , ∴∠4= 2∠BPF
∴∠APE=∠BPF ,∵PE⊥AC,PF丄BC, ∴∠PAE=90?-∠APE,∠PBF=90?-∠BPF
∴∠PAE=∠PBF
基础练
1.已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA = BC, DA = DE,连接EC, 取EC的中点M,连接BM和DM证明:BM = DM.
⑴取AC, AE的中点F、Q,分别连接 PB、PM. QD、QM,下列相等关系错误的是( )
A. MP = DQ = AE B. QM = BP= AC C. QM = BP=CE
⑵下列关于角的条件中,可以用来进一步判定△QDM≌△PMB的条件的是( )
A. ∠DEA = ∠BCA = ∠BAC B. ∠CPM = ∠CAE = ∠MQE
⑶综上,判定△QDM≌△PMB 的依据是( ),进而得到BM = DM.
SAS B.HL
2.如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形,M、N分别是CE、CF的中点,连接EF, Q是EF的中点, CP丄EF于点P,求证:DP = DQ.
取AC的中点G连接NG, DG, NQ, MP
①欲证DP = DQ,只需要证明( )
∠NQD = ∠MPD B.∠NDQ = ∠MDP C. △DNQ≌△DMP
②NQ = ___ , MP=_____.
③欲证△NDM为等边三角形,只需证明( )
A.∠DNM = 60° B. ND = NM C. ND = NM, ∠DNM = 60°
④证明△NGD≌△NCM,GD=_____, CM =_____,
∠GNC =______°,∠NGD + ∠4 = ______?, ∠4 + ∠5 = ______?
证明△NGD≌△NCM的判断依据是_______
20.构造直角三角形斜边中线答案
基础练:1.①C ②B ③A
证明:取AC、CE的中点P、Q,分别连接PB、PM、QD、QM
在Rt△ABC中,P是斜边AC的中点, ∴BP =,
在Rt△CDE中,Q是斜边CE的中点
∴DQ = CE, ∵Q、M分别是△AEC中边CE、AE的中点, ∴QM∥AC, QM = AC
∵P、M分别是△AEC中边AC、AE的中点, ∴MP//CE, MP =CE
∴ MP = DQ= CE, QM = BP = AC ,∵QM //AC, ∴∠MQE = ∠ACE
∵PM∥CE ,∴∠APM = ∠ACE, ∠APM = ∠ACE = ∠MQE, ∵∠APB = ∠DQE = 90°
∴∠APM + ∠APB = ∠MQE+∠DQE, ∴∠MPB =∠DQM, ∴△QDM≌△PMB(SAS),∴BM = DM
2.①C ②CE; CE; ③ C;④ BC; CE; 60;240; 240; SAS.
取AC的中点G,连接NG, DG
①证△NGD≌△NCM
先证明NG = NC及△GNC为等边三角形.
∵点N、 G分别是CF、AC的中点
∴GN = AF, ∵△ACF为等边三角形
∴AC = CF = AF ∴GN = NC = CG
∴△GNC为等边三角形
再证明 ∠NGD = ∠5
∠1 = ∠2 = ∠GNC = 60°
∵点D是AB的中点 , ∴ GD = CB, GD//CB ∴∠3 +∠4 = 180°
∴∠1 +∠ 3 + ∠4 = 240° ,∴∠NGD + ∠4 = 240°
∵△BCE为等边三角形, ∴∠6 = 60°, BC = EC ,∠4 + ∠5 + ∠2 + ∠6 = 360°
∴∠4 + ∠5 = 240°,∴∠NGD = ∠5
证明GD= CM
点M是CE的中点,∴CM = CE, ∵GD = CB, CB = CE,∴GD = CM
∴△NGD≌△NCM(SAS)
②证等边三角形
∴ND = NM, ∠7 = ∠8, △NDM为等腰三角形 ∵∠GNC = 60°,∠7 + ∠9 = 60°
∴∠DNM = ∠8 + ∠9 = 60°, ∴△NDM为等边三角形
再证△NQD≌△MPD
连接NQ, MP ∵△NDM为等边三角形 , ND = MD
①证NQ = MP
∵点N、Q分别是FE、FC的中点, ∴ NQ = CE, NQ//CE
∵点M是EC的中点,CP丄EF, ∴MP = CE ,NQ = MP
②证 ∠DNQ = ∠DMP
∵点N、M分别是FE、CE的中点 , ∴MN//EF, ∠10 = ∠ll, ∠12 = ∠13
∵NQ//CE, ∴∠ll = ∠14, ∵PM = CE = ME, ∴∠13 = ∠14 (等边对等角)
∴∠10 = ∠12, 又∵∠DNM = ∠DMN = 60°,∴∠10 = ∠12
∴∠DNQ =∠DMP, ∴△NQD≌△MPD(SAS), ∴DP= DQ。
知识梳理
构造 中位线
中点 线角转化
构造 斜边中线
典例剖析
1.如图9.57,在△ABC中,点D是 AB边的中点,M在△ABC内,且∠MBC = ∠MAC, 过点 M 作ME⊥BC于点E,MF⊥AC于点F,连接 DE、DF.求证:DE = DF.
证明:取AM中点G, BM中点H, 连接 DG、DH、FG、EH,∵D是AB中点,ME⊥BC. MF⊥AC
∴DH=AM=FG, DG=BM =EH, DG//BM, DH//AM, ∴四边形DGMH为平行四边形,
∴∠1=∠2, ∵GF=AM=AG, ∴∠MAF=∠GFA, ∠3=∠ MAF+∠GFA= 2∠MAF
同理,∠4=2∠MBE, ∠MAF=∠MBE, ∠3=∠4, ∴∠DGF=∠1+∠3=∠2+∠4 =∠DHE, 在△DHE与△FGD中
DH=FG
∠ DHE=∠DGF ,∴△DHE≌△FGD ,DE=DF
EH=DG
2. 在 △ABC 中,D为AB 的中点,分别延 CA、CB 到点E、F,使DE = DF.过 E、F
分别作CA、CB 的垂线,相交于P,连接 AP、BP.求证:∠PAE = ∠PBF.
证明:取AP中点G,BP中点H, 连接 DG、DH、FH、EG, ∵D是AB中点,PE⊥AE, PF丄BF
∴DH=AP=EG,DG=BP=FH,在△DEG与△FDH中
DG=FH
EG=DH ∴△DEG≌△FDH,∴∠DGE=∠DHF,
DE=DF
∵DG//BP ,∠1 =∠APB, 又∵DH//AP, ∠2=∠APB , ∴∠1=∠2
∴∠3 = ∠DGE -∠1= ∠DHF -∠2 =∠4, ∵∠3 = 2∠APE , ∴∠4= 2∠BPF
∴∠APE=∠BPF ,∵PE⊥AC,PF丄BC, ∴∠PAE=90?-∠APE,∠PBF=90?-∠BPF
∴∠PAE=∠PBF
基础练
1.已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA = BC, DA = DE,连接EC, 取EC的中点M,连接BM和DM证明:BM = DM.
⑴取AC, AE的中点F、Q,分别连接 PB、PM. QD、QM,下列相等关系错误的是( )
A. MP = DQ = AE B. QM = BP= AC C. QM = BP=CE
⑵下列关于角的条件中,可以用来进一步判定△QDM≌△PMB的条件的是( )
A. ∠DEA = ∠BCA = ∠BAC B. ∠CPM = ∠CAE = ∠MQE
⑶综上,判定△QDM≌△PMB 的依据是( ),进而得到BM = DM.
SAS B.HL
2.如图,D是△ABC中AB边的中点,△BCE和△ACF都是等边三角形,M、N分别是CE、CF的中点,连接EF, Q是EF的中点, CP丄EF于点P,求证:DP = DQ.
取AC的中点G连接NG, DG, NQ, MP
①欲证DP = DQ,只需要证明( )
∠NQD = ∠MPD B.∠NDQ = ∠MDP C. △DNQ≌△DMP
②NQ = ___ , MP=_____.
③欲证△NDM为等边三角形,只需证明( )
A.∠DNM = 60° B. ND = NM C. ND = NM, ∠DNM = 60°
④证明△NGD≌△NCM,GD=_____, CM =_____,
∠GNC =______°,∠NGD + ∠4 = ______?, ∠4 + ∠5 = ______?
证明△NGD≌△NCM的判断依据是_______
20.构造直角三角形斜边中线答案
基础练:1.①C ②B ③A
证明:取AC、CE的中点P、Q,分别连接PB、PM、QD、QM
在Rt△ABC中,P是斜边AC的中点, ∴BP =,
在Rt△CDE中,Q是斜边CE的中点
∴DQ = CE, ∵Q、M分别是△AEC中边CE、AE的中点, ∴QM∥AC, QM = AC
∵P、M分别是△AEC中边AC、AE的中点, ∴MP//CE, MP =CE
∴ MP = DQ= CE, QM = BP = AC ,∵QM //AC, ∴∠MQE = ∠ACE
∵PM∥CE ,∴∠APM = ∠ACE, ∠APM = ∠ACE = ∠MQE, ∵∠APB = ∠DQE = 90°
∴∠APM + ∠APB = ∠MQE+∠DQE, ∴∠MPB =∠DQM, ∴△QDM≌△PMB(SAS),∴BM = DM
2.①C ②CE; CE; ③ C;④ BC; CE; 60;240; 240; SAS.
取AC的中点G,连接NG, DG
①证△NGD≌△NCM
先证明NG = NC及△GNC为等边三角形.
∵点N、 G分别是CF、AC的中点
∴GN = AF, ∵△ACF为等边三角形
∴AC = CF = AF ∴GN = NC = CG
∴△GNC为等边三角形
再证明 ∠NGD = ∠5
∠1 = ∠2 = ∠GNC = 60°
∵点D是AB的中点 , ∴ GD = CB, GD//CB ∴∠3 +∠4 = 180°
∴∠1 +∠ 3 + ∠4 = 240° ,∴∠NGD + ∠4 = 240°
∵△BCE为等边三角形, ∴∠6 = 60°, BC = EC ,∠4 + ∠5 + ∠2 + ∠6 = 360°
∴∠4 + ∠5 = 240°,∴∠NGD = ∠5
证明GD= CM
点M是CE的中点,∴CM = CE, ∵GD = CB, CB = CE,∴GD = CM
∴△NGD≌△NCM(SAS)
②证等边三角形
∴ND = NM, ∠7 = ∠8, △NDM为等腰三角形 ∵∠GNC = 60°,∠7 + ∠9 = 60°
∴∠DNM = ∠8 + ∠9 = 60°, ∴△NDM为等边三角形
再证△NQD≌△MPD
连接NQ, MP ∵△NDM为等边三角形 , ND = MD
①证NQ = MP
∵点N、Q分别是FE、FC的中点, ∴ NQ = CE, NQ//CE
∵点M是EC的中点,CP丄EF, ∴MP = CE ,NQ = MP
②证 ∠DNQ = ∠DMP
∵点N、M分别是FE、CE的中点 , ∴MN//EF, ∠10 = ∠ll, ∠12 = ∠13
∵NQ//CE, ∴∠ll = ∠14, ∵PM = CE = ME, ∴∠13 = ∠14 (等边对等角)
∴∠10 = ∠12, 又∵∠DNM = ∠DMN = 60°,∴∠10 = ∠12
∴∠DNQ =∠DMP, ∴△NQD≌△MPD(SAS), ∴DP= DQ。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
