苏科版七年级数学下册7.4认识三角形课件(共17张ppt)
文档属性
| 名称 | 苏科版七年级数学下册7.4认识三角形课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 16:01:58 | ||
图片预览




文档简介
(共17张PPT)
7.4 认识三角形
探索发现
日常生活中的三角形
试举出类似的实例,并与同学交流.
思考:
如何表示三角形?你知道哪些类型的三角形?
三角形介绍:
三角形是由3条不在同一条直线上的线段,首位依次相接组成的图形.
a
b
c
△ABC中∠A所对的边BC可以用a 表示.类似地,∠B所对的边AC、∠C所对的边AB也可以分别用b、C表示.
三角形分类:锐角三角形、直角三角形、钝角三角形、等腰三角形……
做一做
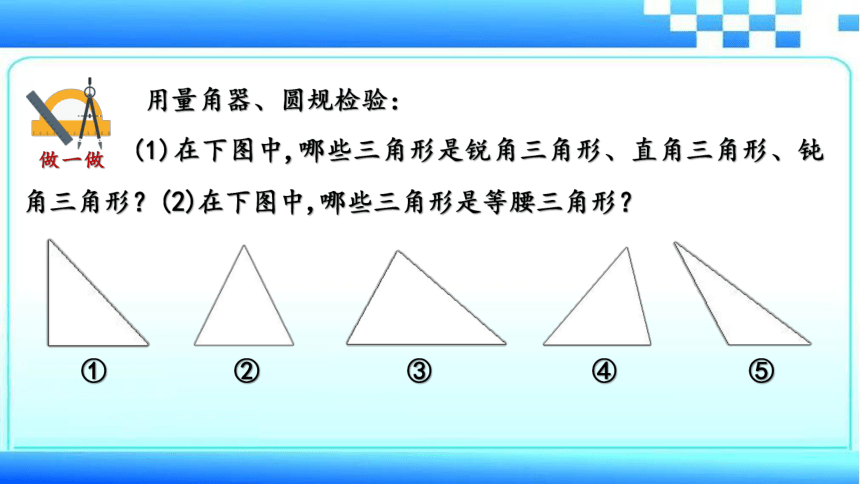
用量角器、圆规检验:
(1)在下图中,哪些三角形是锐角三角形、直角三角形、钝角三角形?(2)在下图中,哪些三角形是等腰三角形?
①
②
③
④
⑤
数学实验室
从长度分别为3cm、4cm、5cm、6cm和9cm的小木棒(如图)中任意取三根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
6cm
9cm
想一想
取3cm、5cm、9cm的能搭成吗?三边需要满足什么关系?
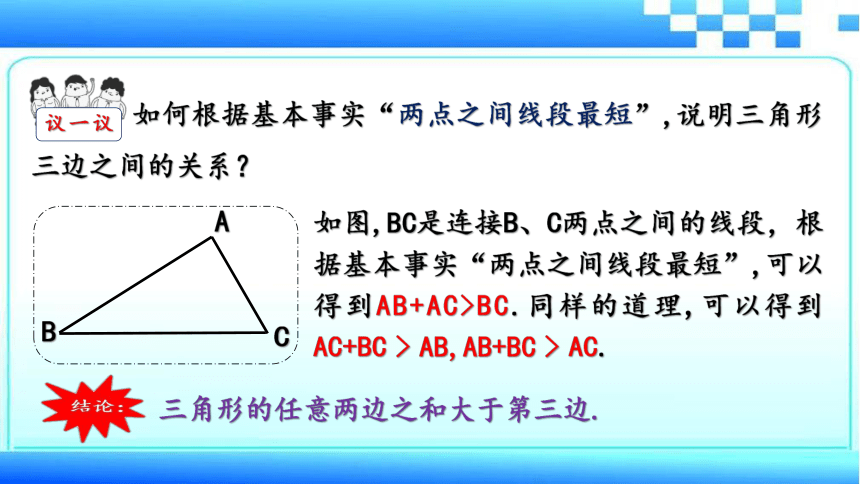
如何根据基本事实“两点之间线段最短”,说明三角形三边之间的关系?
A
B
C
如图,BC是连接B、C两点之间的线段,根据基本事实“两点之间线段最短”,可以得到AB+AC>BC.同样的道理,可以得到AC+BC > AB,AB+BC > AC.
三角形的任意两边之和大于第三边.
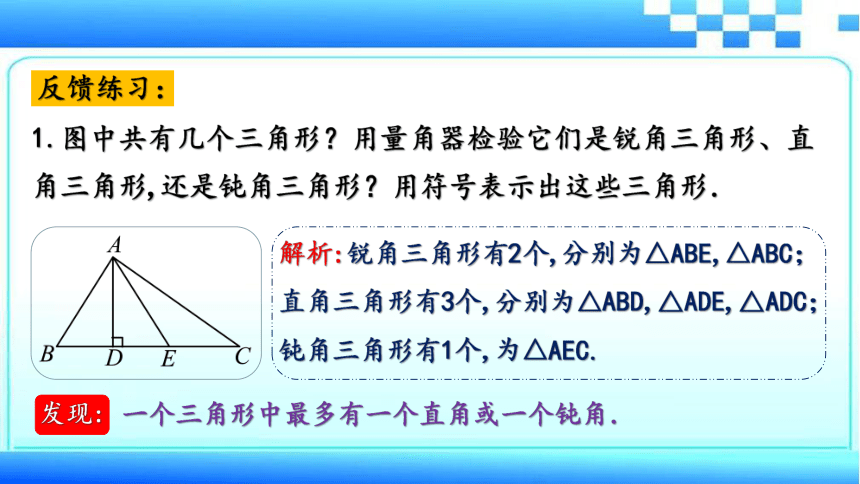
1.图中共有几个三角形?用量角器检验它们是锐角三角形、直角三角形,还是钝角三角形?用符号表示出这些三角形.
反馈练习:
解析:锐角三角形有2个,分别为△ABE,△ABC;
直角三角形有3个,分别为△ABD,△ADE,△ADC;
钝角三角形有1个,为△AEC.
发现:
一个三角形中最多有一个直角或一个钝角.
归纳总结:
数三角形个数的四种方法
(1)按照三角形形成的先后顺序去数;
(2)按照三角形的大小顺序去数;
(3)从图中的某一条线段开始沿着一定的方向去数;
(4)先固定一个顶点,再变换另两个顶点去数.
反馈练习:
2.以下列长度的三条线段为边,能构成三角形的是( )
A.6 cm,8 cm,10 cm;
B.3 cm,8 cm,11 cm;
C.3 cm,4 cm,10 cm;
D.三条线段的长度之比为5∶6∶13.
A
解析:在判断时一般检查较短的两边之和是否大于最长边.
如图,橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC移动到点C.在这个过程中,橡皮筋的位置不断变化,你认为其中有哪些位置是特殊的?请与同学交流.
A
B
C
1.橡皮筋的另一端落在BC的中点上.
2.橡皮筋平分∠BAC.
3.橡皮筋与BC所在的直线垂直.
如图,F是边BC的中点,我们把线段AF叫做△ABC的中线.
在三角形中,连接一个顶点与它对边中点的线段叫做三角形的中线.
三角形“三线”的介绍:
如图,线段AE平分∠BAC交BC于点E,我们把线段AE叫做△ABC的角平分线.
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形“三线”的介绍:
如图,线段AD垂直于BC,垂足为D,我们把线段AD叫做△ABC的高.
在三角形中,从一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.简称三角形的高.
三角形“三线”的介绍:
3.用折纸的方法折出一张三角形纸片的角平分线,能折出几条?你有什么发现?
三角形的3条角平分线都在三角形的内部,并且交于一点.
三角形的3条中线都在三角形的内部,并且交于一点.
反馈练习:
4.画出下图中的中线,分别能画出几条?你有什么发现?
反馈练习:
5.分别指出图中△ABC 的三条高.
BC边上的高是 ;
AB
AB边上的高是 ;
CB
AC边上的高是 .
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 .
BF
反馈练习:
6.一个等腰三角形的两边长分别为2.5和5,求这个三角形的周长.
(1)若2.5为腰长,则2.5+2.5=5,
出现了两边之和等于第三边,此时不能构成三角形;
(2)若5为腰长,则2.5+5=7.5>5,符合三角形的三边关系,
能构成三角形,
所以三角形的周长为2.5+5+5=12.5.
解析:由于不清楚腰长,则需要把所给出的边长进行分类讨论.
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
7.4 认识三角形
探索发现
日常生活中的三角形
试举出类似的实例,并与同学交流.
思考:
如何表示三角形?你知道哪些类型的三角形?
三角形介绍:
三角形是由3条不在同一条直线上的线段,首位依次相接组成的图形.
a
b
c
△ABC中∠A所对的边BC可以用a 表示.类似地,∠B所对的边AC、∠C所对的边AB也可以分别用b、C表示.
三角形分类:锐角三角形、直角三角形、钝角三角形、等腰三角形……
做一做
用量角器、圆规检验:
(1)在下图中,哪些三角形是锐角三角形、直角三角形、钝角三角形?(2)在下图中,哪些三角形是等腰三角形?
①
②
③
④
⑤
数学实验室
从长度分别为3cm、4cm、5cm、6cm和9cm的小木棒(如图)中任意取三根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
6cm
9cm
想一想
取3cm、5cm、9cm的能搭成吗?三边需要满足什么关系?
如何根据基本事实“两点之间线段最短”,说明三角形三边之间的关系?
A
B
C
如图,BC是连接B、C两点之间的线段,根据基本事实“两点之间线段最短”,可以得到AB+AC>BC.同样的道理,可以得到AC+BC > AB,AB+BC > AC.
三角形的任意两边之和大于第三边.
1.图中共有几个三角形?用量角器检验它们是锐角三角形、直角三角形,还是钝角三角形?用符号表示出这些三角形.
反馈练习:
解析:锐角三角形有2个,分别为△ABE,△ABC;
直角三角形有3个,分别为△ABD,△ADE,△ADC;
钝角三角形有1个,为△AEC.
发现:
一个三角形中最多有一个直角或一个钝角.
归纳总结:
数三角形个数的四种方法
(1)按照三角形形成的先后顺序去数;
(2)按照三角形的大小顺序去数;
(3)从图中的某一条线段开始沿着一定的方向去数;
(4)先固定一个顶点,再变换另两个顶点去数.
反馈练习:
2.以下列长度的三条线段为边,能构成三角形的是( )
A.6 cm,8 cm,10 cm;
B.3 cm,8 cm,11 cm;
C.3 cm,4 cm,10 cm;
D.三条线段的长度之比为5∶6∶13.
A
解析:在判断时一般检查较短的两边之和是否大于最长边.
如图,橡皮筋的一端固定在△ABC的顶点A上,另一端从点B出发沿BC移动到点C.在这个过程中,橡皮筋的位置不断变化,你认为其中有哪些位置是特殊的?请与同学交流.
A
B
C
1.橡皮筋的另一端落在BC的中点上.
2.橡皮筋平分∠BAC.
3.橡皮筋与BC所在的直线垂直.
如图,F是边BC的中点,我们把线段AF叫做△ABC的中线.
在三角形中,连接一个顶点与它对边中点的线段叫做三角形的中线.
三角形“三线”的介绍:
如图,线段AE平分∠BAC交BC于点E,我们把线段AE叫做△ABC的角平分线.
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
三角形“三线”的介绍:
如图,线段AD垂直于BC,垂足为D,我们把线段AD叫做△ABC的高.
在三角形中,从一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线.简称三角形的高.
三角形“三线”的介绍:
3.用折纸的方法折出一张三角形纸片的角平分线,能折出几条?你有什么发现?
三角形的3条角平分线都在三角形的内部,并且交于一点.
三角形的3条中线都在三角形的内部,并且交于一点.
反馈练习:
4.画出下图中的中线,分别能画出几条?你有什么发现?
反馈练习:
5.分别指出图中△ABC 的三条高.
BC边上的高是 ;
AB
AB边上的高是 ;
CB
AC边上的高是 .
BD
AB边上的高是 ;
CE
BC边上的高是 ;
AD
CA边上的高是 .
BF
反馈练习:
6.一个等腰三角形的两边长分别为2.5和5,求这个三角形的周长.
(1)若2.5为腰长,则2.5+2.5=5,
出现了两边之和等于第三边,此时不能构成三角形;
(2)若5为腰长,则2.5+5=7.5>5,符合三角形的三边关系,
能构成三角形,
所以三角形的周长为2.5+5+5=12.5.
解析:由于不清楚腰长,则需要把所给出的边长进行分类讨论.
作业:完成课时作业本相应习题.
要求:字迹工整,表述科学.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
