江苏省沭阳县2020届高三下学期联考数学试题 扫描版含答案
文档属性
| 名称 | 江苏省沭阳县2020届高三下学期联考数学试题 扫描版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 13:44:36 | ||
图片预览


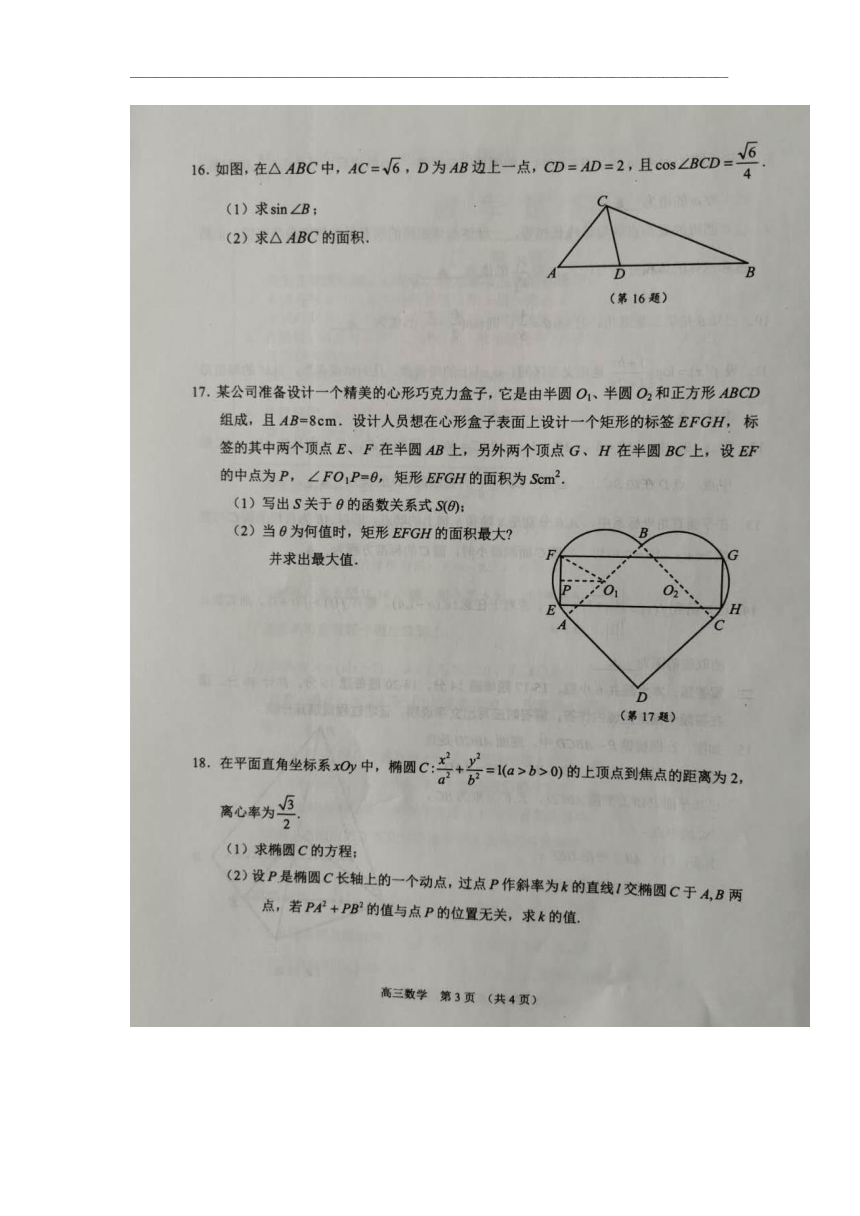


文档简介
2019~2020学年度第二学期高三年级5月联考
数学参考答案
参考公式:1.方差公式:;
2.球的体积公式:,是球的半径.
一、填空题:本大题共14小题,每小题5分,共计70分.不需写出解题过程,请把答案直接填写在答题卡相应位置上.
1.
2.
3. 6
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
二、解答题:本大题共6小题,15-17题每题14分,18-20题每题16分,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.
证明:(1)因为,,为的中点.,
所以,所以四边形是平行四边形,
所以 …………3分
又因为平面,平面
所以平面. …………6分
(2)因为平面平面
平面平面
,平面
所以平面. …………8分
因为平面.
所以 …………10分
因为分别为的中点,
所以, 所以
因为,
所以 …………12分
因为平面,平面,
所以平面. …………14分
16.
解:(1)在中,由余弦定理得
…………2分
所以 …………4分
因为,是三角形的内角,
所以 …………6分
所以
…………8分
(2)在中,由正弦定理得 …………10分
…………12分
所以. …………14分
注:其它方法酌情给分!
17.
解:(1)由题意知, …………2分
,
, …………4分
则,
即,. …………6分
(2)
…………8分
因为,所以
所以, …………10分
故当时,恒成立,
所以在上单调递增, …………12分
故当时,.
答:当θ为时,矩形EFGH的面积最大,最大值为. …………14分
18.
解:(1)由题设可知,所以,故,因此
所以椭圆的方程为 …………3分
(2)设
①若,则直线的方程为
联立直线与椭圆的方程,即,
消去,化简得, …………5分
所以
又,…………7分
点到直线的距离,
所以
当且仅当,即时,取得最大值1. …………9分
②设直线的方程为.
将直线与椭圆的方程联立,即
消去,化简得 …………11分
所以.
所以-
=, …………14分
因为的值与点的位置无关,即上式取值与无关,
故有,解得. …………16分
19.
解:(1)当时,,则,
在处的切点为,切线斜率为,
所以函数在处的切线方程为. …………3分
(2)因为.
所以的定义域为; ,
又因为函数在定义域上为单递增函数,
所以在时恒成立,
即在时恒成立, …………6分
设,
则,
当时,,则在上为减函数,
当时,,则在上为增函数, …………8分
在时恒成立,
所以. …………9分
(3)因为,
所以,则不可能对恒成立,
即在定义域上不可能始终都为减函数, …………10分
由(2)知函数为增函数,
所以若函数在定义域上不是单调函数
又因为,所以是函数一个零点,
令,得
设,则与有相同的零点,
令,得,
因为,所以,
所以有两个不相等实数解,
因为,所以不妨设, …………12分
当时,,在为增函数
当时,,在为减函数
当时,,在为增函数
则 ………14分
又因为时,,
,,
又因为在图象不间断,所以在有唯一一个零点
又因为在图象不间断,所以在有唯一一个零点
又因为是函数一个零点,
综上函数必有三个不同零点. …………16分
20.
解:(1)因为an=,所以Sn=×=1-()n, ………………2分
所以an+1-Sn=()n+1-1+()n=()n-1≤×-1=-<0,
所以an+1<Sn,即{an}∈M. ………………4分
(2)设{an}的公差为d,因为{an+n}∈M,
所以an+1+n+1≤(a1+1)+(a2+2)+…+(an+n) (*)
特别的当n=1时,a2+2≤a1+1,即d≤-1,
由(*)得a1+nd+n+1≤na1+d+, ………………6分
整理得n2+(a1-d-)n-a1-1≥0,
因为上述不等式对一切n∈N*恒成立,所以必有≥0,解得d≥-1,
又d≤-1,所以d=-1, ………………8分
于是(a1+1)n-a1-1≥0,即(a1+1)(n-1)≥0,所以a1+1≥0,
即a1≥-1, ………………10分
(3)由an+1≤Sn得Sn+1-Sn≤Sn,所以Sn+1≤2Sn,即≤2,
所以=××…×≤2n,从而有Sn+1≤S1×2n=a1×2n,
又an+1≤Sn,所以an+2≤Sn+1≤a1×2n,即an≤a1×2n-2(n≥3),
又a2≤S1=a1×22-2,a1<a1×21-2,所以有an≤a1×2n-2(n∈N*),
所以≥×2n, ………………12分
假设数列{}中存在无穷多项依次成等差数列,
不妨设该等差数列的第n项为dn+b(b为常数),
则存在m∈N,m≥n,使得dn+b=≥×2m≥×2n,即da1n+ba1≥2n+2,
设f (n)=,n∈N*,n≥3, 则f (n+1)-f (n)=-=<0,
即f (n+1)<f (n)≤f (3)=<1, ………………14分
于是当n≥3时,2n+2>n2,从而有:当n≥3时da1n+ba1>n2,即n2-da1n-ba1<0,
于是当n≥3时,关于n的不等式n2-da1n-ba1<0有无穷多个解,显然不成立,
因此数列{}中是不存在无穷多项依次成等差数列. ………………16分
附加题
21.【选做题】本题包括A、B、C三小题,请选定其中两小题,并在相应的答题区域内作答,若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.
解:(1)由条件,得. …………4分
(2)设变换后新曲线上任一点,变换前对应点,则
,即 …………6分
,代入得:
所以曲线在的作用下的新曲线的方程为 …………10分
B.[选修4-4:坐标系与参数方程]
解:由消去参数得圆的普通方程为,圆心坐标为, ………5分
过圆心且与极轴垂直的直线的直角坐标方程为,
化为极坐标方程为 ……10分
C.[选修4-5:不等式选讲]
解: ………………………………5分
………………8分
当且仅当即时取最大值 …10分
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.
22.
解:如图,以点为原点,分别为轴建立
空间直角坐标系,则.………… 1分
(1)所以,
设平面一个法向量为
由得,取 ………… 4分
设直线与平面所成角为,
所以
所以直线与平面所成角的正弦值为. ………… 6分
(2)由(1)知平面一个法向量为
取平面一个法向量 ………… 7分
………… 9分
由图知二面角的余弦值为 ………… 10分
23.
解:由题设.设,则,且
.
记过两点的直线为,则的方程为.
(1)由于在线段上,故.
记的斜率为,的斜率为,则
.
所以. ………… 4分
(2)设与轴的交点为,
则.
由题设可得,所以(舍去),. ………… 6分
设满足条件的的中点为.
当与轴不垂直时,由可得,而,所以. ………… 9分
当与轴垂直时,与重合.
所以,所求轨迹方程为. ………… 10分
同课章节目录
