滕州市级索中学北师大版8年级下册数学5.4分式方程测试(含答案)
文档属性
| 名称 | 滕州市级索中学北师大版8年级下册数学5.4分式方程测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 52.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 08:28:02 | ||
图片预览
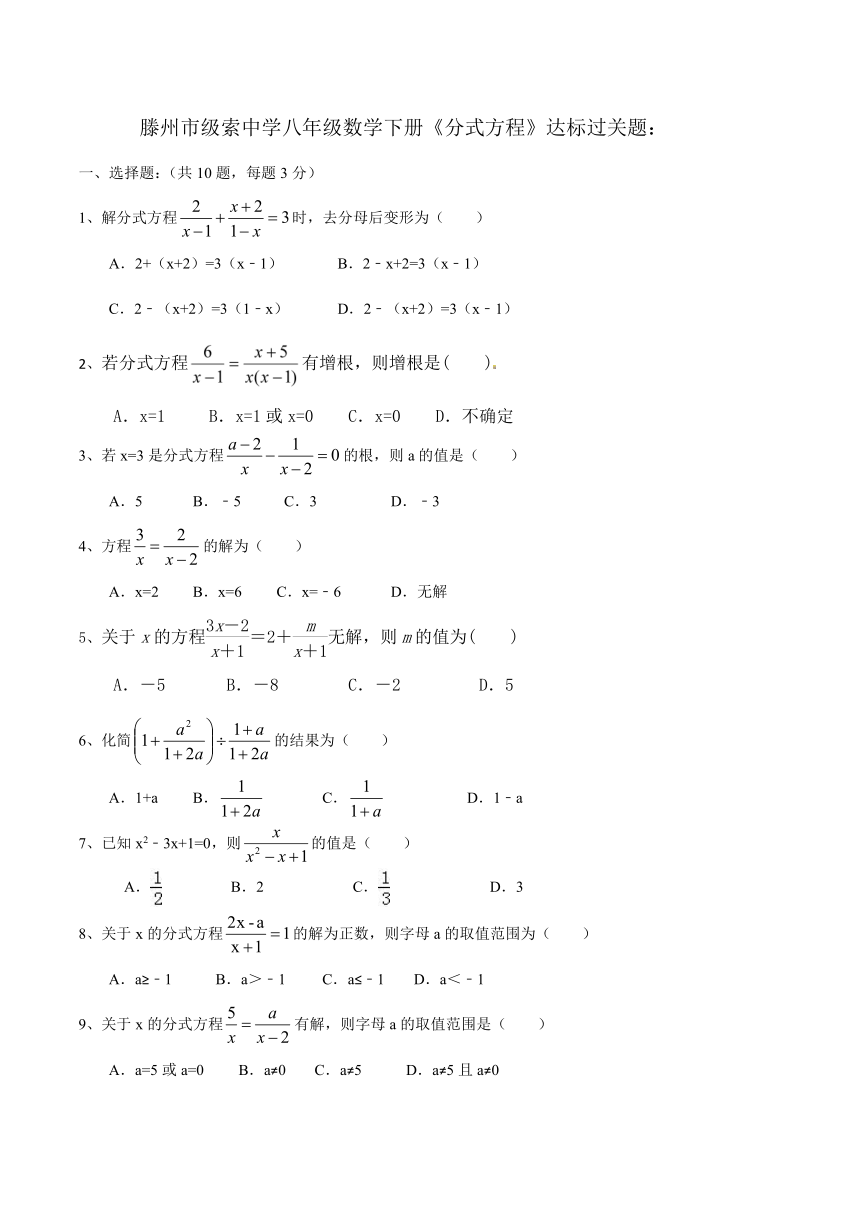

文档简介
滕州市级索中学八年级数学下册《分式方程》达标过关题:
选择题:(共10题,每题3分)
1、解分式方程时,去分母后变形为( )
A.2+(x+2)=3(x﹣1) B.2﹣x+2=3(x﹣1)
C.2﹣(x+2)=3(1﹣x) D.2﹣(x+2)=3(x﹣1)
2、若分式方程有增根,则增根是( )
A.x=1 B.x=1或x=0 C.x=0 D.不确定
3、若x=3是分式方程的根,则a的值是( )
A.5 B.﹣5 C.3 D.﹣3
4、方程的解为( )
A.x=2 B.x=6 C.x=﹣6 D.无解
5、关于x的方程=2+无解,则m的值为( )
A.-5 B.-8 C.-2 D.5
6、化简的结果为( )
A.1+a B. C. D.1﹣a
7、已知x2﹣3x+1=0,则的值是( )
A. B.2 C. D.3
8、关于x的分式方程的解为正数,则字母a的取值范围为( )
A.a≥﹣1 B.a>﹣1 C.a≤﹣1 D.a<﹣1
9、关于x的分式方程有解,则字母a的取值范围是( )
A.a=5或a=0 B.a≠0 C.a≠5 D.a≠5且a≠0
10、为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元.若设甲型机器人每台x万元,根据题意,所列方程正确的是( )
A.= B.=
C.+=140 D.﹣140=
二、填空题:(每空3分)
1、解分式方程的基本思想是把分式方程化为 ,最后要注意 .
2、分式方程去分母时,两边都乘以 .
3、当x= 时,的值相等.
4、若,则 .
5、若关于x的分式方程-2=有增根,则增根为________,m=________.
6、方程的解为_______
7、若分式方程有增根,则实数a的取值是_______.
三:解方程:(共24分,每题6分)
(3):+=—1 (4):﹣1=.
列方程解应用题:(共14分,1题8分;2题11分)
(1)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗?
(2)节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
参考答案:
一、选择题:1-10、DBABA AABCA
二:填空题:1、整式方程,检验 2、(x-1)(x+1) 3、3 4、-3
3 3 6、 7、4或8
三、解方程:(1)x=2 (2)无实数解
(3)经检验x=2是增根,分式方程无实数解.
(4):方程两边都乘以(x+1)(x﹣1)去分母得,
x(x+1)﹣(x2﹣1)=3,
即x2+x﹣x2+1=3,
解得x=2
检验:当x=2时,(x+1)(x﹣1)=(2+1)(2﹣1)=3≠0,
∴x=2是原方程的解,
故原分式方程的解是x=2.
四、列方程解应用题:
(1)解:设乙每小时做x 面彩旗,则甲每小时做(x+5)面彩旗。
根据题意,得
解这个方程,得x=25.经检验,x=25 是所列方程的解. ∴x+5=30
答:甲每小时做30 面彩旗,乙每小时做25 面彩
(2)解:(1)设汽车行驶中每千米用电费用是x元,则每千米用油费用为(x+0.5)元,
可得:,
解得:x=0.3,
经检验x=0.3是原方程的解,
∴汽车行驶中每千米用电费用是0.3元,甲、乙两地的距离是30÷0.3=100千米;
(2)汽车行驶中每千米用油费用为0.3+0.5=0.8元,
设汽车用电行驶ykm,
可得:0.3y+0.8(100﹣y)≤50,
解得:y≥60,所以至少需要用电行驶60千米.
选择题:(共10题,每题3分)
1、解分式方程时,去分母后变形为( )
A.2+(x+2)=3(x﹣1) B.2﹣x+2=3(x﹣1)
C.2﹣(x+2)=3(1﹣x) D.2﹣(x+2)=3(x﹣1)
2、若分式方程有增根,则增根是( )
A.x=1 B.x=1或x=0 C.x=0 D.不确定
3、若x=3是分式方程的根,则a的值是( )
A.5 B.﹣5 C.3 D.﹣3
4、方程的解为( )
A.x=2 B.x=6 C.x=﹣6 D.无解
5、关于x的方程=2+无解,则m的值为( )
A.-5 B.-8 C.-2 D.5
6、化简的结果为( )
A.1+a B. C. D.1﹣a
7、已知x2﹣3x+1=0,则的值是( )
A. B.2 C. D.3
8、关于x的分式方程的解为正数,则字母a的取值范围为( )
A.a≥﹣1 B.a>﹣1 C.a≤﹣1 D.a<﹣1
9、关于x的分式方程有解,则字母a的取值范围是( )
A.a=5或a=0 B.a≠0 C.a≠5 D.a≠5且a≠0
10、为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用360万元购买甲型机器人和用480万元购买乙型机器人的台数相同,两种型号机器人的单价和为140万元.若设甲型机器人每台x万元,根据题意,所列方程正确的是( )
A.= B.=
C.+=140 D.﹣140=
二、填空题:(每空3分)
1、解分式方程的基本思想是把分式方程化为 ,最后要注意 .
2、分式方程去分母时,两边都乘以 .
3、当x= 时,的值相等.
4、若,则 .
5、若关于x的分式方程-2=有增根,则增根为________,m=________.
6、方程的解为_______
7、若分式方程有增根,则实数a的取值是_______.
三:解方程:(共24分,每题6分)
(3):+=—1 (4):﹣1=.
列方程解应用题:(共14分,1题8分;2题11分)
(1)甲、乙两位同学同时为校文化艺术节制作彩旗.已知甲每小时比乙多做5面彩旗,甲做60面彩旗与乙做50面彩旗所用时间相等,问甲、乙每小时各做多少面彩旗?
(2)节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
参考答案:
一、选择题:1-10、DBABA AABCA
二:填空题:1、整式方程,检验 2、(x-1)(x+1) 3、3 4、-3
3 3 6、 7、4或8
三、解方程:(1)x=2 (2)无实数解
(3)经检验x=2是增根,分式方程无实数解.
(4):方程两边都乘以(x+1)(x﹣1)去分母得,
x(x+1)﹣(x2﹣1)=3,
即x2+x﹣x2+1=3,
解得x=2
检验:当x=2时,(x+1)(x﹣1)=(2+1)(2﹣1)=3≠0,
∴x=2是原方程的解,
故原分式方程的解是x=2.
四、列方程解应用题:
(1)解:设乙每小时做x 面彩旗,则甲每小时做(x+5)面彩旗。
根据题意,得
解这个方程,得x=25.经检验,x=25 是所列方程的解. ∴x+5=30
答:甲每小时做30 面彩旗,乙每小时做25 面彩
(2)解:(1)设汽车行驶中每千米用电费用是x元,则每千米用油费用为(x+0.5)元,
可得:,
解得:x=0.3,
经检验x=0.3是原方程的解,
∴汽车行驶中每千米用电费用是0.3元,甲、乙两地的距离是30÷0.3=100千米;
(2)汽车行驶中每千米用油费用为0.3+0.5=0.8元,
设汽车用电行驶ykm,
可得:0.3y+0.8(100﹣y)≤50,
解得:y≥60,所以至少需要用电行驶60千米.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
