人教版八年级下册数学易错题专项训练 19.3 课题学习 选择方案测试题(含解析)
文档属性
| 名称 | 人教版八年级下册数学易错题专项训练 19.3 课题学习 选择方案测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:58:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级下册易错题专题
19.3 选择方案
一.选择题(共5小题)
1.小兰和小琳约好在公共汽车站一起乘车去博物馆,小兰从家出发步行到车站,等小琳到了以后两人一起乘公共汽车到博物馆.图中的折线表示小兰距离博物馆的路程y(km)与所用时间x(min)之间的函数关系,下列说法错误的是( )
A.小兰从家到公共汽车站步行了1km
B.小兰在公共汽车站等汽车用了15min
C.公共汽车的平均速度为30kmh
D.小兰和小琳乘公共汽车用了55min
2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=或t=,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
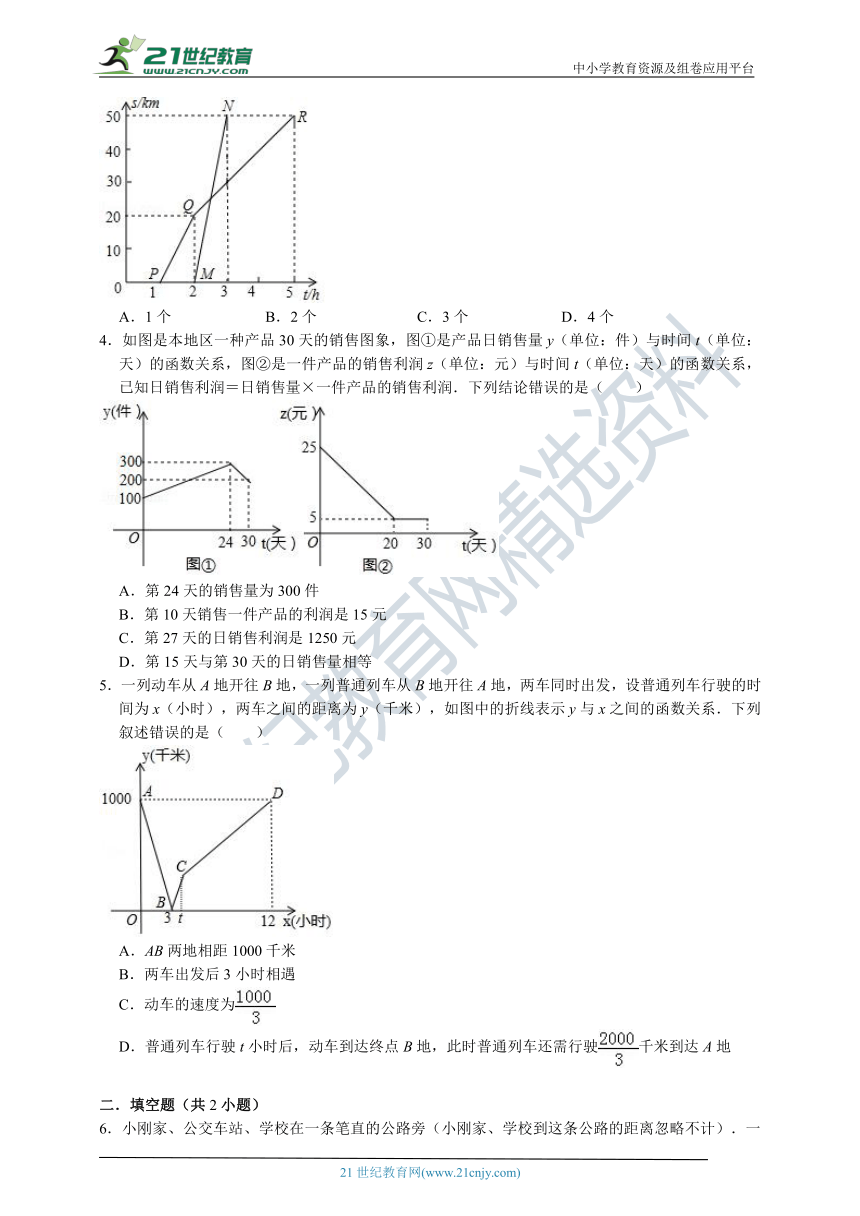
3.如图A、B两地相距50km.甲于某日下午1点骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地.图中折线PQR和线段MN分别表示甲和乙行驶的路程s与该日下午时间t之间的关系.下列说法正确的有( )
①甲、乙两人同时到达目的地;
②乙出发后30分钟后追上甲;
③甲的平均速度是10km/h,乙的速度是50km/h;
④甲、乙相遇是距出发地25km.
A.1个 B.2个 C.3个 D.4个
4.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
A.第24天的销售量为300件
B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元
D.第15天与第30天的日销售量相等
5.一列动车从A地开往B地,一列普通列车从B地开往A地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系.下列叙述错误的是( )
A.AB两地相距1000千米
B.两车出发后3小时相遇
C.动车的速度为
D.普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶千米到达A地
二.填空题(共2小题)
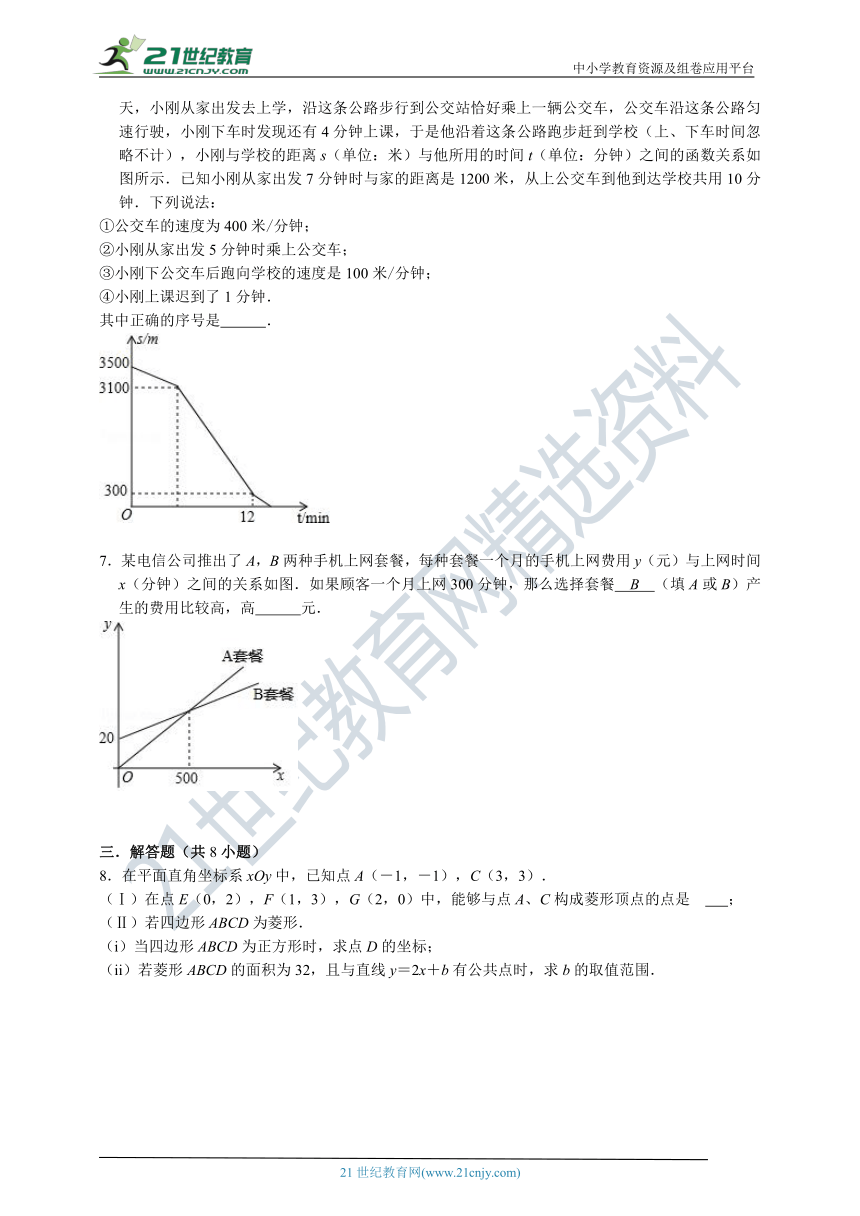
6.小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计).一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校共用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的序号是 .
7.某电信公司推出了A,B两种手机上网套餐,每种套餐一个月的手机上网费用y(元)与上网时间x(分钟)之间的关系如图.如果顾客一个月上网300分钟,那么选择套餐 B (填A或B)产生的费用比较高,高 元.
三.解答题(共8小题)
8.在平面直角坐标系xOy中,已知点A(-1,-1),C(3,3).
(Ⅰ)在点E(0,2),F(1,3),G(2,0)中,能够与点A、C构成菱形顶点的点是 ;
(Ⅱ)若四边形ABCD为菱形.
(i)当四边形ABCD为正方形时,求点D的坐标;
(ii)若菱形ABCD的面积为32,且与直线y=2x+b有公共点时,求b的取值范围.
9.如图,在平面直角坐标系中,直线y=-x-1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(-1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
(1)是否存在t,使得以P为圆心,为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
10.如图,直线L1:y=x+1与直线L2:y=-x+5相交于点C直线L1与x轴相交于点A,直线L2与x轴相交于点B.
(1)求三角形ABC的面积;
(2)若经过点C的一条直线交x轴于D,直线CD把三角形ABC分成两个三角形,且这两个三角形面积的比为1:2,请直接写出点D的坐标;
(3)假设G是直线y=x+1上的点,在坐标平面上是否存在一点Q,使以A,B,Q,G为顶点的四边形是正方形,若存在求出点Q的坐标,若不存在请说明理由.
11.如图,直线y=-x+3与x轴相交于点B,与y轴相交于点A,点E为线段AB中点,∠ABO的平分线BD与y轴相较于点D,点A、C关于点O对称.
(1)求线段DE的长;
(2)一个动点P从点D出发,沿适当的路径运动到直线BC上的点F,再沿射线CB方向移动2个单位到点G,最后从点G沿适当的路径运动到点E处,当P的运动路径最短时,求此时点G的坐标;
(3)将△ADE绕点A顺时针方向旋转,旋转角度α(0<α≤180°),在旋转过程中DE所在的直线分别与直线BC、直线AC相交于点M、点N,是否存在某一时刻使△CMN为等腰三角形,若存在,请求出CM的长,若不存在,请说明理由.
12.某文具店四月份购进甲、乙两种文具共80件,分别用去400元、1200元,甲种文具每件的进价是乙种文具的.请解答下列问题:
(1)求甲、乙两种文具每件的进价;
(2)五月份文具店决定再次购进甲、乙两种文具共80件,进价不变,甲、乙文具每件售价分别是15元、40元.若80件文具全部售出,求销售甲乙文具获利y(元)与购进甲种文具x(件)之间的函数解析式;
(3)在(2)的条件下,销售前文具店决定从这80件文具中拿出一部分,赠送给某校在“牡丹江首届汉字听写电视大赛”获一、二等奖的6名同学,作为奖品,其余文具全部售出.已知一等奖每人1件甲种文具,3件乙种文具;二等奖每人4件甲种文具,1件乙种文具,这些奖品总进价超过450元,文具店购进的80件文具仅获利30元.请直接写出文具店购进甲、乙两种文具的方案.
13.为了推进“河长制”保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台,每台设备价格及月处理污水量如下表所示:
污水处理设备 A型 B型
价格(万元/台) 15 12
月处理污水量(吨/台) 220 180
(1)设购买A型设备x台,每月处理污水总最为W吨,试写出W与x的函数关系式;
(2)由于受受资金限制,指挥部用于购买污水处理设备的资金不超过135万元,问购买A型设备多少台才能使每月处理污水量最多?
14.某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,甲服装店租用2件和在乙服装店租用3件共需280元,在甲服装店租用4件和在乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,且超出5件的部分可按原价的六折进行优惠;设需要租用x件服装,选择甲店则需要y1元,选择乙店则需要y2元,请分别求出y1,y关于x的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
15.某玩具厂分别安排甲乙两个车间加工1000个同一型号的奥运会吉祥物,每名工人每天加工吉祥物的个数相等且保持不变,由于生产需要,其中一个车间推迟两天开始加工,刚开始加工时,甲车间有10名工人,乙车间有12名工人,图中线段OB和折线ACB分别表示两个车间的加工情况.依据图中提供的信息,完成下列各题:
(1)线段OB反映的是 车间的加工情况;
(2)开始加工后,甲车间加工多少天后,两车间加工吉祥物数相同?
(3)根据折线段反映的加工情况,请你提出一个问题,并给出解答.
参考答案
一.选择题
1.解:A、小兰从家到公共汽车站步行了1km,正确;
B、小兰在公共汽车站等汽车用了15min,正确;
C、公共汽车的平均速度为km/h,正确;
D、小兰和小琳乘公共汽车用了55-25=30min,错误;
故选:D.
2.解:由图象可知A、B两城市之间的距离为300km,故①正确;
甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②错误;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
把y=150代入y甲=60t,可得:t=2.5,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(2.5,150)代入可得,解得,
∴y乙=100t-100,
令y甲=y乙可得:60t=100t-100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;
令|y甲-y乙|=40,可得|60t-100t+100|=40,即|100-40t|=40,
当100-40t=40时,可解得t=,
当100-40t=-40时,可解得t=,
又当t=时,y甲=40,此时乙还没出发,
当t=时,乙到达B城,y甲=260;
综上可知当t的值为或或或t=时,两车相距40千米,故④不正确;
故选:A.
3.解:①乙比甲早到B城,早了5-3=2个小时;所以甲、乙两人同时到达目的地是错误的;
②由图可知:M(2,0),N(3,50),Q(2,20),R(5,50)
设直线QR的函数表达式为y1=k1x+b1,直线MN的函数表达式为y2=k2x+b2,
将各点坐标代入对应的表达式,得:
,解得:,
,
解得:,
∴y1=10x,y2=50x-100,
联立两式可得直线QR、MN的交点的坐标为O(2.5,25)
所以乙出发半小时后追上甲,
故乙出发后30分钟后追上甲是正确的;
③乙的速度为=50千米/时,甲的平均速度为=12.5千米/时,故甲的平均速度是10km/h,乙的速度是50km/h,是错误的;
④因为乙出发半小时后追上甲,所以甲、乙相遇是距出发地25km,是正确的;
故选:B.
4.解:A、根据图①可得第24天的销售量为300件,故正确;
B、设当0≤t≤20,一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系为z=kx+b,
把(0,25),(20,5)代入得:,
解得:,
∴z=-x+25,
当x=10时,y=-10+25=15,
故正确;
C、当24≤t≤30时,设产品日销售量y(单位:件)与时间t(单位;天)的函数关系为y=k1t+b1,
把(30,200),(24,300)代入得:,
解得:,
∴y=-t+700,
当t=27时,y=250,
∴第27天的日销售利润为;250×5=1250(元),故C正确;
D、当0<t<24时,可得y=t+100,t=15时,y≠200,故D错误,
故选:D.
5.解:由图可得,
AB两地相距1000千米,故选项A正确,
两车出发3小时相遇,故选项B正确,
动车的速度为:1000÷3-1000÷12=250千米/时,故选项C错误,
普通列车行驶t小时后,动车到达终点B地,此时普通列车还需行驶×(12-)=千米到达A地,故选项D正确,
故选:C.
二.填空题
6.解:∵小刚从家出发7分钟时与家的距离是1200米,即小刚从家出发7分钟时距离学校3500-1200=2300m,
∴公交车的速度为:=400米/分钟,故①正确;
由①知公交车速度为400米/分钟,
∴公交车行驶的时间为=7分钟,
∴小刚从家出发乘上公交车是在第12-7=5分钟时,故②正确;
∵从上公交车到他到达学校共用10分钟,
∴小刚下公交车后跑向学校的速度是=100米/分钟,故③正确;
∵小刚从下车至到达学校所用时间为5+10-12=3分钟,
而小刚下车时发现还有4分钟上课,
∴小刚下车较上课提前1分钟,故④错误;
故答案为:①②③
7.解:设yA=kAx,yB=kBx+20,
当x=500时,yA=yB,即500kA=500kB+20,
∴kB-kA=-,
当x=300时,yB-yA=300kB+20-300kA=300(kB-kA)+20=8,
∴如果一个月上网300分钟,那么方式B产生的费用比方式A高8元,
故答案为:B;8.
三.解答题
8.解:(Ⅰ)如图1中,四边形AECG是菱形,
故答案为E、G.
(Ⅱ)(i)如图2中,
∵A(-1,-1),C(3,3),四边形ABCD是正方形,
∴D(3,-1)或(-1,3);
(ii)如图3中,
∵四边形ABCD是菱形,面积为32,AC=4,
∴?AC?BD=32,
∴BD=8,
∴B(5,-3),D(-3,5)或B(-3,5),D(5,-3),
当直线y=2x+b经过(5,-3)时,-3=10+b,b=-13,
当直线y=2x+b经过(-3,5)时,6=-6+b,b=12,
∴当-13≤b≤12时,直线y=2x+b与菱形ABCD有公共点.
9.解:(1)假设存在点P.作PH⊥AB,PM⊥x轴交AB于Q.
∵PQ∥y轴,
∴∠OBA=∠PQH,
∵∠AOB=∠PHQ=Rt∠,
∴△PHQ∽△AOB,
∴=,
∵A(-1,2)或(-3,3),PH=,
∴AO=2,AB=,
∴PQ=,
①当点P在CD上时,t+1+=,解得t=1,
②当点P在DE上时,3-[-(1-t)-1]=,解得t=4,此时点P与E重合.
综上所述,满足条件的t的值为1或4.
(2)由题意平移后的直线A′B′的解析式为y=-x-1+,
作PH⊥A′B′,PM⊥x轴交A′B′于Q.
当PH=时,同法可得PQ=,
①当点P在CD上时,1+t-(-1+)=,解得t=,
②当点P在DE上时,3-[-(1-t)-1+]=,解得t=,
③当点P在EF上时,-1+-(6-t+1)=,解得t=,
综上所述,满足条件的t的值为或或.
10.解:(1)在y=x+1中,
当y=0时,则x=-1
∴A(-1,0)
在y=-x+5中
当y=0时,则x=5
B(5,0)
∴AB=OA+OB=6,
由
解得,
∴C(2,3)
∴作CE⊥x轴于E.
∴E(2,0)
∴CE=3
∴S△ABC=?AB?CE
=×6×3=9,
(2)由题意A(-1,0),B(5,0),AD=2BD或BD=2AD,
可得D(1,0)或D(3,0).
(3)设y=x+1交y轴于F,则F(0,1).
∴OF=OA
∴∠OAF=45°
同理∠ABC=45°
∴∠ACB=90°
∴CA=CB,
在L1上取点G(G异于A),且CG=CA,
在L2上取点Q(Q异于B),且CQ=CB
∴CG=CA=CQ=CB,
又∵AG⊥BQ,
∴四边形ABGQ为正方形,
又∵A(-1,0)
AB=AQ=6
∴Q(-1,6).
当G与C重合时,
以AB为对称轴作G的对称点Q,于是四边形AQBG为正方形.
又∵G(2,3),
∴Q(2,-3)
综合上述:Q(-1,6)或Q(2,-3).
11.解:(1)∵直线y=-x+3与x轴相交于点B,与y轴相交于点A,
∴A(0,3),B(,0),
∴OA=3,OB=,
∴tan∠ABO==,
∴∠ABO=60°,
∵BD平分∠ABO,
∴∠DBO=30°,
∴OD=OB?tan30°=1,DB=2OD=2,
∴AD=DB=2,
∴AE=EB,
∴DE⊥AB,∵DO⊥OB,DB平分∠ABO,
∴DE=DO=1.
(2)过点E作EE′∥BC,点E′在x轴下方且EE′=2,作点D关于直线BC的对称点D′,连接E′D′交BC于F,在射线CB上取FG=2.此时D→F→G→E的路径最短.
∵E′(-,-),D′(2,-1),
∴直线D′E′的解析式为y=-x-,直线BC的解析式为y=x-3,
由,解得,
∴F(,-).
把点F向上平移3个单位,向右平移个单位得到点G,
∴G(,).
(3)以点A为圆心,以AE为半径作⊙A,则DE为⊙A的切线.
①如图1中,当CM=CN时,在AE上取一点P,使得AP=PN.设EN=x.
∵CM=CN,∠MCN=30°,
∴∠CNM=∠CMN=75°,
∴∠ANE=∠CNM=75°,
∴∠EAN=15°,
∴∠PAN=∠ANP=15°,
∴∠EPN=30°,
∴PN=AP=2x,PE=x,
∴2x+x=,
∴x=2-3,
∴AN==3-,
∴CM=CN=6-(3-)=6+-3.
②如图2中,当MN=MC时,作BP⊥MN于P,则四边形ADPB是矩形,PB=AE=,
在Rt△PBM中,∠PBM=30°,
∴BM=2,
∴CM=BC-BM=2-2.
③如图3中,当NC=MN时,D与N重合,作DP⊥BC于P.
∵CD=6+2=8,∠DCP=30°,
∴PC=PM=4,
∴CM=8
综上所述,满足条件的CM的值为6+-3或2-2或8.
12.解:(1)设甲种商品每件的进价是x元,则乙种商品每件的进价为3x元,
依题意可得:,
解得:x=10,
经检验:x=10为原分式方程的解,且符合题意,
则3x=3×10=30,
答:甲、乙两种商品的进价分别为每件10元、30元;
(2)设:购进甲种文具x件,则购进乙文具为80-x件,由题意得:
y=(15-10)x+(40-30)(80-x)=-5x+800,
答:销售甲乙文具获利y(元)与购进甲种文具x(件)之间的函数解析式y-5x+800.
(3)设:购进甲种文具x件(购进乙文具为80-x件)、有a人获得一等奖(6-a人获得二等奖),由题意得:
①6名同学奖品的总价格:一等奖,甲为a元、乙为3a元,二等奖,甲4(6-a),乙6-a,
则:a+3a+4(6-a)+6-a≤450,解得:a≥1,即1≤a<6,
②发完奖品后,甲剩下文具x-(24-3a)=3a+x-24,甲剩下文具80-x-(6+2a)=74-x-2a,
由题意得:文具店购进的80件文具获利=发完奖品后两种文具获利-6名同学奖品的总进价,
即:30=(15-10)?(3a+x-24 )+(74-x-2a)(40-30)-(24-3a)?10+(6+2a)?30
解得:x=34-7a,由于1≤a<6,且a为正整数,
x=27,20,13,6.
乙文具:80-x=43,60,67,74.
答:购进甲、乙两种文具的方案有4种,甲乙分别为:27、43;20、60;13、67;6、74.
13.解:(1)购买A型设备x台,每月处理污水总最为W吨,
则W与x的函数关系式:W=220x+180(10-x)=40x+1800.
(2)设购买A型号a台,B型号(10-a)台,
由题意得,15a+12(10-a)≤135,
解得:a≤5,
因为W与a的函数关系式:W=220a+180(10-a)=40a+1800.
因为k=40>0,
所以当a=5时,才能使每月处理污水量最多.
14.解:(1)设甲店每件租金x元,乙店每件租金y元,由题可得:,
解得,
答:两个服装店提供的单价分别是50元.60元;
(2)根据题意可得:y1=40x,
y2=
(3)由40x=36x+120得x=30
答:当x=30时,两店相同.
15.解:(1)线段OB反映的是 甲车间的加工情况,
故答案为:甲;
(2)直线OB解析式:y=50x
A(2,0)、C(18,960),设直线AC解析式为:y=kx+b则,
解得:k=60,b=-120
直线AC解析式:y=60x-120
联立:,
解得:.
答:甲车间加工12天后,两车间加工的吉祥物数相同.
(3)问题:乙车间完成生产任务时需多少天,与甲同时完成生产任务,
设BC的函数解析式为:y=kx+b,B(20,1000)C(18,960)
,
解得:
∴y=20x+600,当y=1000时,得:x=20.
20-2=18(天).
故乙车间完成生产任务时需18天,与甲同时完成生产任务.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
