苏科版数学七年级下册第9章《因式分解》方法归纳 课件(共41张PPT)
文档属性
| 名称 | 苏科版数学七年级下册第9章《因式分解》方法归纳 课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 457.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 19:54:49 | ||
图片预览











文档简介
(共41张PPT)
因式分解 方法归纳
徐传新
专 题 因式分解
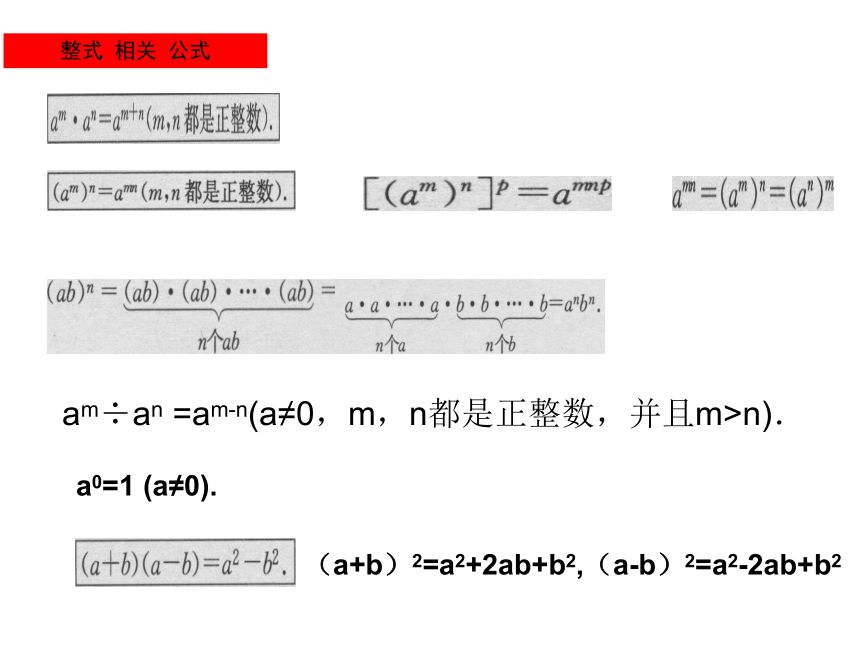
整式 相关 公式
am÷an =am-n(a≠0,m,n都是正整数,并且m>n).
a0=1 (a≠0).
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2
公式(a+b) (a-b) =a2 -b2的8种变化形式:
归纳:完全平方公式的常用形式:
(l)a2 +b2 = (a+b) 2 - 2ab= (a-b)2 +2ab;
(2) ab= [(a+b)2-(a2+b2)];
(5) (a+b) 2 = (a-b)2 +4ab;
(6) (a-b) 2 = (a+b)2 -4ab;
(7)ab=
因式分解
------(一) 提公因式法
课前预习
1. 把下列多项式写成整式乘积的形式:
(1)a 2+a= ;(2)x 2-1= .
2.下列变形:①a(x+y)=ax+ay;②x2-4x+4=x(x-4)+4;③10x2-5x=5x(2x-1);④x2-16+3x=(x+4)(x-4)+3x.其中属于因式分解的有 .
3.8a3b2与12ab3c的公因式是 .
4. 把下列各式分解因式:
(1)6mn 2+2mn;
(2)18xyz-12x 2y 2;
a(a+1)
(x+1)(x-1)
③
4ab 2
原式=2mn(3n+1)
原式=6xy(3z-2xy)
因式分解的概念
定义:把一个多项式化成几个整式的积的形式,这种
式子的变形叫做把这个多项式因式分解,也叫做把这
个多项式分解因式.
如:ax+ay=a(x+y),a 2-b 2=(a+b)(a-b),
a2+2ab+b 2=(a+b) 2,
x2+(a+b)x+ab=(x+a)(x+b),
am+an+bm+bn=(a+b)(m+n),…,都是因式分解.
注意: ①因式分解专指多项式的恒等变形,即等式的
左边必须是多项式.
提公因式法 分解因式
注意:(1)提公因式分解因式的关键是确定公因式.确定一个多项式的公因式时,要对数字系数和字母分别考虑:
①对 于数字系数如果是整数系数,取各项系数的最大公约数作为公因式的系数
②对于字母,需考虑两条:一条是取各项相同的字母;另一条是各相同字母的指数取其次数最低的.
(2)乘法分配律是提公因式法的依据,提公因式法实质
上是分配律的“逆用”,即
(3)提公因式法分解因式的一般步骤是:第一步找出公
因式;第二步提公因式并确定另一个因式.提公因式
时可用原多项式除的公因式,所得的商即为提公因式
后剩下的另一个因式.也可以用公因式分别去除原多
项式的每一项,求得剩下的另一个因式.例如:因式
分解8a 3b 2-12ab 2c,提公因式4ab 2时,用4ab 2分
别去除原多项式的每一项,得
(8a 3b 2÷4ab 2-12ab3c÷4ab 2)=2a 2-3bc,
即8a 3b 2-12ab3c=4ab2(2a2-3bc).
【例2】 运用提取公因式法分解因式.
(1)12a 2b 3+6a 2b 2-18a 3b 2;
(2)-27m 2n+9mn 2-18mn;
(3)5a 2(x-y)+10a(y-x);
(4)x(x-y) 2-y(y-x) 2;
(5)18(a-b) 3-12b(b-a) 2.
解析:(1)系数12,6,-18的最大公约数为6.相同字母
a,b的最低次幂为a2b2,公因式为6a2b2.12a2b3+6a2b2-
18a3b2=6a2b2(2b+1-3a).
注意括号内第二项应为1.
(2)当第一项系数为负时,应提出负号,括号内各项都变号,
公因式为-9mn.
-27m2n+9mn2-18mn =-9mn(3m-n+2) .
(3)∵y-x=-(x-y),
∴公因式为5a(x-y).
5a2(x-y)+10a(y-x)
=5a(x-y)(a-2).
(4)x(x-y) 2-y(y-x)2
=x(x-y)2-y(x-y) 2
=(x-y)2(x-y)
=(x-y)3
(5)18(a-b)3-12b(b-a)2
=18(a-b) 3-12b(a-b)2
=6(a-b)2(3a-3b-2b)
=6(a-b)2(3a-5b)
3. 把下列各式分解因式.
(1)ab+a+b+1; (2)-4m 3+16m2-26m;
?
(3)m(a-3)+2(3-a); (4)6a(b-a)2-2(a-b)3.
原式=a(b+1)+(b+1)
=(b+1)(a+1)
原式=-2m(2m2-8m+13)
原式=m(a-3)-2(a-3)
=(a-3)(m-2)
原式=6a(a-b)2-2(a-b)3
=2(a-b)2[3a-(a-b)]
=2(a-b)2(2a+b)
5.因式分解:
(1)x(x﹣y)﹣y(y﹣x);
(2)a2x2y﹣axy2.
原式=x(x﹣y)+y(x﹣y)
=(x+y)(x﹣y)
原式=axy(ax﹣y)
14.3.2 公式法(一)
课前预习
1.计算:852﹣152=( )
A.70 B.700 C.4900 D.7000
2.下列多项式中,能运用公式法因式分解的是( )
A.x2﹣xy B.x2+xy
C.x2+y2 D.x2﹣y2
3.分解因式:x2﹣4= .
4.若x2﹣9=(x﹣3)(x+a),则a= .
D
D
(x+2)(x﹣2)
3
课堂精讲
知识点.利用平方差公式分解因式
a 2-b 2=(a+b)(a-b),即两个数的平方差等于这两个数
的和与这两个数的差的积.
(1)把乘法公式中的平方差公式(a+b)(a-b)=a 2-b 2逆用,
即为因式分解的平方差公式.
(2)公式中所说的“两个数”是a,b,而不是a 2,b 2,其
中a,b可以是单项式,也可以是多项式.
(3)平方差公式的特点:①左边是二项式,两项都能写
成平方的形式,且符号相反;②右边是两个数的和与这
两个数的差的积,凡是符合平方差公式特点的二项式,
都可以运用平方差公式分解因式,如x 2-y 2,a 2-1,4x 2-
9,(b+c) 2- 4(a-b) 2 等.
【例】 把下列各式分解因式.
课堂精讲
(1)25m2-n2; (2)(x-y)2-1;
?
?
?
(3)16x-25x3y2; (4)x4-16.
原式=(5m+n)(5m-n)
原式=(x-y+1)(x-y-1)
原式=x(4+5xy)(4-5xy)
原式=(x2+4)(x+2)(x-2)
随堂检测
1.将x2﹣16分解因式正确的是( )
A.(x﹣4)2 B.(x﹣4)(x+4)
C.(x+8)(x﹣8) D.(x﹣4)2+8x
2.下列多项式中能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.5m2﹣20mn
C.﹣x2﹣y2 D.﹣x2+9
3.若a+b=2011,a﹣b=1,则a2﹣b2= .
4.计算:20142﹣20132= .
5.4x2﹣9= .
B
D
2011
4027
(2x﹣3)(2x+3)
14.3.3 公式法(二)
课前预习
1.分解因式a4﹣2a2+1的结果是( )
A.(a2+1)2 B.(a2﹣1)2
C.a2(a2﹣2) D.(a+1)2(a﹣1)2
2.当a=9时,代数式a2+2a+1的值为 .
3.x2+ x+ 是完全平方式.
4.(2014龙岩)因式分解:x2﹣4x+4= .
D
100
1
(x﹣2)2
课堂精讲
知识点.用完全平方公式分解因式
(1)把整式乘法的完全平方公式(a±b)2 =a2±2ab+b2
反过来,就得到
即两个数的平方和加上(或减去)这两个数的积的2
倍,等于这两个数的和(或差)的平方.
我们把a2 +2ab+b2和a2 -2ab+b2这样的式子叫做完全
平方式,利用完全平方公式可以把形如完全平方式的
多项式因式分解,
公式中的a,b可以是单项式,也可以是多项式.
(2)完全平方公式的特点
等号左边是三项式,其中首末两项分别是两个数(或
两个式子)的平方,且这两项的符号相同,中间一项
是这两个数(或两个式子)的积的2倍,符号正负均
可.
等号右边是这两个数(或两个式子)的和(或者差)
的平方,当中间的乘积项与首末两项符号相同时,是
和的平方;当中间的乘积项与首末两项的符号相反时,
是差的平方.
归纳:如果把乘法公式的等号两边互换位置,就可以得
到用于分解因式的公式,用来把某些具有特殊形式的多
项式分解因式,这种分解因式的方法叫做公式法.
【例】分解因式:(1)﹣x2+4xy﹣4y2
(2)(x﹣1)(x﹣3)+1.
解析:(1)先添加带符号的括号,再利用完全平方
公式分解因式即可.
(2)首先利用多项式乘法计算出
(x﹣1)(x﹣3)=x2﹣4x+3,再加上1后变形成
x2﹣4x+4,然后再利用完全平方公式进行分解即可.
(1)解:﹣x2+4xy﹣4y2,
=﹣(x2﹣4xy+4y2),
=﹣(x﹣2y)2.
(2)解:原式=x2﹣4x+3+1,
=x2﹣4x+4,
=(x﹣2)2.
1. 把下列各式分解因式.
(1)y2-4x(y-x); (2)(a2+b2)2-4a2b2.
原式=(y-2x)2
原式=(a+b)2(a-b)2
随堂检测
1.下列各式中,满足完全平方公式进行因式分解的是( )
A.2x2+4x+1 B.4x2﹣12xy+9y2
C.2x2+4xy+y2 D.x2﹣y2+2xy
2.把代数式x2﹣4x+4分解因式,下列结果中正确的是( )
A.(x+2)(x﹣2) B.(x+2)2
C.(x﹣4)2 D.(x﹣2)2
3.若a=2b﹣2,则a2﹣4ab+4b2的值是 .
4.如果多项式x2﹣6x+c可以分解为(x﹣3)2,那么c的值是 .
5.分解因式4x2﹣4x+1= .
B
D
4
9
(2x﹣1)2
十字相乘法
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(a+b)x+ab=(x+a)(x+b)
2
x
x
a
b
ax+bx=(a+b)x
x
2
ab
例1 分解因式 x -6x+8
2
解:x -6x+8
2
x
x
-2
-4
-4x-2x=-6x
=(x-2)(x-4)
例2:
步骤:
①竖分二次项与常数项
②交叉相乘,积相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
试一试:
小结:
用十字相乘法把形如
二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
=(x 3)(x 1)
=(x 3)(x 1)
=(y 4)(y 5)
=(t 4)(t 14)
+
+
-
+
-
-
-
+
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同
十字相乘法②
试因式分解6x2+7x+2。
这里就要用到十字相乘法(适用于二次三项式)。
既然是二次式,就可以写成(ax+b)(cx+d)的形式。
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
所以,需要将二次项系数与常数项分别拆成两个数的积,而这四个数中,两个数的积与另外两个数的积之和刚好等于一次项系数,那么因式分解就成功了。
= 17
3 x2 + 11 x + 10
6 x2 + 7 x + 2
2
3
1
2
4
+ 3
= 7
∴6x2+7x+2=(2x+1)(3x+2)
1
3
5
2
2
+ 15
= 11
1
3
2
5
5
+ 6
∴3x2+11x+10=(x+2)(3x+5)
= –6
5 x2 – 6 xy – 8 y2
试因式分解5x2–6xy–8y2。
这里仍然可以用十字相乘法。
1
5
–2
4
4
– 10
∴5x2–6xy–8y2 =(x–2y)(5x+4y)
简记口诀:
首尾分解,交叉相乘,求和凑中。
分解因式 3x -10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
分解因式 5x -17x-12
2
解:5x -17x-12
2
5x
x
+3
-4
-20x+3x=-17x
=(5x+3)(x-4)
小结
1.十字相乘法分解因式的公式:x2+(a+b)x+ab=(x+a)(x+b)
3.在用十字相乘法分解因式时,因为常数项的分解因数有多种情况,所以通常要经过多次的尝试才能确定采用哪组分解来进行分解因式。
2.能用十字相乘法来分解因式的二次三项式的系数的特点:常数项能分解成两个数的积,且这两个数的和恰好等于一次项的系数。
小结
(1)要将二次三项式x2 + px + q因式分解,就需要找到两个数a、b,使它们的积等于常数项q,和等于一次项系数p, 满足这两个条件便可以进行如下因式分解,即
x2 + px + q = x2 +(a + b)x + ab = (x + a)(x + b).
用十字交叉线表示: x +a
x +b
ax + bx = (a + b)x
(2)由于把x2 + px + q中的q分解成两个因数有多种情况,怎样才能找到两个合适的数,通常要经过多次的尝试才能确定采用哪种情况来进行因式分解.
因式分解 方法归纳
徐传新
专 题 因式分解
整式 相关 公式
am÷an =am-n(a≠0,m,n都是正整数,并且m>n).
a0=1 (a≠0).
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2
公式(a+b) (a-b) =a2 -b2的8种变化形式:
归纳:完全平方公式的常用形式:
(l)a2 +b2 = (a+b) 2 - 2ab= (a-b)2 +2ab;
(2) ab= [(a+b)2-(a2+b2)];
(5) (a+b) 2 = (a-b)2 +4ab;
(6) (a-b) 2 = (a+b)2 -4ab;
(7)ab=
因式分解
------(一) 提公因式法
课前预习
1. 把下列多项式写成整式乘积的形式:
(1)a 2+a= ;(2)x 2-1= .
2.下列变形:①a(x+y)=ax+ay;②x2-4x+4=x(x-4)+4;③10x2-5x=5x(2x-1);④x2-16+3x=(x+4)(x-4)+3x.其中属于因式分解的有 .
3.8a3b2与12ab3c的公因式是 .
4. 把下列各式分解因式:
(1)6mn 2+2mn;
(2)18xyz-12x 2y 2;
a(a+1)
(x+1)(x-1)
③
4ab 2
原式=2mn(3n+1)
原式=6xy(3z-2xy)
因式分解的概念
定义:把一个多项式化成几个整式的积的形式,这种
式子的变形叫做把这个多项式因式分解,也叫做把这
个多项式分解因式.
如:ax+ay=a(x+y),a 2-b 2=(a+b)(a-b),
a2+2ab+b 2=(a+b) 2,
x2+(a+b)x+ab=(x+a)(x+b),
am+an+bm+bn=(a+b)(m+n),…,都是因式分解.
注意: ①因式分解专指多项式的恒等变形,即等式的
左边必须是多项式.
提公因式法 分解因式
注意:(1)提公因式分解因式的关键是确定公因式.确定一个多项式的公因式时,要对数字系数和字母分别考虑:
①对 于数字系数如果是整数系数,取各项系数的最大公约数作为公因式的系数
②对于字母,需考虑两条:一条是取各项相同的字母;另一条是各相同字母的指数取其次数最低的.
(2)乘法分配律是提公因式法的依据,提公因式法实质
上是分配律的“逆用”,即
(3)提公因式法分解因式的一般步骤是:第一步找出公
因式;第二步提公因式并确定另一个因式.提公因式
时可用原多项式除的公因式,所得的商即为提公因式
后剩下的另一个因式.也可以用公因式分别去除原多
项式的每一项,求得剩下的另一个因式.例如:因式
分解8a 3b 2-12ab 2c,提公因式4ab 2时,用4ab 2分
别去除原多项式的每一项,得
(8a 3b 2÷4ab 2-12ab3c÷4ab 2)=2a 2-3bc,
即8a 3b 2-12ab3c=4ab2(2a2-3bc).
【例2】 运用提取公因式法分解因式.
(1)12a 2b 3+6a 2b 2-18a 3b 2;
(2)-27m 2n+9mn 2-18mn;
(3)5a 2(x-y)+10a(y-x);
(4)x(x-y) 2-y(y-x) 2;
(5)18(a-b) 3-12b(b-a) 2.
解析:(1)系数12,6,-18的最大公约数为6.相同字母
a,b的最低次幂为a2b2,公因式为6a2b2.12a2b3+6a2b2-
18a3b2=6a2b2(2b+1-3a).
注意括号内第二项应为1.
(2)当第一项系数为负时,应提出负号,括号内各项都变号,
公因式为-9mn.
-27m2n+9mn2-18mn =-9mn(3m-n+2) .
(3)∵y-x=-(x-y),
∴公因式为5a(x-y).
5a2(x-y)+10a(y-x)
=5a(x-y)(a-2).
(4)x(x-y) 2-y(y-x)2
=x(x-y)2-y(x-y) 2
=(x-y)2(x-y)
=(x-y)3
(5)18(a-b)3-12b(b-a)2
=18(a-b) 3-12b(a-b)2
=6(a-b)2(3a-3b-2b)
=6(a-b)2(3a-5b)
3. 把下列各式分解因式.
(1)ab+a+b+1; (2)-4m 3+16m2-26m;
?
(3)m(a-3)+2(3-a); (4)6a(b-a)2-2(a-b)3.
原式=a(b+1)+(b+1)
=(b+1)(a+1)
原式=-2m(2m2-8m+13)
原式=m(a-3)-2(a-3)
=(a-3)(m-2)
原式=6a(a-b)2-2(a-b)3
=2(a-b)2[3a-(a-b)]
=2(a-b)2(2a+b)
5.因式分解:
(1)x(x﹣y)﹣y(y﹣x);
(2)a2x2y﹣axy2.
原式=x(x﹣y)+y(x﹣y)
=(x+y)(x﹣y)
原式=axy(ax﹣y)
14.3.2 公式法(一)
课前预习
1.计算:852﹣152=( )
A.70 B.700 C.4900 D.7000
2.下列多项式中,能运用公式法因式分解的是( )
A.x2﹣xy B.x2+xy
C.x2+y2 D.x2﹣y2
3.分解因式:x2﹣4= .
4.若x2﹣9=(x﹣3)(x+a),则a= .
D
D
(x+2)(x﹣2)
3
课堂精讲
知识点.利用平方差公式分解因式
a 2-b 2=(a+b)(a-b),即两个数的平方差等于这两个数
的和与这两个数的差的积.
(1)把乘法公式中的平方差公式(a+b)(a-b)=a 2-b 2逆用,
即为因式分解的平方差公式.
(2)公式中所说的“两个数”是a,b,而不是a 2,b 2,其
中a,b可以是单项式,也可以是多项式.
(3)平方差公式的特点:①左边是二项式,两项都能写
成平方的形式,且符号相反;②右边是两个数的和与这
两个数的差的积,凡是符合平方差公式特点的二项式,
都可以运用平方差公式分解因式,如x 2-y 2,a 2-1,4x 2-
9,(b+c) 2- 4(a-b) 2 等.
【例】 把下列各式分解因式.
课堂精讲
(1)25m2-n2; (2)(x-y)2-1;
?
?
?
(3)16x-25x3y2; (4)x4-16.
原式=(5m+n)(5m-n)
原式=(x-y+1)(x-y-1)
原式=x(4+5xy)(4-5xy)
原式=(x2+4)(x+2)(x-2)
随堂检测
1.将x2﹣16分解因式正确的是( )
A.(x﹣4)2 B.(x﹣4)(x+4)
C.(x+8)(x﹣8) D.(x﹣4)2+8x
2.下列多项式中能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.5m2﹣20mn
C.﹣x2﹣y2 D.﹣x2+9
3.若a+b=2011,a﹣b=1,则a2﹣b2= .
4.计算:20142﹣20132= .
5.4x2﹣9= .
B
D
2011
4027
(2x﹣3)(2x+3)
14.3.3 公式法(二)
课前预习
1.分解因式a4﹣2a2+1的结果是( )
A.(a2+1)2 B.(a2﹣1)2
C.a2(a2﹣2) D.(a+1)2(a﹣1)2
2.当a=9时,代数式a2+2a+1的值为 .
3.x2+ x+ 是完全平方式.
4.(2014龙岩)因式分解:x2﹣4x+4= .
D
100
1
(x﹣2)2
课堂精讲
知识点.用完全平方公式分解因式
(1)把整式乘法的完全平方公式(a±b)2 =a2±2ab+b2
反过来,就得到
即两个数的平方和加上(或减去)这两个数的积的2
倍,等于这两个数的和(或差)的平方.
我们把a2 +2ab+b2和a2 -2ab+b2这样的式子叫做完全
平方式,利用完全平方公式可以把形如完全平方式的
多项式因式分解,
公式中的a,b可以是单项式,也可以是多项式.
(2)完全平方公式的特点
等号左边是三项式,其中首末两项分别是两个数(或
两个式子)的平方,且这两项的符号相同,中间一项
是这两个数(或两个式子)的积的2倍,符号正负均
可.
等号右边是这两个数(或两个式子)的和(或者差)
的平方,当中间的乘积项与首末两项符号相同时,是
和的平方;当中间的乘积项与首末两项的符号相反时,
是差的平方.
归纳:如果把乘法公式的等号两边互换位置,就可以得
到用于分解因式的公式,用来把某些具有特殊形式的多
项式分解因式,这种分解因式的方法叫做公式法.
【例】分解因式:(1)﹣x2+4xy﹣4y2
(2)(x﹣1)(x﹣3)+1.
解析:(1)先添加带符号的括号,再利用完全平方
公式分解因式即可.
(2)首先利用多项式乘法计算出
(x﹣1)(x﹣3)=x2﹣4x+3,再加上1后变形成
x2﹣4x+4,然后再利用完全平方公式进行分解即可.
(1)解:﹣x2+4xy﹣4y2,
=﹣(x2﹣4xy+4y2),
=﹣(x﹣2y)2.
(2)解:原式=x2﹣4x+3+1,
=x2﹣4x+4,
=(x﹣2)2.
1. 把下列各式分解因式.
(1)y2-4x(y-x); (2)(a2+b2)2-4a2b2.
原式=(y-2x)2
原式=(a+b)2(a-b)2
随堂检测
1.下列各式中,满足完全平方公式进行因式分解的是( )
A.2x2+4x+1 B.4x2﹣12xy+9y2
C.2x2+4xy+y2 D.x2﹣y2+2xy
2.把代数式x2﹣4x+4分解因式,下列结果中正确的是( )
A.(x+2)(x﹣2) B.(x+2)2
C.(x﹣4)2 D.(x﹣2)2
3.若a=2b﹣2,则a2﹣4ab+4b2的值是 .
4.如果多项式x2﹣6x+c可以分解为(x﹣3)2,那么c的值是 .
5.分解因式4x2﹣4x+1= .
B
D
4
9
(2x﹣1)2
十字相乘法
(x+a)(x+b)=x2+(a+b)x+ab
观察与发现
两个一次二项式相乘的积
一个二次三项式
整式的乘法
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数q能分解成两个因数a、b的积,而且一次项系数p又恰好是a+b,那么x2+px+q就可以进行如上的因式分解。
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x +(a+b)x+ab=(x+a)(x+b)
2
x
x
a
b
ax+bx=(a+b)x
x
2
ab
例1 分解因式 x -6x+8
2
解:x -6x+8
2
x
x
-2
-4
-4x-2x=-6x
=(x-2)(x-4)
例2:
步骤:
①竖分二次项与常数项
②交叉相乘,积相加
③检验确定,横写因式
十字相乘法(借助十字交叉线分解因式的方法)
顺口溜:
竖分常数交叉验,
横写因式不能乱。
试一试:
小结:
用十字相乘法把形如
二次三项式分解因式使
(顺口溜:竖分常数交叉验,横写因式不能乱。)
练一练:
小结:
用十字相乘法把形如
二次三项式分解因式
当q>0时,q分解的因数a、b( )
当q<0时, q分解的因数a、b( )
同号
异号
将下列各式分解因式
观察:p与a、b符号关系
小结:
当q>0时,q分解的因数a、b( )
同号
异号
当q<0时, q分解的因数a、b( )
且(a、b符号)与p符号相同
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
=(x 3)(x 1)
=(x 3)(x 1)
=(y 4)(y 5)
=(t 4)(t 14)
+
+
-
+
-
-
-
+
当q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符号相同
当q<0时, q分解的因数a、b( 异号) (其中绝对值较大的因数符号)与p符号相同
十字相乘法②
试因式分解6x2+7x+2。
这里就要用到十字相乘法(适用于二次三项式)。
既然是二次式,就可以写成(ax+b)(cx+d)的形式。
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
所以,需要将二次项系数与常数项分别拆成两个数的积,而这四个数中,两个数的积与另外两个数的积之和刚好等于一次项系数,那么因式分解就成功了。
= 17
3 x2 + 11 x + 10
6 x2 + 7 x + 2
2
3
1
2
4
+ 3
= 7
∴6x2+7x+2=(2x+1)(3x+2)
1
3
5
2
2
+ 15
= 11
1
3
2
5
5
+ 6
∴3x2+11x+10=(x+2)(3x+5)
= –6
5 x2 – 6 xy – 8 y2
试因式分解5x2–6xy–8y2。
这里仍然可以用十字相乘法。
1
5
–2
4
4
– 10
∴5x2–6xy–8y2 =(x–2y)(5x+4y)
简记口诀:
首尾分解,交叉相乘,求和凑中。
分解因式 3x -10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
分解因式 5x -17x-12
2
解:5x -17x-12
2
5x
x
+3
-4
-20x+3x=-17x
=(5x+3)(x-4)
小结
1.十字相乘法分解因式的公式:x2+(a+b)x+ab=(x+a)(x+b)
3.在用十字相乘法分解因式时,因为常数项的分解因数有多种情况,所以通常要经过多次的尝试才能确定采用哪组分解来进行分解因式。
2.能用十字相乘法来分解因式的二次三项式的系数的特点:常数项能分解成两个数的积,且这两个数的和恰好等于一次项的系数。
小结
(1)要将二次三项式x2 + px + q因式分解,就需要找到两个数a、b,使它们的积等于常数项q,和等于一次项系数p, 满足这两个条件便可以进行如下因式分解,即
x2 + px + q = x2 +(a + b)x + ab = (x + a)(x + b).
用十字交叉线表示: x +a
x +b
ax + bx = (a + b)x
(2)由于把x2 + px + q中的q分解成两个因数有多种情况,怎样才能找到两个合适的数,通常要经过多次的尝试才能确定采用哪种情况来进行因式分解.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
