中考数学二次函数综合题微复习学案(含简单答案)
文档属性
| 名称 | 中考数学二次函数综合题微复习学案(含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 246.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 21:51:33 | ||
图片预览



文档简介
微复习:二次函数综合题目总结(一):
二次函数综合题目历来被出题者青睐,现对基础题型及解法总结如下:
题型一:线段和最小:
我个人把它叫做一动(点)两定(点)问题。一般动点所在的位置有两种:一种是动点在对称轴上;一种是动点在坐标轴上。
这类题的解题思路是:找一定点关于动点所在直线的对称点,连接另一定点和对称点的线段就是所求线段。
变式题:找构成的三角形周长最小。解题思路为:三角形的三边中有一条边长固定,另两条边长不固定。不固定的按线段和最小的方法进行处理就好。
例1:如图,已知抛物线的对称轴为直线,且抛物线与轴交于A、B两点,与y轴交于C点,其中,.顶点为D
(1)在抛物线的对称轴上找一点,使点到点A的距离与到点C的距离之和最小,求出点的坐标;
(2)若点在x轴上,使点C+PD最小,求出点的坐标;
(3)在该抛物线的对称轴上,是否存在点N,使△ANC的周长最小?若存在,求出点N的坐标;若不存在,请说明理由;
题型二:线段最长:属于两个动点问题,
问题:过动点向x轴上作垂线,与一次函数图像和二次函数图像分别有交点,求这两个交点的长度的最值,就是此类问题。
解题思路是:用这两个交点的纵坐标相减(哪个交点在上,就用哪个交点纵坐标减去另一个交点纵坐标),得到一个二次函数解析式,求出最值即问题解决。抓好线段最长这条直线就可以解决有关面积最大的基本问题。
变式题:求围成的三角形面积最大时:以动点所在的线段为底,高为定值,根据三角形面积公式列出代数式,问题可解决;
求围成的四边形面积最大时:用分割法,把四边形分割成几个三角形的面积和(差)进行求解。
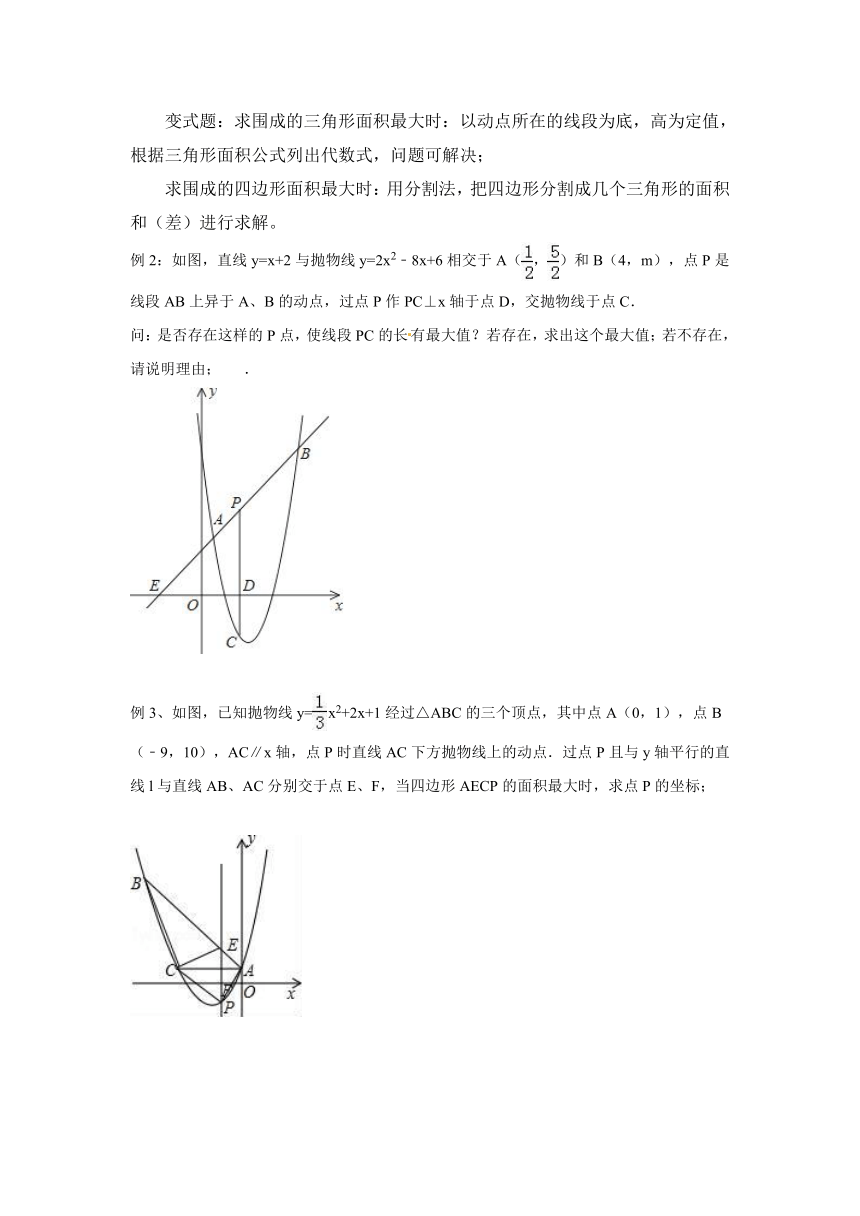
例2:如图,直线y=x+2与抛物线y=2x2﹣8x+6相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
问:是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由; .
例3、如图,已知抛物线y=x2+2x+1经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
题型三:形成特殊三角形:等腰三角形和直角三角形
解题思路是:用字母分别表示出构成三角形的三边的长度,
构成等腰三角形:分别让三边中的两条边两两相等;
构成直角三角形:分别让三边为斜边,根据勾股定理列出方程,即可。
若题目中有特殊要求的,按题目中的要求去做。
例4:如图,直线y=x+2与抛物线y=2x2﹣8x+6相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
问:求△PAC为直角三角形时点P的坐标.
例5:如图,已知二次函y=x2﹣2x﹣3的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
题型四:形成相似三角形:相似三角形存在的形式一般有:A字型和旋转型两种。
解题思路是:一般是利用两角对应相等,两三角形相似。判断角相等一般找公共角或线平行;特殊情况要依据:对应边成比例且夹角相等进行判定。
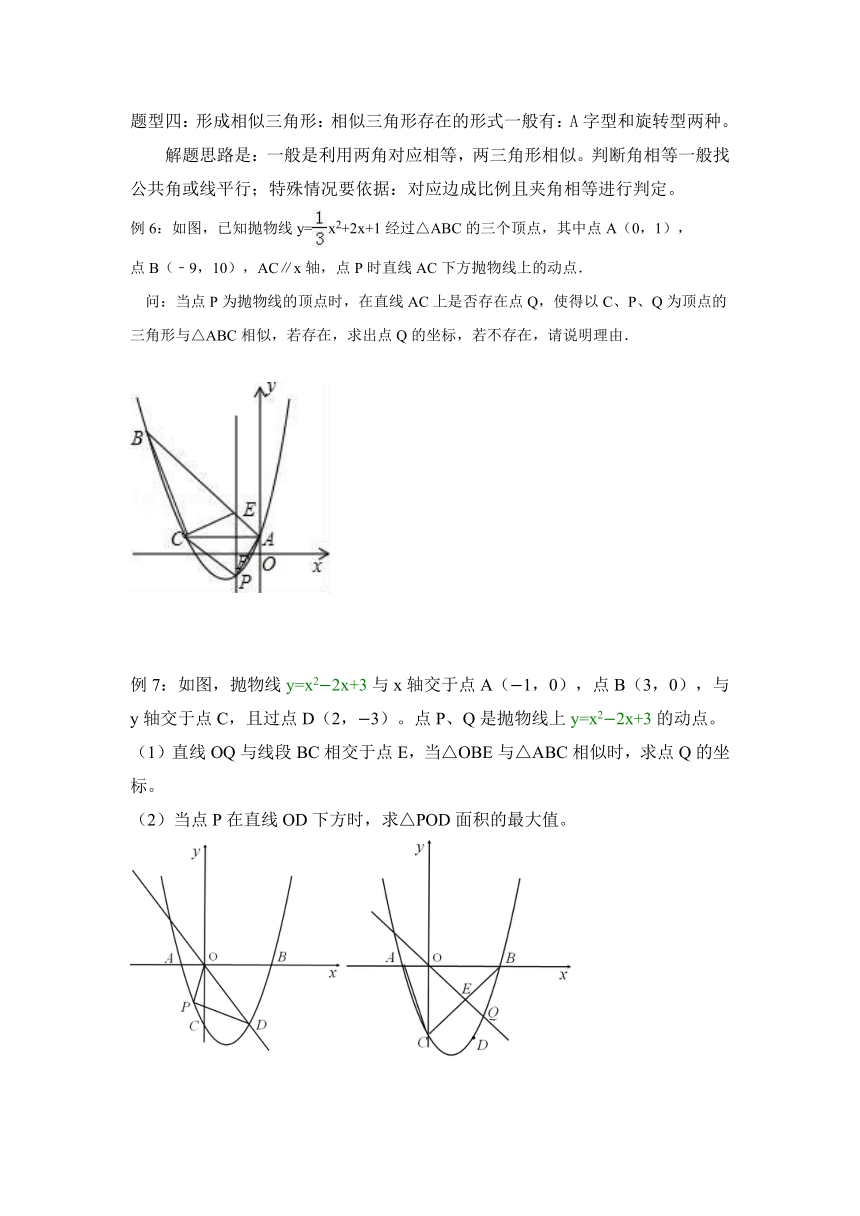
例6:如图,已知抛物线y=x2+2x+1经过△ABC的三个顶点,其中点A(0,1),
点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
问:当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
例7:如图,抛物线y=x2?2x+3与x轴交于点A(?1,0),点B(3,0),与y轴交于点C,且过点D(2,?3)。点P、Q是抛物线上y=x2?2x+3的动点。
(1)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标。
(2)当点P在直线OD下方时,求△POD面积的最大值。
题型五:形成特殊平行四边形:
解题思路是:利用特殊平行四边形对边分别相等且平行的性质进行判断。
讨论:动点所在的线段为对边和对角线两种情况。
例8:在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是
(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.若经过点C、A、A′,的抛物线的解析式为:y=﹣x2+3x+4;
问:若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标.
例9:已知抛物线y=-x2-2x+3经过点A(-3,0),B(1,0),C(0,3)三点.
问:过点C作y轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.
题型六:根据所给的两角相等,求对应的点的坐标:
解题思路是:一般的处理是,利用三角形相似,找到对应边的比进行解决
例:10:如图,抛物线与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
例11、如图,抛物线y=x2+bx+c与x轴交于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,3).如图,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标;
中考在线:
1、如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
2、如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,-5),对称轴为直线l,点M是线段AB的中点.
(1)求抛物线的表达式;
(2)写出点M的坐标并求出直线AB的表达式;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.
3、如图,抛物线y=x2-x-4与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,抛物线上一点D(1,-5),直线BD与y轴交于点E,动点M在线段BD上,当∠BDC=∠MCE时,求点M的坐标.
4、已知抛物线y=ax2+x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
(1)求抛物线的解析式和A,B两点的坐标;
(2)如图1,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;
(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M的坐标.
部分参考答案:
题型一:线段和最小;
题型二:线段最长: 例2: 当n=时,线段PC最大且为.
例3:当m=﹣时,四边形AECP的面积的最大值是,此时点P(﹣,﹣)
题型三:构成特殊的三角形
例4:△PAC为直角三角形时,点P的坐标为(3,5)或(,).
例5:当n=时,PM最大=; P(1,﹣4)或(,﹣2﹣1).
题型四:形成相似三角形:例6:Q(﹣4,1)Q(3,1).
例7:(1))Q1(,),Q2(,),Q3(,),Q4(,)。
(2)S△POD的最大值为
题型五:形成特殊平行四边形:
例8:点P的坐标为:P1(0,4),P2(3,4),P3(,﹣4),P4(,﹣4);
例9:正方形
题型六:根据所给的两角相等,例10:
例11:∴P1(,),P2(,)
中考在线:1、(1)抛物线表达式:y=﹣x2+x+4;
(2)△ABC是直角三角形.
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).
(4)当△AMN面积最大时,N点坐标为(3,0).
2、 y=2x-5.
P(6,1),Q(4,-3);∴P(2,1),Q(4,5);∴P(2,1),Q(4,1).
3、M(,-)
4、:y=﹣x2+x+4
存在点P,点P的坐标为(4,6),四边形PBOC面积的最大值为32.
点M的坐标为(4﹣2,﹣1)或(4+2,﹣﹣1).
二次函数综合题目历来被出题者青睐,现对基础题型及解法总结如下:
题型一:线段和最小:
我个人把它叫做一动(点)两定(点)问题。一般动点所在的位置有两种:一种是动点在对称轴上;一种是动点在坐标轴上。
这类题的解题思路是:找一定点关于动点所在直线的对称点,连接另一定点和对称点的线段就是所求线段。
变式题:找构成的三角形周长最小。解题思路为:三角形的三边中有一条边长固定,另两条边长不固定。不固定的按线段和最小的方法进行处理就好。
例1:如图,已知抛物线的对称轴为直线,且抛物线与轴交于A、B两点,与y轴交于C点,其中,.顶点为D
(1)在抛物线的对称轴上找一点,使点到点A的距离与到点C的距离之和最小,求出点的坐标;
(2)若点在x轴上,使点C+PD最小,求出点的坐标;
(3)在该抛物线的对称轴上,是否存在点N,使△ANC的周长最小?若存在,求出点N的坐标;若不存在,请说明理由;
题型二:线段最长:属于两个动点问题,
问题:过动点向x轴上作垂线,与一次函数图像和二次函数图像分别有交点,求这两个交点的长度的最值,就是此类问题。
解题思路是:用这两个交点的纵坐标相减(哪个交点在上,就用哪个交点纵坐标减去另一个交点纵坐标),得到一个二次函数解析式,求出最值即问题解决。抓好线段最长这条直线就可以解决有关面积最大的基本问题。
变式题:求围成的三角形面积最大时:以动点所在的线段为底,高为定值,根据三角形面积公式列出代数式,问题可解决;
求围成的四边形面积最大时:用分割法,把四边形分割成几个三角形的面积和(差)进行求解。
例2:如图,直线y=x+2与抛物线y=2x2﹣8x+6相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
问:是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由; .
例3、如图,已知抛物线y=x2+2x+1经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
题型三:形成特殊三角形:等腰三角形和直角三角形
解题思路是:用字母分别表示出构成三角形的三边的长度,
构成等腰三角形:分别让三边中的两条边两两相等;
构成直角三角形:分别让三边为斜边,根据勾股定理列出方程,即可。
若题目中有特殊要求的,按题目中的要求去做。
例4:如图,直线y=x+2与抛物线y=2x2﹣8x+6相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
问:求△PAC为直角三角形时点P的坐标.
例5:如图,已知二次函y=x2﹣2x﹣3的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
题型四:形成相似三角形:相似三角形存在的形式一般有:A字型和旋转型两种。
解题思路是:一般是利用两角对应相等,两三角形相似。判断角相等一般找公共角或线平行;特殊情况要依据:对应边成比例且夹角相等进行判定。
例6:如图,已知抛物线y=x2+2x+1经过△ABC的三个顶点,其中点A(0,1),
点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
问:当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
例7:如图,抛物线y=x2?2x+3与x轴交于点A(?1,0),点B(3,0),与y轴交于点C,且过点D(2,?3)。点P、Q是抛物线上y=x2?2x+3的动点。
(1)直线OQ与线段BC相交于点E,当△OBE与△ABC相似时,求点Q的坐标。
(2)当点P在直线OD下方时,求△POD面积的最大值。
题型五:形成特殊平行四边形:
解题思路是:利用特殊平行四边形对边分别相等且平行的性质进行判断。
讨论:动点所在的线段为对边和对角线两种情况。
例8:在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是
(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.若经过点C、A、A′,的抛物线的解析式为:y=﹣x2+3x+4;
问:若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标.
例9:已知抛物线y=-x2-2x+3经过点A(-3,0),B(1,0),C(0,3)三点.
问:过点C作y轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.
题型六:根据所给的两角相等,求对应的点的坐标:
解题思路是:一般的处理是,利用三角形相似,找到对应边的比进行解决
例:10:如图,抛物线与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.若点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
例11、如图,抛物线y=x2+bx+c与x轴交于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,3).如图,连接AC,点P在抛物线上,且满足∠PAB=2∠ACO,求点P的坐标;
中考在线:
1、如图1,已知二次函数y=ax2+x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
2、如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,-5),对称轴为直线l,点M是线段AB的中点.
(1)求抛物线的表达式;
(2)写出点M的坐标并求出直线AB的表达式;
(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.
3、如图,抛物线y=x2-x-4与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,抛物线上一点D(1,-5),直线BD与y轴交于点E,动点M在线段BD上,当∠BDC=∠MCE时,求点M的坐标.
4、已知抛物线y=ax2+x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.
(1)求抛物线的解析式和A,B两点的坐标;
(2)如图1,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由;
(3)如图2,若点M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求点M的坐标.
部分参考答案:
题型一:线段和最小;
题型二:线段最长: 例2: 当n=时,线段PC最大且为.
例3:当m=﹣时,四边形AECP的面积的最大值是,此时点P(﹣,﹣)
题型三:构成特殊的三角形
例4:△PAC为直角三角形时,点P的坐标为(3,5)或(,).
例5:当n=时,PM最大=; P(1,﹣4)或(,﹣2﹣1).
题型四:形成相似三角形:例6:Q(﹣4,1)Q(3,1).
例7:(1))Q1(,),Q2(,),Q3(,),Q4(,)。
(2)S△POD的最大值为
题型五:形成特殊平行四边形:
例8:点P的坐标为:P1(0,4),P2(3,4),P3(,﹣4),P4(,﹣4);
例9:正方形
题型六:根据所给的两角相等,例10:
例11:∴P1(,),P2(,)
中考在线:1、(1)抛物线表达式:y=﹣x2+x+4;
(2)△ABC是直角三角形.
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4,0)、(3,0)、(8+4,0).
(4)当△AMN面积最大时,N点坐标为(3,0).
2、 y=2x-5.
P(6,1),Q(4,-3);∴P(2,1),Q(4,5);∴P(2,1),Q(4,1).
3、M(,-)
4、:y=﹣x2+x+4
存在点P,点P的坐标为(4,6),四边形PBOC面积的最大值为32.
点M的坐标为(4﹣2,﹣1)或(4+2,﹣﹣1).
同课章节目录
