人教版高二物理选修3-1第一章 第9节 带电粒子在电场中的运动(共54张PPT)
文档属性
| 名称 | 人教版高二物理选修3-1第一章 第9节 带电粒子在电场中的运动(共54张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-09 17:31:58 | ||
图片预览








文档简介
(共54张PPT)
第九节 带电粒子在电场中的运动
本节内容建议2~3课时完成
知识储备
(1)牛顿第二定律的内容是什么?
(2)动能定理的表达式是什么?
(3)平抛运动的相关知识点。
(4)静电力做功的计算方法。
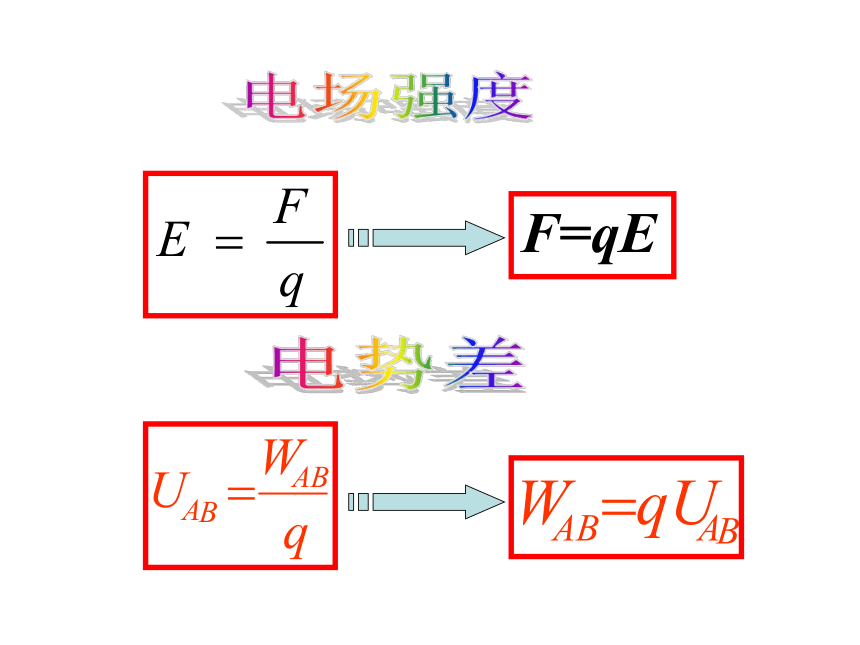
F=qE
学习运用电场强度、电场力等概念研究带电粒子在电场中运动时的加速度、速度、位移等物理量的变化;
学习运用电势差、电场力做功等概念研究带电粒子在电场中运动时的能量的转化.
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和电场力相比小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
电场的基本性质是: 对放入
电场中的电荷有力的作用。
电荷会有加速度。
加速度a可能是恒定的也可
能是变化的。
速度v 的大小和方向都有可
能发生变化。
轨迹既可能是直线也可能是曲线。
a 。
v 。
轨迹 。
增大
增大
直线
a 。
v 。
轨迹 。
减小
减小
曲线
带电粒子在匀强电场中
运动情况:
受到恒定的电场力
受力情况:
做匀变速运动
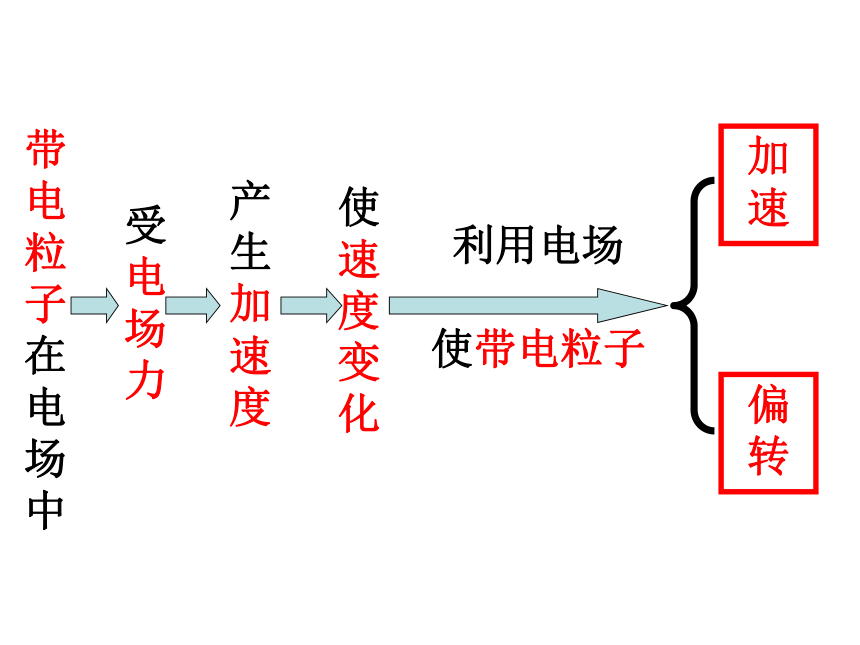
带电粒子在电场中
受电场力
产生加速度
使速度变化
利用电场
使带电粒子
加速
偏转
一、带电粒子在电场中的加速
两板间电势差为U
质量为 m 电量为 q 的粒子。
从正极板静止开始运动,求到
达负极板时的速度。
探究思路
静电力做的功:
设末速度为 v ,由动能定理:
①
②
由①②可得:
变换已知条件
两板间电势差:
③
由①②③可得:
思考
如两极板间不是匀强电场该用何种方法求解?为什么?
由于电场力做功与场强是否匀强无关,与运动路径也无关,第二种方法仍适用!
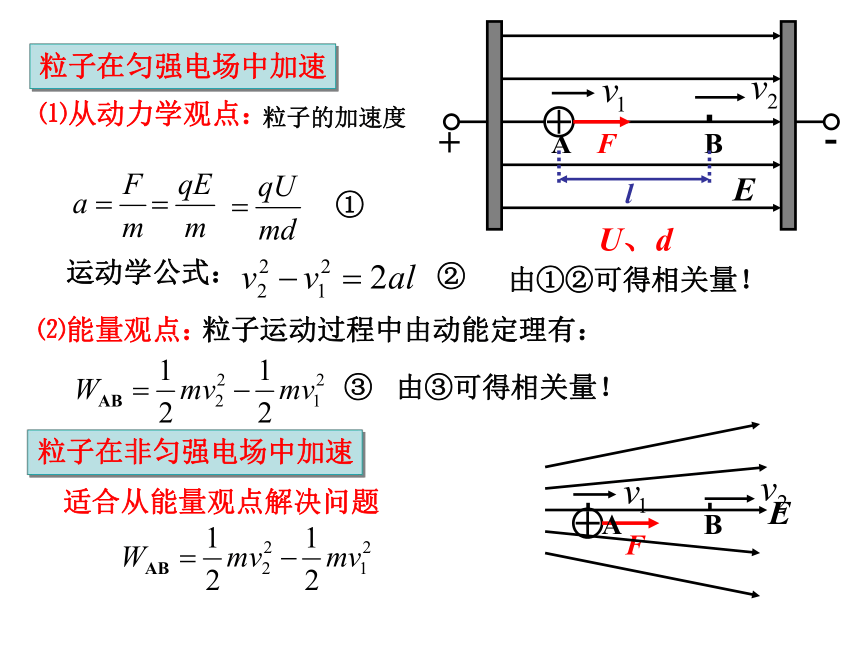
粒子在匀强电场中加速
⑴从动力学观点:
粒子的加速度
U、d
l
运动学公式:
①
②
由①②可得相关量!
⑵能量观点:
粒子运动过程中由动能定理有:
由③可得相关量!
粒子在非匀强电场中加速
适合从能量观点解决问题
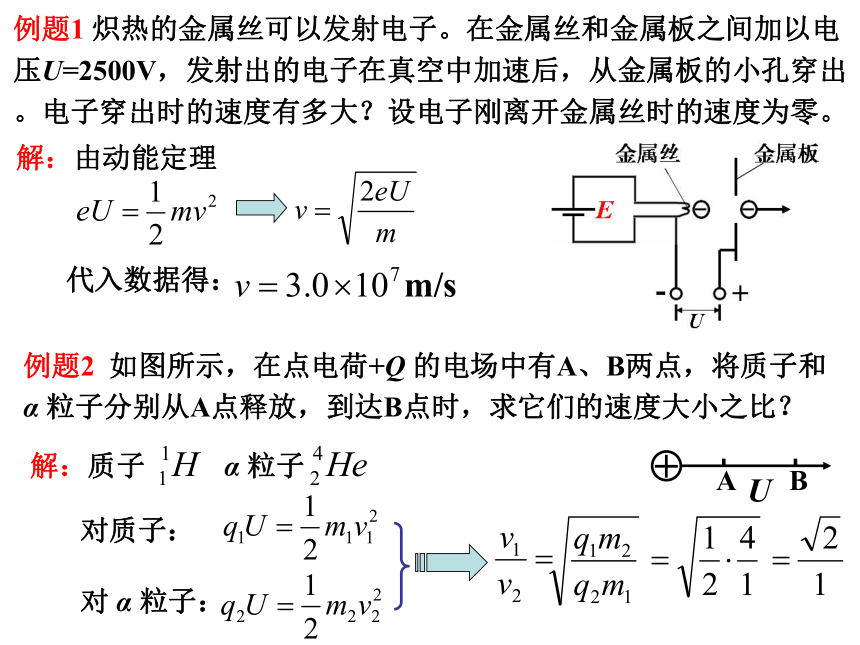
例题1 炽热的金属丝可以发射电子。在金属丝和金属板之间加以电
压U=2500V,发射出的电子在真空中加速后,从金属板的小孔穿出
。电子穿出时的速度有多大?设电子刚离开金属丝时的速度为零。
解:由动能定理
代入数据得:
例题2 如图所示,在点电荷+Q 的电场中有A、B两点,将质子和
α 粒子分别从A点释放,到达B点时,求它们的速度大小之比?
对质子:
U
对 α 粒子:
1、下列粒子由静止经加速电压为U的电场加速后, 哪种粒子动能最大 ( )
哪种粒子速度最大 ( )
A、质子 B、电子 C、氘核 D、氦核
自主训练
与电量成正比
与比荷平方根成正比
2、如图所示,M、N是在真空中竖直放置的两块平行金属板,质量为m、电量为+q的带电粒子,以极小的初速度由小孔进入电场,当M、N间电压为U时,粒子到达N板的速度为v,如果要使这个带电粒子到达N板的速度为2v ,则下述方法能满足要求的是( ) A、使M、N间电压增加为2U B、使M、N间电压增加为4U C、使M、N间电压不变,距离减半 D、使M、N间电压不变,距离加倍
M
N
U
d
v与电压平方根成正比
自主训练
3、如图M、N是在真空中竖直放置的两块平行金属板,质量为m电量为-q的带电粒子,以初速度V0由小孔进入电场,当M、N间电压为U时,粒子刚好能到达N板,如果要使这个带电粒子能够到达M、N两板间距的1/2处返回,则下述方法能满足要求的是( ) A、使初速度减半 B、使M、N间电压加倍 C、使M、N间电压提高4倍 D、使初速度和M、N间电压都加倍
M
N
U
d
-
v0
自主训练
4、如图所示的电场中有A、B两点,A、B的电势差UAB=100V,一个质量为m=2.0×10-12kg、电量为q=-5.0×10-8C的带电粒子,以初速度v0 =3.0×103m/s由A点运动到B点,求粒子到达B点时的速率。(不计粒子重力)
q为负
自主训练
5、如图所示,A、B为平行金属板电容器,两板间的距离为d,在A板的缺口的正上方距离为h的P处,有一静止的、质量为m、带电量为+q的液滴由静止开始自由落下,若要使液滴不落在B板上,两板间场强至少为多大?两板间的电压U至少为多大?
mg
mg
qE
对全过程由动能定理:
自主训练
二、带电粒子在匀强电场中的偏转
d
U
v0
q、m
d
U
v0
q、m
F
v
v0
vy
y
θ
偏转角
侧移
二、带电粒子在匀强电场中的偏转
类平抛运动
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
二、带电粒子在匀强电场中的偏转
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
类平抛运动
二、带电粒子在匀强电场中的偏转
例题3 两个相同极板Y与 Y’ 的长度l=6.0cm ,相距d =2cm,极板间
的电压U=200V。一个电子沿平行于板面的方向射入电场中,射入时
的速度v0=3.0×107m/s 。把两板间的电场看做匀强电场,求电子射
出电场时沿垂直于板面方向偏移的距离y 和偏转的角度θ 。
解:电子在垂直于板面方向的加速度
电子在极板间运动的时间 t
①
②
电子垂直于极板方向的偏移距离 y
③
由①②③得:
偏转的角度θ
例题4 有一质量为m 带电荷+q 的粒子经电压U0加速后,进入两块间距为d,长度为l 的平行金属板,板间电压为U,求电荷的偏移量y和偏转角θ 。
解:设电荷进入偏转电场时速度大小为
V0 ,则
①
电荷在偏转电场中加速度为a
②
电荷在偏转电场中运动时间为t
③
偏移量:
④
注: 不同的带电粒子被同一电场加速后进入偏转电场, 运动情景一样!
例题5 如图所示,a、b、c表示点电荷的电场中的三个等势面,它们的电势分别为 , , 。一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c处时的速率为( )
A.
B.
C.
D.
解析: 电荷从a 到b,由动能定理有
电荷从b 到c,由动能定理有
C
例题6 如图,水平放置的两平行金属板,板长为l、板间距为d,一束电子以v0的初速度从两板中央水平射入板间,然后从板间飞出射到距板、宽D 的荧光屏上(荧光屏中点在两板中垂线上)。
⑴电子飞入两板前所经历的加速电场的电压多大?
⑵为了使电子能射至荧光屏上,求图中D应满足的条件?
⑶为了使电子能射至荧光屏上,求偏转电压UAB的范围?
解:⑴设加速电压为U1,则
⑵电子的最大偏移量为d/2
O
得:
A
B
⑶电子达到荧光屏边缘
,对应的偏转电压最大。
6、质量为m、带电量为q的粒子以初速度v从中线垂直进入偏转电场,刚好离开电场,它在离开电场后偏转角正切为0.5,则下列说法中正确的是( )
A、如果偏转电场的电压为原来的一半,则粒子离开电场后的偏转角正切为0.25
B、如果带电粒子的比荷为原来的一半,则粒子离开电场后的偏转角正切为0.25
C、如果带电粒子的初速度为原来的2倍,则粒子离开电场后的偏转角正切为0.25
D、如果带电粒子的初动能为原来的2倍,则粒子离开电场后的偏转角正切为0.25
自主训练
偏转角正切与比荷成正比
偏转角正切与初动能成反比
偏转角正切与电压成正比
7、质子(质量为m、电量为e)和二价氦离子(质量为4m、电量为2e)以相同的初动能垂直射入同一偏转电场中,离开电场后,它们的偏转角正切之比为 ,侧移之比为 。
与电量成正比
与电量成正比
自主训练
8、三个电子在同一地点沿同一直线垂直飞入偏转电场,如图所示。则由此可判断( )
A、 b和c同时飞离电场
B、在b飞离电场的瞬间,a刚好打在下极板上
C、进入电场时,c速度最大,a速度最小
D、c的动能增量最小,a和b的动能增量一样大
自主训练
分析与解答
9、如图,电子在电势差为U1的加速电场中由静止开始加速,然后射入电势差为U2的两块平行极板间的电场中,入射方向跟极板平行。整个装置处在真空中,重力可忽略。在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是 ( )
A、U1变大、U2变大 B、U1变小、U2变大
C、U1变大、U2变小 D、U1变小、U2变小
自主训练
对加速过程由动能定理:
对偏转过程由偏转角正切公式:
与粒子的电量q、质量m无关
分析与解答
10、如图所示,二价氦离子和质子的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,则它们( )
A、侧移相同
B、偏转角相同
C、到达屏上同一点
D、到达屏上不同点
与粒子的电量q、质量m无关
自主训练
11、试证明:带电粒子垂直进入偏转电场,离开电场时就好象是从初速度所在直线的中点沿直线离开电场的。
θ
x
自主训练
12、如图所示,有一电子(电量为e、质量为m)经电压U0加速后,沿平行金属板A、B中心线进入两板,A、B板间距为d、长度为L, A、B板间电压为U,屏CD足够大,距离A、B板右边缘2L,AB板的中心线过屏CD的中心且与屏CD垂直。试求电子束打在屏上的位置到屏中心间的距离。
自主训练
电子离开电场,就好象从中点沿直线离开的:
θ
对加速过程由动能定理:
分析与解答
13、质量为1×10-25kg、电量为1×10-16C的带电粒子以2×106m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间,如图所示。已知板长L=10cm,间距d=2cm,当AB间电压在 范围内时,此带电粒子能从板间飞出。
自主训练
v0
+ + + + +
- - - - -
θ
对偏转过程由偏转角正切公式:
或对偏转过程由侧移公式:
分析与解答
14、初速度为2×107m/s的电子沿平行金属板间的中心线射入板中,板长为30cm,相距为4cm,在两板间加上如图所示的正弦交变电压。已知电子的质量为9×10-31Kg,电量为1.6×10-19C,不计电子重力,求:要使所有的电子都能离开电场,图中电压的最大值U0需满足什么条件?
自主训练
可认为在t时间内电场不变
设电子在两板间的运动时间为t
设电子在偏转电压为U0时进入板间
分析与解答
?带电粒子在交变电场中的运动
在两个相互平行的金属板间加交变电压时,在两板间便可获得交变电场。此类电场从空间看是匀强电场,即同一时刻,电场中各个位置处电场强度的大小、方向都相同;从时间上看是变化的,即电场强度的大小、方向都可随时间变化。
研究带电粒子在这种交变电场中的运动, 关键是根据电场变化的特点,正确地判断粒子的运动情况。
当带电粒子通过电场的时间远远小于电场变化的周期时,可认为电场强度的大小、方向都不变。
小 结
产生高速飞行的电子束
使电子沿x方向偏移
※四、示波器的原理
使电子沿y方向
偏移
示波器是一种用来观察电信号随时间变化的电子仪器。
核心部件:
由电子枪、偏转电极和荧光屏组成,管内抽成真空。
示波管
电子枪部分:
偏转电极部分:
荧光屏部分:
发射出电子
使电子沿两方向偏转
电子使荧光物质受激而发光
※四、示波器的原理
※思考与讨论:
电子将打在光屏上的哪一点?
试在图中标出来。
电子将打在光屏上的哪一点?
试在图中标出来。
如果信号电压是周期性的,并且扫描电压与信号电压周期相同,就可以在荧光屏上出现稳定的图象了。
※15、如图所示的示波管,如果在YY’之间加如图所示的交变电压,同时在XX’之间加如图所示的锯齿形电压,使X的电势比X’高,在荧光屏上会看到什么图形?
自主训练
※15、如图所示的示波管,如果在YY’之间加如图所示的交变电压,同时在XX’之间加如图所示的锯齿形电压,使X的电势比X’高,在荧光屏上会看到什么图形?
X
Y
O
0t1自主训练
※16、真空室中电极K发出电子(初速不计),经过电压为U1的加速电场后,由小孔S沿水平金属板A、B间的中心线射入板中,板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,已知电子的质量为m,带电量为e,不计电子重力,求:
(1)电子进入AB板时的初速度;?
(2)要使所有的电子都能离开AB板,图乙中电压的最大值U0需满足什么条件?
(3)在荧光屏上
会看到什么图形?
自主训练
设电子进入AB板时的初速度为v0
设电子在偏转电压为U0时进入AB板间
分析与解答
1、研究带电粒子在电场中运动的两条主要线索
(1)力和运动的关系——牛顿第二定律
根据带电粒子受到的电场力,用牛顿第二定律找出加速度,结合运动学公式确定带电粒子的速度、位移等.这条线索通常适用于恒力作用下做匀变速运动的情况.
(2)功和能的关系——动能定理
根据电场力对带电粒子所做的功,引起带电粒子的能量发生变化,利用动能定理或从全过程中能量的转化,研究带电粒子的速度变化,经历的位移等.这条线索同样也适用于不均匀的电场.
2、研究带电粒子在电场中运动的两类重要的思维技巧
(1)类比与等效
电场力和重力都是恒力,在电场力作用下的运动可与重力作用下的运动类比.例如,垂直射入平行板电场中的带电粒子的运动可类比于平抛,带电单摆在竖直方向匀强电场中的运动可等效于重力场强度g值的变化等.
(2)整体法(全过程法)
电荷间的相互作用是成对出现的,把电荷系统的整体作为研究对象,就可以不必考虑其间的相互作用.
电场力的功与重力的功一样,都只与始末位置有关,与路径无关.它们分别引起电荷电势能的变化和重力势能的变化,从电荷运动的全过程中功能关系出发(尤其从静止出发末速度为零的问题)往往能迅速找到解题入口或简化计算.
2、研究带电粒子在电场中运动的两类重要的思维技巧
第九节 带电粒子在电场中的运动
本节内容建议2~3课时完成
知识储备
(1)牛顿第二定律的内容是什么?
(2)动能定理的表达式是什么?
(3)平抛运动的相关知识点。
(4)静电力做功的计算方法。
F=qE
学习运用电场强度、电场力等概念研究带电粒子在电场中运动时的加速度、速度、位移等物理量的变化;
学习运用电势差、电场力做功等概念研究带电粒子在电场中运动时的能量的转化.
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
电场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和电场力相比小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
电场的基本性质是: 对放入
电场中的电荷有力的作用。
电荷会有加速度。
加速度a可能是恒定的也可
能是变化的。
速度v 的大小和方向都有可
能发生变化。
轨迹既可能是直线也可能是曲线。
a 。
v 。
轨迹 。
增大
增大
直线
a 。
v 。
轨迹 。
减小
减小
曲线
带电粒子在匀强电场中
运动情况:
受到恒定的电场力
受力情况:
做匀变速运动
带电粒子在电场中
受电场力
产生加速度
使速度变化
利用电场
使带电粒子
加速
偏转
一、带电粒子在电场中的加速
两板间电势差为U
质量为 m 电量为 q 的粒子。
从正极板静止开始运动,求到
达负极板时的速度。
探究思路
静电力做的功:
设末速度为 v ,由动能定理:
①
②
由①②可得:
变换已知条件
两板间电势差:
③
由①②③可得:
思考
如两极板间不是匀强电场该用何种方法求解?为什么?
由于电场力做功与场强是否匀强无关,与运动路径也无关,第二种方法仍适用!
粒子在匀强电场中加速
⑴从动力学观点:
粒子的加速度
U、d
l
运动学公式:
①
②
由①②可得相关量!
⑵能量观点:
粒子运动过程中由动能定理有:
由③可得相关量!
粒子在非匀强电场中加速
适合从能量观点解决问题
例题1 炽热的金属丝可以发射电子。在金属丝和金属板之间加以电
压U=2500V,发射出的电子在真空中加速后,从金属板的小孔穿出
。电子穿出时的速度有多大?设电子刚离开金属丝时的速度为零。
解:由动能定理
代入数据得:
例题2 如图所示,在点电荷+Q 的电场中有A、B两点,将质子和
α 粒子分别从A点释放,到达B点时,求它们的速度大小之比?
对质子:
U
对 α 粒子:
1、下列粒子由静止经加速电压为U的电场加速后, 哪种粒子动能最大 ( )
哪种粒子速度最大 ( )
A、质子 B、电子 C、氘核 D、氦核
自主训练
与电量成正比
与比荷平方根成正比
2、如图所示,M、N是在真空中竖直放置的两块平行金属板,质量为m、电量为+q的带电粒子,以极小的初速度由小孔进入电场,当M、N间电压为U时,粒子到达N板的速度为v,如果要使这个带电粒子到达N板的速度为2v ,则下述方法能满足要求的是( ) A、使M、N间电压增加为2U B、使M、N间电压增加为4U C、使M、N间电压不变,距离减半 D、使M、N间电压不变,距离加倍
M
N
U
d
v与电压平方根成正比
自主训练
3、如图M、N是在真空中竖直放置的两块平行金属板,质量为m电量为-q的带电粒子,以初速度V0由小孔进入电场,当M、N间电压为U时,粒子刚好能到达N板,如果要使这个带电粒子能够到达M、N两板间距的1/2处返回,则下述方法能满足要求的是( ) A、使初速度减半 B、使M、N间电压加倍 C、使M、N间电压提高4倍 D、使初速度和M、N间电压都加倍
M
N
U
d
-
v0
自主训练
4、如图所示的电场中有A、B两点,A、B的电势差UAB=100V,一个质量为m=2.0×10-12kg、电量为q=-5.0×10-8C的带电粒子,以初速度v0 =3.0×103m/s由A点运动到B点,求粒子到达B点时的速率。(不计粒子重力)
q为负
自主训练
5、如图所示,A、B为平行金属板电容器,两板间的距离为d,在A板的缺口的正上方距离为h的P处,有一静止的、质量为m、带电量为+q的液滴由静止开始自由落下,若要使液滴不落在B板上,两板间场强至少为多大?两板间的电压U至少为多大?
mg
mg
qE
对全过程由动能定理:
自主训练
二、带电粒子在匀强电场中的偏转
d
U
v0
q、m
d
U
v0
q、m
F
v
v0
vy
y
θ
偏转角
侧移
二、带电粒子在匀强电场中的偏转
类平抛运动
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
二、带电粒子在匀强电场中的偏转
与粒子比荷q/m成正比
与粒子初速度v0平方成反比
与电场的属性U、l、d有关
类平抛运动
二、带电粒子在匀强电场中的偏转
例题3 两个相同极板Y与 Y’ 的长度l=6.0cm ,相距d =2cm,极板间
的电压U=200V。一个电子沿平行于板面的方向射入电场中,射入时
的速度v0=3.0×107m/s 。把两板间的电场看做匀强电场,求电子射
出电场时沿垂直于板面方向偏移的距离y 和偏转的角度θ 。
解:电子在垂直于板面方向的加速度
电子在极板间运动的时间 t
①
②
电子垂直于极板方向的偏移距离 y
③
由①②③得:
偏转的角度θ
例题4 有一质量为m 带电荷+q 的粒子经电压U0加速后,进入两块间距为d,长度为l 的平行金属板,板间电压为U,求电荷的偏移量y和偏转角θ 。
解:设电荷进入偏转电场时速度大小为
V0 ,则
①
电荷在偏转电场中加速度为a
②
电荷在偏转电场中运动时间为t
③
偏移量:
④
注: 不同的带电粒子被同一电场加速后进入偏转电场, 运动情景一样!
例题5 如图所示,a、b、c表示点电荷的电场中的三个等势面,它们的电势分别为 , , 。一带电粒子从等势面a上某处由静止释放后,仅受电场力作用而运动,已知它经过等势面b时的速率为vb,则它经过等势面c处时的速率为( )
A.
B.
C.
D.
解析: 电荷从a 到b,由动能定理有
电荷从b 到c,由动能定理有
C
例题6 如图,水平放置的两平行金属板,板长为l、板间距为d,一束电子以v0的初速度从两板中央水平射入板间,然后从板间飞出射到距板、宽D 的荧光屏上(荧光屏中点在两板中垂线上)。
⑴电子飞入两板前所经历的加速电场的电压多大?
⑵为了使电子能射至荧光屏上,求图中D应满足的条件?
⑶为了使电子能射至荧光屏上,求偏转电压UAB的范围?
解:⑴设加速电压为U1,则
⑵电子的最大偏移量为d/2
O
得:
A
B
⑶电子达到荧光屏边缘
,对应的偏转电压最大。
6、质量为m、带电量为q的粒子以初速度v从中线垂直进入偏转电场,刚好离开电场,它在离开电场后偏转角正切为0.5,则下列说法中正确的是( )
A、如果偏转电场的电压为原来的一半,则粒子离开电场后的偏转角正切为0.25
B、如果带电粒子的比荷为原来的一半,则粒子离开电场后的偏转角正切为0.25
C、如果带电粒子的初速度为原来的2倍,则粒子离开电场后的偏转角正切为0.25
D、如果带电粒子的初动能为原来的2倍,则粒子离开电场后的偏转角正切为0.25
自主训练
偏转角正切与比荷成正比
偏转角正切与初动能成反比
偏转角正切与电压成正比
7、质子(质量为m、电量为e)和二价氦离子(质量为4m、电量为2e)以相同的初动能垂直射入同一偏转电场中,离开电场后,它们的偏转角正切之比为 ,侧移之比为 。
与电量成正比
与电量成正比
自主训练
8、三个电子在同一地点沿同一直线垂直飞入偏转电场,如图所示。则由此可判断( )
A、 b和c同时飞离电场
B、在b飞离电场的瞬间,a刚好打在下极板上
C、进入电场时,c速度最大,a速度最小
D、c的动能增量最小,a和b的动能增量一样大
自主训练
分析与解答
9、如图,电子在电势差为U1的加速电场中由静止开始加速,然后射入电势差为U2的两块平行极板间的电场中,入射方向跟极板平行。整个装置处在真空中,重力可忽略。在满足电子能射出平行板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是 ( )
A、U1变大、U2变大 B、U1变小、U2变大
C、U1变大、U2变小 D、U1变小、U2变小
自主训练
对加速过程由动能定理:
对偏转过程由偏转角正切公式:
与粒子的电量q、质量m无关
分析与解答
10、如图所示,二价氦离子和质子的混合体,经同一加速电场加速后,垂直射入同一偏转电场中,偏转后,打在同一荧光屏上,则它们( )
A、侧移相同
B、偏转角相同
C、到达屏上同一点
D、到达屏上不同点
与粒子的电量q、质量m无关
自主训练
11、试证明:带电粒子垂直进入偏转电场,离开电场时就好象是从初速度所在直线的中点沿直线离开电场的。
θ
x
自主训练
12、如图所示,有一电子(电量为e、质量为m)经电压U0加速后,沿平行金属板A、B中心线进入两板,A、B板间距为d、长度为L, A、B板间电压为U,屏CD足够大,距离A、B板右边缘2L,AB板的中心线过屏CD的中心且与屏CD垂直。试求电子束打在屏上的位置到屏中心间的距离。
自主训练
电子离开电场,就好象从中点沿直线离开的:
θ
对加速过程由动能定理:
分析与解答
13、质量为1×10-25kg、电量为1×10-16C的带电粒子以2×106m/s速度从水平放置的平行金属板A、B中央沿水平方向飞入板间,如图所示。已知板长L=10cm,间距d=2cm,当AB间电压在 范围内时,此带电粒子能从板间飞出。
自主训练
v0
+ + + + +
- - - - -
θ
对偏转过程由偏转角正切公式:
或对偏转过程由侧移公式:
分析与解答
14、初速度为2×107m/s的电子沿平行金属板间的中心线射入板中,板长为30cm,相距为4cm,在两板间加上如图所示的正弦交变电压。已知电子的质量为9×10-31Kg,电量为1.6×10-19C,不计电子重力,求:要使所有的电子都能离开电场,图中电压的最大值U0需满足什么条件?
自主训练
可认为在t时间内电场不变
设电子在两板间的运动时间为t
设电子在偏转电压为U0时进入板间
分析与解答
?带电粒子在交变电场中的运动
在两个相互平行的金属板间加交变电压时,在两板间便可获得交变电场。此类电场从空间看是匀强电场,即同一时刻,电场中各个位置处电场强度的大小、方向都相同;从时间上看是变化的,即电场强度的大小、方向都可随时间变化。
研究带电粒子在这种交变电场中的运动, 关键是根据电场变化的特点,正确地判断粒子的运动情况。
当带电粒子通过电场的时间远远小于电场变化的周期时,可认为电场强度的大小、方向都不变。
小 结
产生高速飞行的电子束
使电子沿x方向偏移
※四、示波器的原理
使电子沿y方向
偏移
示波器是一种用来观察电信号随时间变化的电子仪器。
核心部件:
由电子枪、偏转电极和荧光屏组成,管内抽成真空。
示波管
电子枪部分:
偏转电极部分:
荧光屏部分:
发射出电子
使电子沿两方向偏转
电子使荧光物质受激而发光
※四、示波器的原理
※思考与讨论:
电子将打在光屏上的哪一点?
试在图中标出来。
电子将打在光屏上的哪一点?
试在图中标出来。
如果信号电压是周期性的,并且扫描电压与信号电压周期相同,就可以在荧光屏上出现稳定的图象了。
※15、如图所示的示波管,如果在YY’之间加如图所示的交变电压,同时在XX’之间加如图所示的锯齿形电压,使X的电势比X’高,在荧光屏上会看到什么图形?
自主训练
※15、如图所示的示波管,如果在YY’之间加如图所示的交变电压,同时在XX’之间加如图所示的锯齿形电压,使X的电势比X’高,在荧光屏上会看到什么图形?
X
Y
O
0
※16、真空室中电极K发出电子(初速不计),经过电压为U1的加速电场后,由小孔S沿水平金属板A、B间的中心线射入板中,板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,已知电子的质量为m,带电量为e,不计电子重力,求:
(1)电子进入AB板时的初速度;?
(2)要使所有的电子都能离开AB板,图乙中电压的最大值U0需满足什么条件?
(3)在荧光屏上
会看到什么图形?
自主训练
设电子进入AB板时的初速度为v0
设电子在偏转电压为U0时进入AB板间
分析与解答
1、研究带电粒子在电场中运动的两条主要线索
(1)力和运动的关系——牛顿第二定律
根据带电粒子受到的电场力,用牛顿第二定律找出加速度,结合运动学公式确定带电粒子的速度、位移等.这条线索通常适用于恒力作用下做匀变速运动的情况.
(2)功和能的关系——动能定理
根据电场力对带电粒子所做的功,引起带电粒子的能量发生变化,利用动能定理或从全过程中能量的转化,研究带电粒子的速度变化,经历的位移等.这条线索同样也适用于不均匀的电场.
2、研究带电粒子在电场中运动的两类重要的思维技巧
(1)类比与等效
电场力和重力都是恒力,在电场力作用下的运动可与重力作用下的运动类比.例如,垂直射入平行板电场中的带电粒子的运动可类比于平抛,带电单摆在竖直方向匀强电场中的运动可等效于重力场强度g值的变化等.
(2)整体法(全过程法)
电荷间的相互作用是成对出现的,把电荷系统的整体作为研究对象,就可以不必考虑其间的相互作用.
电场力的功与重力的功一样,都只与始末位置有关,与路径无关.它们分别引起电荷电势能的变化和重力势能的变化,从电荷运动的全过程中功能关系出发(尤其从静止出发末速度为零的问题)往往能迅速找到解题入口或简化计算.
2、研究带电粒子在电场中运动的两类重要的思维技巧
