人教版八年级下册数学易错题专项训练 18.1 平行四边形测试题(含解析)
文档属性
| 名称 | 人教版八年级下册数学易错题专项训练 18.1 平行四边形测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:58:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版八年级下册易错题专题
18.1 平行四边形
一.选择题(共5小题)
1.如图,在平行四边形ABCD中,对角线AC和BD相交于O,∠BCD的平分线CE与边AB相交于E,若EB=EA=EC,那么下列结论正确的个数有( )
①∠ACE=30° ②OE∥DA ③S□ABCD=AC?AD ④CE⊥DB
A.1 B.2 C.3 D.4
2.如图,能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AB=CD B.∠A=∠B,∠C=∠D
C.∠A=∠C,∠B=∠D D.AB=AD,CB=CD
3.如图,□ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
A. B. C. D.
4.如图,EF过□ABCD对角线的交点O,交AD于点E,交BC于点F,若□ABCD的周长为20,OE=2,则四边形EFCD的周长为( )
A.15 B.14 C.13 D.12
5.如图,在平行四边形ABCD中,E,F分别是边AD,BC的中点,AC分别交BE,DF于G,H,试判断下列结论:①△ABE≌△CDF;②AG=GH=HC;③2EG=BG;④S△ABG:S四边形GHDE=2:3,其中正确的结论是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共3小题)
6.如图,在R△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为 .
7.在平面直角坐标系xOy中,已知点A(0,-2),点B(3m,2m+1),点C(6,2),点D.
(1)线段AC的中点E的坐标为 ;
(2)□ABCD的对角线BD长的最小值为 .
8.在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交□ABCD的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
(1)如图①,四边形EGFH的形状是 ;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,四边形EGFH的形状是 .
三.解答题(共7小题)
9.如图,设线段AB的中点为C,以AC和CB为对角线作平行四边形AECD、BFCG.又作平行四边形CFHD、CGKE.求证:H,C,K三点共线.
10.已知:如图,□ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
(1)求证:OE=OF;
(2)楚接BE,DF,求证:BE=DF.
11.如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10;
(1)求证:四边形ABCD是平行四边形.
(2)求四边形ABCD的面积.
12.如图,在平行四边形ABCD中,E,F分别为边AB、CD的中点,连结BD.
(1)求证:△ADE≌△CBF;
(2)若∠ADB=90°,则四边形BEDF是什么四边形?证明你的结论.
13.如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.
(1)若AH=3,HE=1,求△ABE的面积;
(2)若∠ACB=45°,求证:DF=CG.
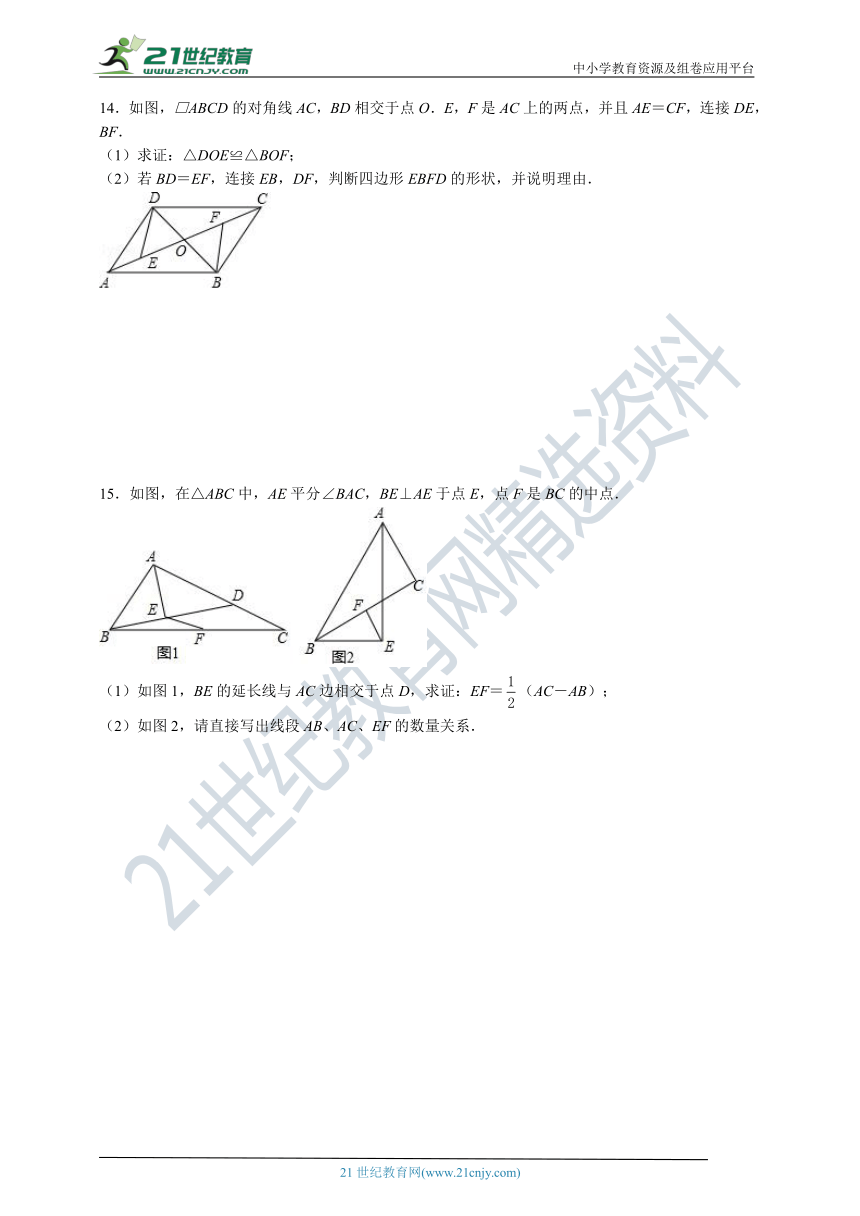
14.如图,□ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接EB,DF,判断四边形EBFD的形状,并说明理由.
15.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC-AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
参考答案
一.选择题
1.解:∵四边形ABCD是平行四边形,
∴AB∥CD,OD=DB,
∴∠DCA=∠CEB,
∵∠DCA=∠BCE,
∴∠BCE=∠CEB,
∴BC=EC,
∵EB=EA=EC,
∴∠ACB=90°,EC=BC=EB,
∴△BEC是等边三角形,
∴∠ABC=60°,
∴∠CAB=30°,故①正确,
∵OD=DB,AE=EB,
∴OE∥AD,故②正确,
∵AD∥BC,
∴∠DAC=∠ACB=90°,
∴AD⊥AC,
∴S□ABCD=AC?AD,故③正确,
假设CE⊥BD,则推出四边形ABCD是菱形,显然不可能,故④错误,
故选:C.
2.解:A、AD∥BC,AB=CD不能判定四边形ABCD是平行四边形,故此选项错误;
B、∠A=∠B,∠C=∠D不能判定四边形ABCD是平行四边形,故此选项错误;
C、∠A=∠C,∠B=∠D能判定四边形ABCD是平行四边形,故此选项正确;
D、AB=AD,CB=CD不能判定四边形ABCD是平行四边形,故此选项错误;
故选:C.
3.解:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵△ABO是等边三角形,
∴AO=BO=AB,
∴AO=OC=BO=OD,
∴AC=BD,
∴四边形ABCD是矩形.
∴OB=OC,∠ABC=90°,
∵△ABO是等边三角形,
∴∠ABO=60°,
∴∠OBC=∠OCB=30°,∠BOC=120°,
∵BO⊥OE,
∴∠BOE=90°,∠EOC=30°,
∴∠EOC=∠ECO,
∴EO=EC,
∴BE=2EO=2CE,
∵CD=1,
∴BC=CD=,
∴EC=BC=,
故选:D.
4.解:∵四边形ABCD是平行四边形,周长为20,
∴AB=CD,BC=AD,OA=OC,AD∥BC,
∴CD+AD=10,∠OAE=∠OCF,
在△AEO和△CFO中,
,
∴△AEO≌△CFO(ASA),
∴OE=OF=2,AE=CF,
则EFCD的周长=ED+CD+CF+EF=(DE+CF)+CD+EF=AD+CD+EF=10+4=14.
故选:B.
5.解:在□ABCD中,AB=CD,∠BAE=∠DCF,BC=DA;
E、F分别是边AD、BC的中点,
∴AE=CF,
∴△ABE≌△CDF,故①正确,
∵AD∥BC,
∴△AGE∽△BCG,△CHF∽△AHD,
∴AG:GC=EG:BG=AE:BC,CH:AH=CF:AD,
∵E,F分别是边AD,BC中点,
∴AE=AD,CF=BC,
∴AE:BC=1:2,CF:AD=1:2,
∴EG:BG=AG:CG=1:2,CH:AH=1:2,
∴AG=CH=AC,2EG=BG,故③正确;
∴AG=GH=CH,故②正确.
∵S△ABG=2S△AEG,S四边形GHDE=3S△AEG,
∴S△ABG:S四边形GHDE=2:3,故④正确.
故选:D.
二.填空题
6.答案:或.
【解答】解:取BC、AB的中点H、G,理解MH、HG、MG.
如图1中,当点C′落在MH上时,设NC=NC′=x,
由题意可知:MC=MC′=2,MH=,HC′=,HN=-x,
在Rt△HNC中,∵HN2=HC′2+NC′2,
∴(-x)2=x2+()2,
解得x=.
如图2中,当点C′落在GH上时,设NC=NC′=x,
在Rt△GMC′中,MG=CH=,MC=MC′=2,
∴GC′=,
∵△HNC′∽△GC′M,
∴,
∴=,
∴x=.
如图3中,当点C′落在直线GM上时,易证四边形MCNC′是正方形,可得CN=CM=2.
此时点C′在中位线GM的延长线上,不符合题意舍弃.
综上所述,满足条件的线段CN的长为或.
故答案为为或.
7.答案:
(1)(3,0);
(2).
【解答】解:(1)∵点A(0,-2),点C(6,2),
∴线段AC的中点E的坐标为(3,0)
故答案为(3,0).
(2)解:如图,∵点B(3m,2m+1),
∴令 ,
∴y=x+1,
∴B在直线y=x+1上,
∴当BD⊥直线y=x+1时,BD最小,
过B作BH⊥x轴于H,则BH=2m+1,
∵BE在直线y=x+1上,且点E在x轴上,
∴E(-,0),G(0,1),
∵平行四边形对角线交于一点,且AC的中点一定在x轴上,
∴F是AC的中点,
∵A(0,-2),点C(6,2),
∴F(3,0).
在Rt△BEF中,∵BH2=EH?FH,
∴(2m+1)2=(3m+)(3-3m),
解得:m=或-(舍弃),
∴B(,),
∴BF==
∴BD=2BF=,
则对角线BD的最小值是;
故答案为.
8.答案:
(1)平行四边形;
(2)菱形;
(3)菱形;
(4)正方形;
【解答】解:(1)结论:四边形EGFH是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,AE∥CF,
∴∠AEO=∠CFO,∵∠AOE=∠COF,
∴△AOE≌△COF,
∴OE=OF,同理可证:OG=OH,
∴四边形EGFH是平行四边形,
(2)∵四边形EGFH是平行四边形,EF⊥GH,
∴四边形EGFH是菱形;
(3)菱形;
由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
(4)四边形EGFH是正方形;
证明:∵AC=BD,
∴□ABCD是矩形;
又∵AC⊥BD,
∴□ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.
故答案为:平行四边形,菱形,菱形,正方形;
三.解答题
9.证明:如图,连接DE交AC于N,连接EG交KC于M,连接DF交CH于Q,连接FG交BC于J,连接MN,NQ,QJ,JM,DG.
∵四边形AECD是平行四边形,
∴EN=ND,同法可证:EM=MG,
∴MN∥DG,MN=DG,
同法可证:QJ∥DG,QJ=DG,
∴MN∥QJ,MN=QJ,
∴四边形MNQJ是平行四边形,
∴NJ与MQ互相平分,
∵AC=BC,AN=CN,CJ=BJ,
∴M、C、Q共线,
∴H,C,K三点共线.
10.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠OAF=∠OCE,
在△OAF和△OCE中,
,
∴△AOF≌△COE(ASA),
∴OE=OF;
(2)证明:∵四边形ABCD是平行四边形,
∴OB=OD,∵OE=OF,
∴四边形DEBF是平行四边形,
∴BE=DF.
11.(1)证明∵∠DBC=90°,BE=3,BC=4,
∴BC===5,
又∵AE=AC-CE,且AC=10
∴AE=10-5=5
∴AE=EC,又DE=EB
∴四边形ABCD是平行四边形
(2)解:S平行四边形ABCD=BC?BD=4×6=24.
12.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,DC=AB,
∵E,F分别为边AB、CD的中点,
∴DF=CF=DC,AE=BE=AB,
∴AE=CF,
在△ADE和△CBF中,
∴△ADE≌△CBF(SAS);
(2)菱形,
证明:∵边形ABCD是平行四边形,
∴DC=AB,CD∥AB,
∴DF∥EB,
∵E,F分别为边AB、CD的中点,
∴DF=CF=DC,AE=BE=AB,
∴DF=EB,
∴四边形DEBF是平行四边形,
∵∠ADB=90°,
∴DE=AB,
∴DE=EB,
∴四边形DEBF是菱形.
13.解:(1)∵AH=3,HE=1,
∴AB=AE=4,
又∵Rt△ABH中,BH==,
∴S△ABE=AE×BH=×4×=2;
(2)如图,过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,
则∠AMB=∠AME=∠BNG=90°,
∵∠ACB=45°,
∴∠MAC=∠NGC=45°,
∵AB=AE,
∴BM=EM=BE,∠BAM=∠EAM,
又∵AE⊥BG,
∴∠AHK=90°=∠BMK,而∠AKH=∠BKM,
∴∠MAE=∠NBG,
设∠BAM=∠MAE=∠NBG=α,则∠BAG=45°+α,∠BGA=∠GCN+∠GBC=45°+α,
∴AB=BG,
∴AE=BG,
在△AME和△BNG中,
,
∴△AME≌△BNG(AAS),
∴ME=NG,
在等腰Rt△CNG中,NG=NC,
∴GC=NG=ME=BE,
∴BE=GC,
∵O是AC的中点,
∴OA=OC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠OAF=∠OCE,∠AFO=∠CEO,
∴△AFO≌△CEO(AAS),
∴AF=CE,
∴AD-AF=BC-EC,即DF=BE,
∴DF=BE=CG.
14.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
在△DEO和△BOF中,
∴△DOE≌△BOF.
(2)解:结论:四边形EBFD是矩形.
理由:∵OD=OB,OE=OF,
∴四边形EBFD是平行四边形,
∵BD=EF,
∴四边形EBFD是矩形.
15.(1)证明:如图1中,
∵AE⊥BD,
∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°,
∵∠BAE=∠DAE,
∴∠ABE=∠ADE,
∴AB=AD,∵AE⊥BD,
∴BE=DE,∵BF=FC,
∴EF=DC=(AC-AD)=(AC-AB).
(2)结论:EF=(AB-AC),
理由:如图2中,延长AC交BE的延长线于P.
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP,∵AE⊥BD,
∴BE=PE,∵BF=FC,
∴EF=PC=(AP-AC)=(AB-AC).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
