人教版八年级下册数学课件:19.2.3一次函数与方程、不等式(共23张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:19.2.3一次函数与方程、不等式(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 19:44:18 | ||
图片预览




文档简介
(共23张PPT)
19.2.3一次函数与方程、不等式
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解方程2x+20=0
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
(2) 当y=0时 ,即
从“函数值”
角度看
两个问题实际上是同一个问题.
1、根据下列图像,你能说出哪些一元一次 方程的解?并直接写出相应方程的解?
5x=0的解
其解为X=0
3x+6=0的解
其解为X=2
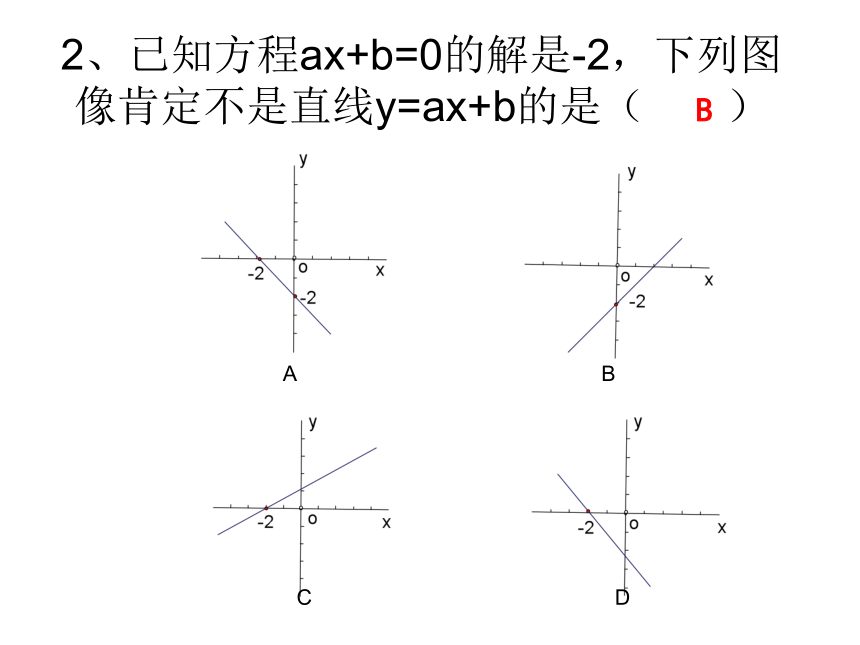
2、已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
B
C
D
B
3.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是______
4
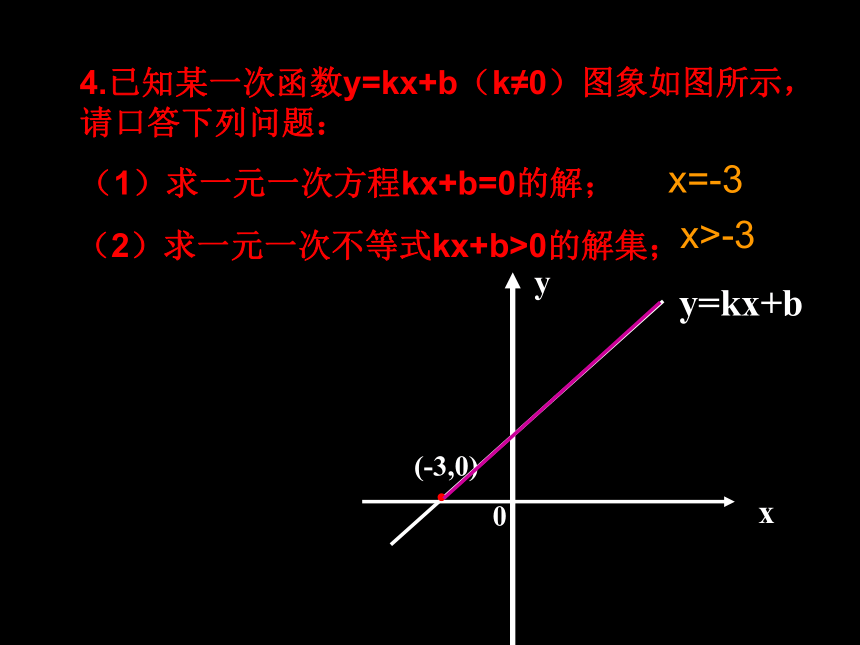
4.已知某一次函数y=kx+b(k≠0)图象如图所示,请口答下列问题:
(1)求一元一次方程kx+b=0的解;
(2)求一元一次不等式kx+b>0的解集;
x=-3
x>-3
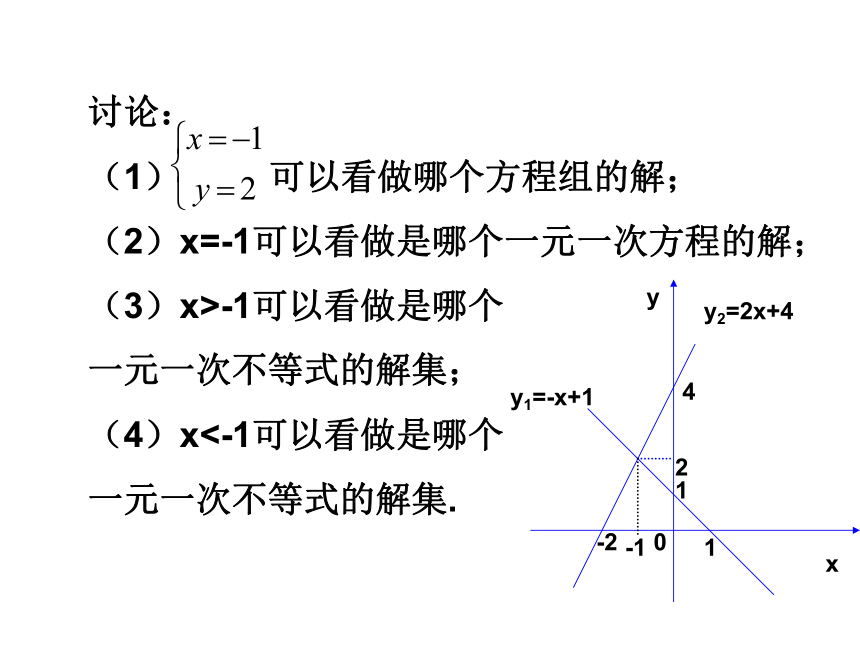
讨论:
(1) 可以看做哪个方程组的解;
(2)x=-1可以看做是哪个一元一次方程的解;
(3)x>-1可以看做是哪个
一元一次不等式的解集;
(4)x<-1可以看做是哪个
一元一次不等式的解集.
基础练习,提高能力
(4,0)
x>4
x<4
x>6
4y=2
y=-1
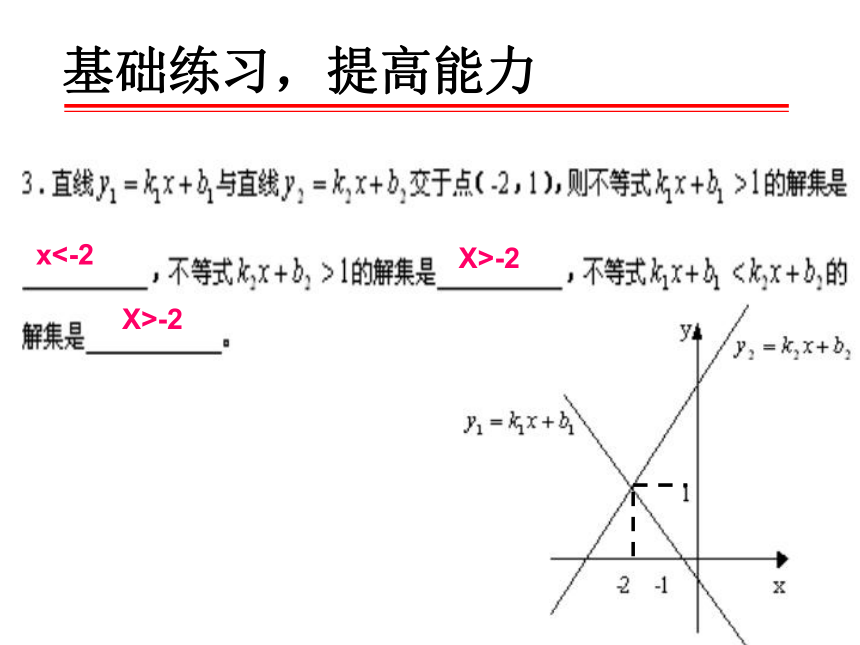
基础练习,提高能力
x<-2
X>-2
X>-2
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了某公司产品的销售收入与销售量的关系,根据图意填空:
L1
当销售量为2吨时,销售收入= 元,
2000
销售收入
练一练
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
当销售成本=4500元时,销售量= 吨;
5
l2 反映了该公司产品的销售成本与销售量的关系, 根据图意填空:
销售成本
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了公司产品的销售收入与销售量的关系。
l1对应的函数表达式是 ,
y=1000x
(4,4000)
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2 反映了公司产品的销售成本与销售量的关系。
l2对应的函数表达式是 。
y=500x+2000
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
L1
销售收入
l1 反映了公司产品的销售收入与销售量的关系。
l2 反映了公司产品的销售成本与销售量的关系。
l1
l2
(1)当销售量为6吨时,销售收入= 元,
销售成本= 元, 利润= 元。
6000
5000
(2)当销售量为 时,销售收入等于销售成本。
4吨
销售收入
销售成本
1000
销售收入和销售成本都是4000元
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(3)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);
大于4吨
小于4吨
销售收入
销售成本
5
6
1
2
3
P
7
8
一艘轮船以20km/h的速度从甲港驶160km远的乙港,2h后,一艘快艇以40km/h的速度也从甲港驶往乙港。设轮船行驶的时间为xkm,分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式,并在直角坐标系中画出函数的图象,观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60km?哪一艘船先驶过100km?
o
y
x
1 2 3 4 5 6 7 8
20
40
60
80
100
y1=20x
y2=40(x-2)
观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60km?哪一艘船先驶过100km?
某长途汽车客运公司规定旅客可随身携带一定质量的行李。如果超过规定质量,那么需要购买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。根据图象回答下列问题;
(1)求y与x之间的函数关系式;
(2)求旅客最多可免费携带行李的质量;
(3)某旅客所买的行李票的费用为4≤x≤15元,求他所带行李的质量的范围。
一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.如果所挂物体的质量为x㎏,弹簧的长度是ycm。
(1)求弹簧长度为25cm时,所挂物体的质量。
(2)求弹簧所挂物体的最大质量是多少?
x
小结
一次函数y=kx+b(k≠0)
y>0(<0)
一元一次不等式kx+b>0(<0)
(k≠0)
一元一次方程kx+b=0 (k≠0)
y=0
19.2.3一次函数与方程、不等式
(快速回答:只选一个做,做完后和前后座交流,也可以两个都做)
(1)解方程2x+20=0
(2)当自变量x为何值时,函数y=2x+20的值为0?
解:(1) 2x+20=0
(2) 当y=0时 ,即
从“函数值”
角度看
两个问题实际上是同一个问题.
1、根据下列图像,你能说出哪些一元一次 方程的解?并直接写出相应方程的解?
5x=0的解
其解为X=0
3x+6=0的解
其解为X=2
2、已知方程ax+b=0的解是-2,下列图像肯定不是直线y=ax+b的是( )
A
B
C
D
B
3.直线y=3x+6与x轴的交点的横坐标x的值是方程2x+a=0的解,则a的值是______
4
4.已知某一次函数y=kx+b(k≠0)图象如图所示,请口答下列问题:
(1)求一元一次方程kx+b=0的解;
(2)求一元一次不等式kx+b>0的解集;
x=-3
x>-3
讨论:
(1) 可以看做哪个方程组的解;
(2)x=-1可以看做是哪个一元一次方程的解;
(3)x>-1可以看做是哪个
一元一次不等式的解集;
(4)x<-1可以看做是哪个
一元一次不等式的解集.
基础练习,提高能力
(4,0)
x>4
x<4
x>6
4
y=-1
基础练习,提高能力
x<-2
X>-2
X>-2
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了某公司产品的销售收入与销售量的关系,根据图意填空:
L1
当销售量为2吨时,销售收入= 元,
2000
销售收入
练一练
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
当销售成本=4500元时,销售量= 吨;
5
l2 反映了该公司产品的销售成本与销售量的关系, 根据图意填空:
销售成本
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1 反映了公司产品的销售收入与销售量的关系。
l1对应的函数表达式是 ,
y=1000x
(4,4000)
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l2 反映了公司产品的销售成本与销售量的关系。
l2对应的函数表达式是 。
y=500x+2000
x/吨
y/元
O
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
L1
销售收入
l1 反映了公司产品的销售收入与销售量的关系。
l2 反映了公司产品的销售成本与销售量的关系。
l1
l2
(1)当销售量为6吨时,销售收入= 元,
销售成本= 元, 利润= 元。
6000
5000
(2)当销售量为 时,销售收入等于销售成本。
4吨
销售收入
销售成本
1000
销售收入和销售成本都是4000元
1
2
3
4
5
6
1000
4000
5000
2000
3000
6000
l1
l2
(3)当销售量 时,该公司赢利(收入大于成本);
当销售量 时,该公司亏损(收入小于成本);
大于4吨
小于4吨
销售收入
销售成本
5
6
1
2
3
P
7
8
一艘轮船以20km/h的速度从甲港驶160km远的乙港,2h后,一艘快艇以40km/h的速度也从甲港驶往乙港。设轮船行驶的时间为xkm,分别列出轮船和快艇行驶的路程y km与时间x h的函数关系式,并在直角坐标系中画出函数的图象,观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60km?哪一艘船先驶过100km?
o
y
x
1 2 3 4 5 6 7 8
20
40
60
80
100
y1=20x
y2=40(x-2)
观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60km?哪一艘船先驶过100km?
某长途汽车客运公司规定旅客可随身携带一定质量的行李。如果超过规定质量,那么需要购买行李票,行李票费用y(元)是行李质量x(kg)的一次函数。根据图象回答下列问题;
(1)求y与x之间的函数关系式;
(2)求旅客最多可免费携带行李的质量;
(3)某旅客所买的行李票的费用为4≤x≤15元,求他所带行李的质量的范围。
一根长20cm的弹簧,一端固定,另一端挂物体。在弹簧伸长后的长度不超过30cm的限度内,每挂1㎏质量的物体,弹簧伸长0.5cm.如果所挂物体的质量为x㎏,弹簧的长度是ycm。
(1)求弹簧长度为25cm时,所挂物体的质量。
(2)求弹簧所挂物体的最大质量是多少?
x
小结
一次函数y=kx+b(k≠0)
y>0(<0)
一元一次不等式kx+b>0(<0)
(k≠0)
一元一次方程kx+b=0 (k≠0)
y=0
