数学人教版六年级下6.3整理和复习课件(41张ppt)
文档属性
| 名称 | 数学人教版六年级下6.3整理和复习课件(41张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-09 00:00:00 | ||
图片预览






文档简介
课件41张PPT。6.3 统计与概率
人教版六年级数学下册整理和复习6.4 数学思考学习目标进一步明确统计的意义,熟练掌握整理数据、编制统计表的方法,学会进行简单的统计。
理性的掌握各种统计图的特点,进一步认识、掌握各种统计图的不同特征及适用范围。
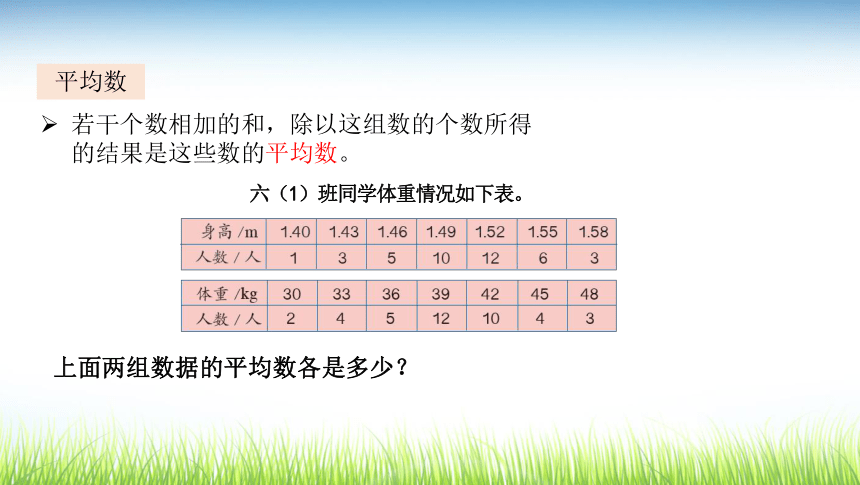
进一步理解平均数、中位数、众数这三种统计量的实际意义。
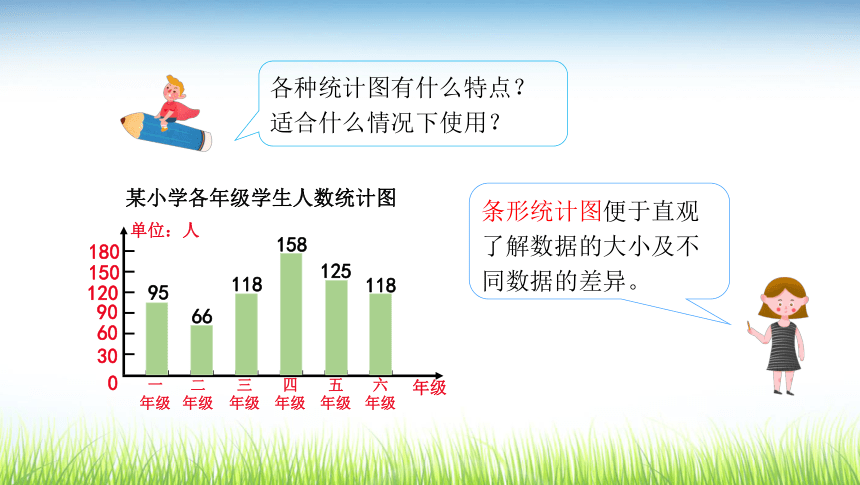
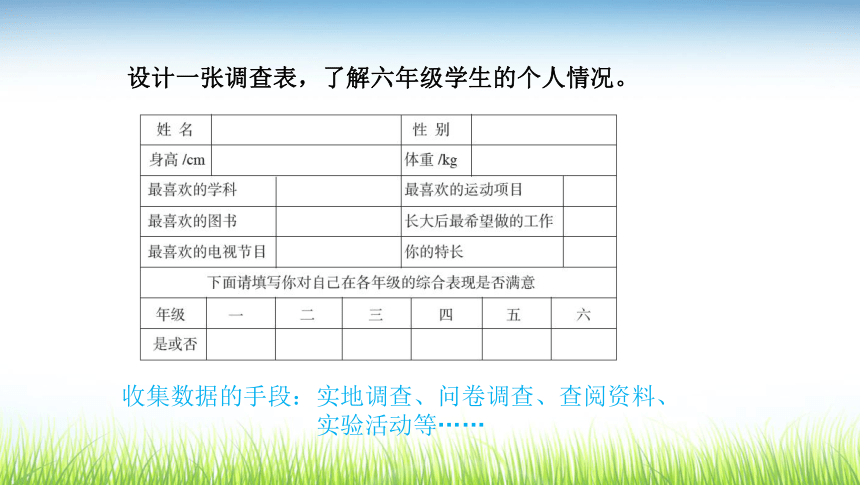
回顾事件发生具有确定性和不确定性,不确定性中又有可能性大小不等和可能性大小相等两种情况。回顾复习我们学过哪些统计与可能性的知识?我们学过统计表,还有平均数。我们还学过条形统计图、折线统计图、扇形统计图。还知道事件发生的可能性有大有小,还有不可能发生的事件。各种统计图有什么特点?适合什么情况下使用?条形统计图便于直观了解数据的大小及不同数据的差异。各种统计图有什么特点?适合什么情况下使用?折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化的情况。各种统计图有什么特点?适合什么情况下使用?扇形统计图可以直观地表示出部分占整体的百分比。设计一张调查表,了解六年级学生的个人情况。收集数据的手段:实地调查、问卷调查、查阅资料、
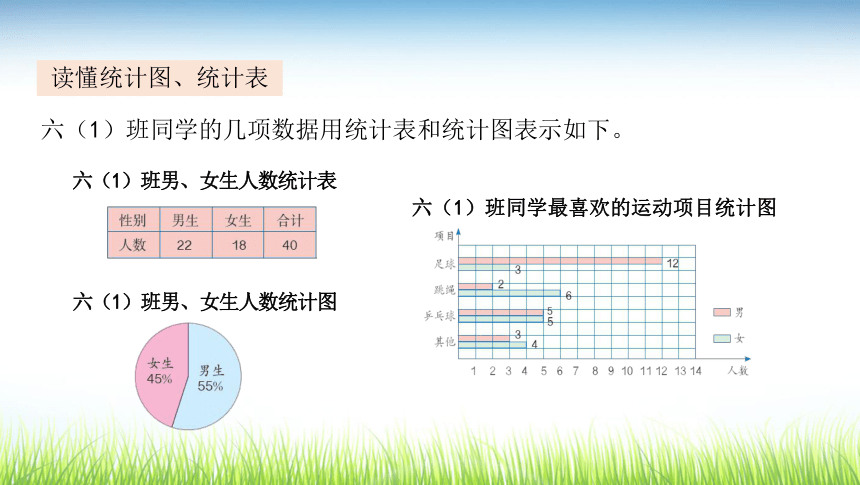
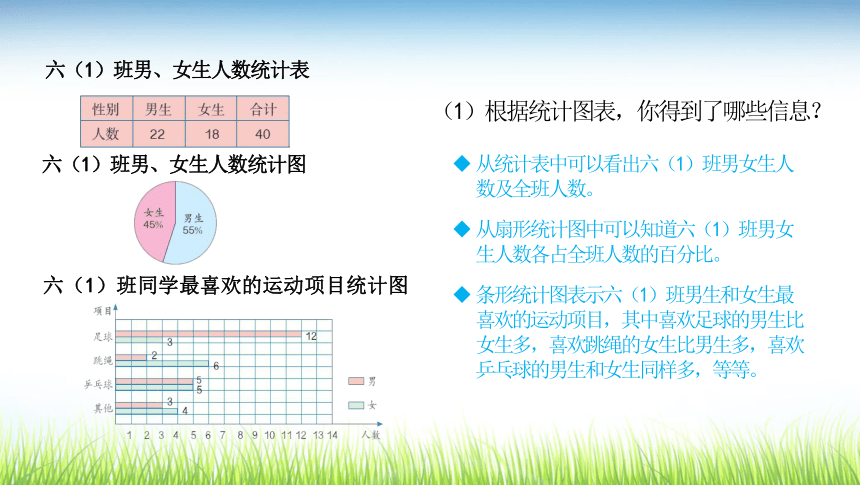
实验活动等……读懂统计图、统计表六(1)班同学的几项数据用统计表和统计图表示如下。(1)根据统计图表,你得到了哪些信息?从统计表中可以看出六(1)班男女生人数及全班人数。
从扇形统计图中可以知道六(1)班男女生人数各占全班人数的百分比。
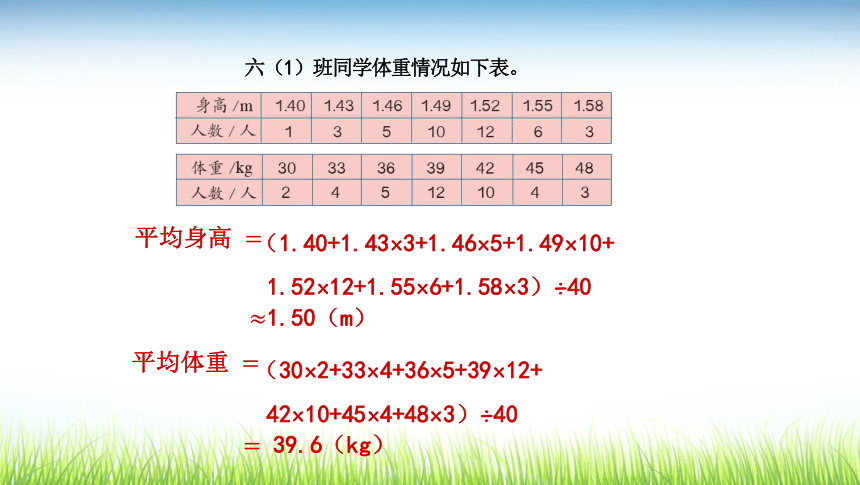
条形统计图表示六(1)班男生和女生最喜欢的运动项目,其中喜欢足球的男生比女生多,喜欢跳绳的女生比男生多,喜欢乒乓球的男生和女生同样多,等等。上面两组数据的平均数各是多少?若干个数相加的和,除以这组数的个数所得的结果是这些数的平均数。平均数什么数据能代表全班同学的身高和体重?1.52 m能代表全班同学的身高;
39.6 kg能代表全班同学的体重。如果把全班同学编号,随意抽取一名学生,该生体重在36 kg及以下的可能性大?还是在39 kg及以上的可能性大?为什么?39kg及以上的可能性大39kg及以上的人数:12+10+4+3=29(人)
36kg及以下的人数: 2+4+5=11(人)随堂小测1.将正确答案的序号填在括号里。
A.条形 B.折线 C.扇形(1)要反映各年级人数占全校学生的多少,用( )统计图比较合适。
(2)记录病人住院期间体温的变化情况,用( )统计图比较合适。
(3)要反映各车间的工人数量,用( )统计图比较合适。CBA2. 小明在期中考试中,语、数、外三门功课的平均分数是93分,
数学得了95分,语文和外语的得分相同,语文得了( )分。3. 某公司销售部有15人,销售部为了制定月销售额,统计了这
15人上月的销售额,如下表。??这组数据的平均数是多少?(1800+510+250×3+210×5+150×3+120×2)÷15=3204. 连线4.下图是某自行车厂去年下半年自行车产量和销售量的情况。(1)哪几个月的产量小于销量?9 ̄12月的产量小于销量。(2)你还能提出什么问题?并解答。问题:去年下半年生产的自行车
比销售的少多少? 166-162.6=3.4(万台)
答:去年下半年生产的自行车
比销售的少3.4万台。5.下面是实验小学六年级参加学校兴趣小组情况统计图。(1)六年级共有学生多少人?36÷(1-20%-28%-34%)=200(人)(2)体育组的人数比音乐组多百分之几?(34%×200-28%×200)÷(28%×200)≈21.4%课后作业1.从课后习题中选取;
2.完成练习册本课时的习题。6.3 统计与概率
人教版六年级数学下册整理和复习6.4 数学思考学习目标掌握根据图形或数列找规律的方法。
会解决逻辑推理中的排列组合的问题。
用列表法解决语言逻辑判断的问题。
学会用演绎推理的思想解决问题。
会利用等式的性质进行等量代换。
使学生进一步体会数形结合思想,感受数学的魅力,增强数学学习兴趣。回顾复习同学们,课前我们来做一个游戏吧,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段? 别着急,从2个点开始,逐渐增加点数,找找规律。太乱了,我都数昏了。5+4+3+2+1=15(条)按顺序画,不重复,
不遗漏。8个点连成的线段怎么数呢?有没有什么规律?仔细观察表格,找规律。2132343654106515………………规律如下表格:8个点连成线段的条数:1+2+3+4+5+6+7=28(条)每次增加的线段条数比点数少1。观察“点数”和“增加条数”,你发现了什么规律?每次增加的线段条数比点数少1。根据规律,你知道12个点、20个点能连多少条线段吗?1+2+3+4+5+6+7+8+9+10+11=66(条)—12个点=190(条) —20个点1+2+3+4+5+6+……+18+19???六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?知道的信息:
第一次到会的有A,B,C,说明A,B,C三位班长不同班。
第二次到会的有B,D,F,说明三位班长不同班。
第三次到会的有A,E,F,说明三位班长不同班。这个问题太复杂了。用数字“1” 表示到会,用数字“0”表示没到会。用列表的方法试一试。010110100011第一次:A只可能和D、E、F同班。1√√√√√01√第二次:A只可能和D、E同班。第三次:A只可能和D同班。继续推理,B、C可能和谁是同班呢?1√√√1A和D同班,则B只可能和E、F同班。根据第二轮推测,B和F同班。据此可推出C、E同班。等量代换=18圈起来的这一步运用了什么数学思想?如右图,两条直线相交于点O。∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?(2)你能推出∠1=∠3吗? 随堂小测1.观察下图,想一想。每幅图棋子数有什么规律?1 4 9 161×1每行的棋子数×行数=棋子总数2×23×34×4 (1)第7幅图有多少个棋子?第15幅图呢?每行的棋子数×行数=棋子总数7×7=49(个) 15×15=225(个)(2)每边的棋子数与图形的序号有什么关系?相等???每行的棋子数×行数=棋子总数2.王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。
王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?√×√×√√×××××3.求图形代表的数。
(1)○+△=150 ○= 4×△
○=( ) △=( )
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )1203061425课后作业1.从课后习题中选取;
2.完成练习册本课时的习题。
人教版六年级数学下册整理和复习6.4 数学思考学习目标进一步明确统计的意义,熟练掌握整理数据、编制统计表的方法,学会进行简单的统计。
理性的掌握各种统计图的特点,进一步认识、掌握各种统计图的不同特征及适用范围。
进一步理解平均数、中位数、众数这三种统计量的实际意义。
回顾事件发生具有确定性和不确定性,不确定性中又有可能性大小不等和可能性大小相等两种情况。回顾复习我们学过哪些统计与可能性的知识?我们学过统计表,还有平均数。我们还学过条形统计图、折线统计图、扇形统计图。还知道事件发生的可能性有大有小,还有不可能发生的事件。各种统计图有什么特点?适合什么情况下使用?条形统计图便于直观了解数据的大小及不同数据的差异。各种统计图有什么特点?适合什么情况下使用?折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化的情况。各种统计图有什么特点?适合什么情况下使用?扇形统计图可以直观地表示出部分占整体的百分比。设计一张调查表,了解六年级学生的个人情况。收集数据的手段:实地调查、问卷调查、查阅资料、
实验活动等……读懂统计图、统计表六(1)班同学的几项数据用统计表和统计图表示如下。(1)根据统计图表,你得到了哪些信息?从统计表中可以看出六(1)班男女生人数及全班人数。
从扇形统计图中可以知道六(1)班男女生人数各占全班人数的百分比。
条形统计图表示六(1)班男生和女生最喜欢的运动项目,其中喜欢足球的男生比女生多,喜欢跳绳的女生比男生多,喜欢乒乓球的男生和女生同样多,等等。上面两组数据的平均数各是多少?若干个数相加的和,除以这组数的个数所得的结果是这些数的平均数。平均数什么数据能代表全班同学的身高和体重?1.52 m能代表全班同学的身高;
39.6 kg能代表全班同学的体重。如果把全班同学编号,随意抽取一名学生,该生体重在36 kg及以下的可能性大?还是在39 kg及以上的可能性大?为什么?39kg及以上的可能性大39kg及以上的人数:12+10+4+3=29(人)
36kg及以下的人数: 2+4+5=11(人)随堂小测1.将正确答案的序号填在括号里。
A.条形 B.折线 C.扇形(1)要反映各年级人数占全校学生的多少,用( )统计图比较合适。
(2)记录病人住院期间体温的变化情况,用( )统计图比较合适。
(3)要反映各车间的工人数量,用( )统计图比较合适。CBA2. 小明在期中考试中,语、数、外三门功课的平均分数是93分,
数学得了95分,语文和外语的得分相同,语文得了( )分。3. 某公司销售部有15人,销售部为了制定月销售额,统计了这
15人上月的销售额,如下表。??这组数据的平均数是多少?(1800+510+250×3+210×5+150×3+120×2)÷15=3204. 连线4.下图是某自行车厂去年下半年自行车产量和销售量的情况。(1)哪几个月的产量小于销量?9 ̄12月的产量小于销量。(2)你还能提出什么问题?并解答。问题:去年下半年生产的自行车
比销售的少多少? 166-162.6=3.4(万台)
答:去年下半年生产的自行车
比销售的少3.4万台。5.下面是实验小学六年级参加学校兴趣小组情况统计图。(1)六年级共有学生多少人?36÷(1-20%-28%-34%)=200(人)(2)体育组的人数比音乐组多百分之几?(34%×200-28%×200)÷(28%×200)≈21.4%课后作业1.从课后习题中选取;
2.完成练习册本课时的习题。6.3 统计与概率
人教版六年级数学下册整理和复习6.4 数学思考学习目标掌握根据图形或数列找规律的方法。
会解决逻辑推理中的排列组合的问题。
用列表法解决语言逻辑判断的问题。
学会用演绎推理的思想解决问题。
会利用等式的性质进行等量代换。
使学生进一步体会数形结合思想,感受数学的魅力,增强数学学习兴趣。回顾复习同学们,课前我们来做一个游戏吧,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段? 别着急,从2个点开始,逐渐增加点数,找找规律。太乱了,我都数昏了。5+4+3+2+1=15(条)按顺序画,不重复,
不遗漏。8个点连成的线段怎么数呢?有没有什么规律?仔细观察表格,找规律。2132343654106515………………规律如下表格:8个点连成线段的条数:1+2+3+4+5+6+7=28(条)每次增加的线段条数比点数少1。观察“点数”和“增加条数”,你发现了什么规律?每次增加的线段条数比点数少1。根据规律,你知道12个点、20个点能连多少条线段吗?1+2+3+4+5+6+7+8+9+10+11=66(条)—12个点=190(条) —20个点1+2+3+4+5+6+……+18+19???六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?知道的信息:
第一次到会的有A,B,C,说明A,B,C三位班长不同班。
第二次到会的有B,D,F,说明三位班长不同班。
第三次到会的有A,E,F,说明三位班长不同班。这个问题太复杂了。用数字“1” 表示到会,用数字“0”表示没到会。用列表的方法试一试。010110100011第一次:A只可能和D、E、F同班。1√√√√√01√第二次:A只可能和D、E同班。第三次:A只可能和D同班。继续推理,B、C可能和谁是同班呢?1√√√1A和D同班,则B只可能和E、F同班。根据第二轮推测,B和F同班。据此可推出C、E同班。等量代换=18圈起来的这一步运用了什么数学思想?如右图,两条直线相交于点O。∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。(1)每相邻两个角可以组成一个平角,
一共能组成几个平角?(2)你能推出∠1=∠3吗? 随堂小测1.观察下图,想一想。每幅图棋子数有什么规律?1 4 9 161×1每行的棋子数×行数=棋子总数2×23×34×4 (1)第7幅图有多少个棋子?第15幅图呢?每行的棋子数×行数=棋子总数7×7=49(个) 15×15=225(个)(2)每边的棋子数与图形的序号有什么关系?相等???每行的棋子数×行数=棋子总数2.王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。
王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?√×√×√√×××××3.求图形代表的数。
(1)○+△=150 ○= 4×△
○=( ) △=( )
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )1203061425课后作业1.从课后习题中选取;
2.完成练习册本课时的习题。
