人教版高一物理必修二第六章 万有引力与航天总结(共16张PPT)
文档属性
| 名称 | 人教版高一物理必修二第六章 万有引力与航天总结(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 285.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-09 22:42:03 | ||
图片预览




文档简介
(共16张PPT)
第六章 万有引力与航天
总结
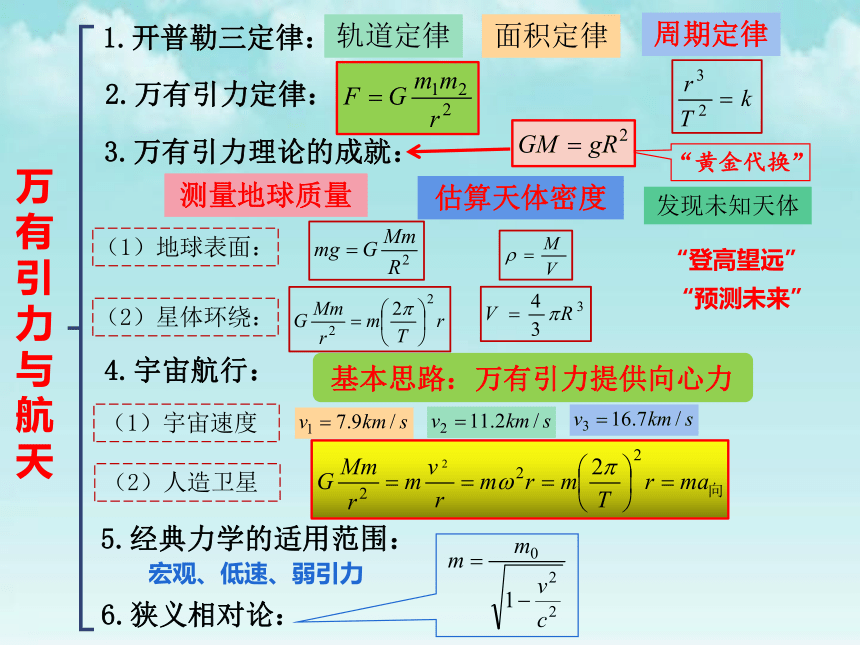
万有引力与航天
1.开普勒三定律:
轨道定律
面积定律
周期定律
2.万有引力定律:
3.万有引力理论的成就:
测量地球质量
估算天体密度
“登高望远”
4.宇宙航行:
(1)宇宙速度
(2)人造卫星
5.经典力学的适用范围:
宏观、低速、弱引力
6.狭义相对论:
(1)地球表面:
(2)星体环绕:
发现未知天体
基本思路:万有引力提供向心力
“黄金代换”
“预测未来”
规律总结
一、天体质量和密度的求解方法:
(1)自立更生法:
利用天体表面的重力加速度g和天体的半径R:
利用卫星绕天体做匀速圆周运动的半径r和周期T.
①
③若卫星在天体表面附近运行时,可认为轨道半径r等于
天体半径R,则天体密度
②若已知天体的半径R,
只要测出卫星环绕天体表面运行的周期T,就可估算中心天体的密度。
(2)借助外援法:
典例1:(2019安徽合肥质检)已知地球和月球的半径之比为4:1,其表面重力加速度之比为6:1,则地球和月球的密度之比为( )
A.2:3, B.3:2, C.4:1, D.6:1
所以地球和月球的密度之比为:
B
解析:
在星球表面的物体,重力和万有引力相等,
解得质量为:
则密度为:
典例1
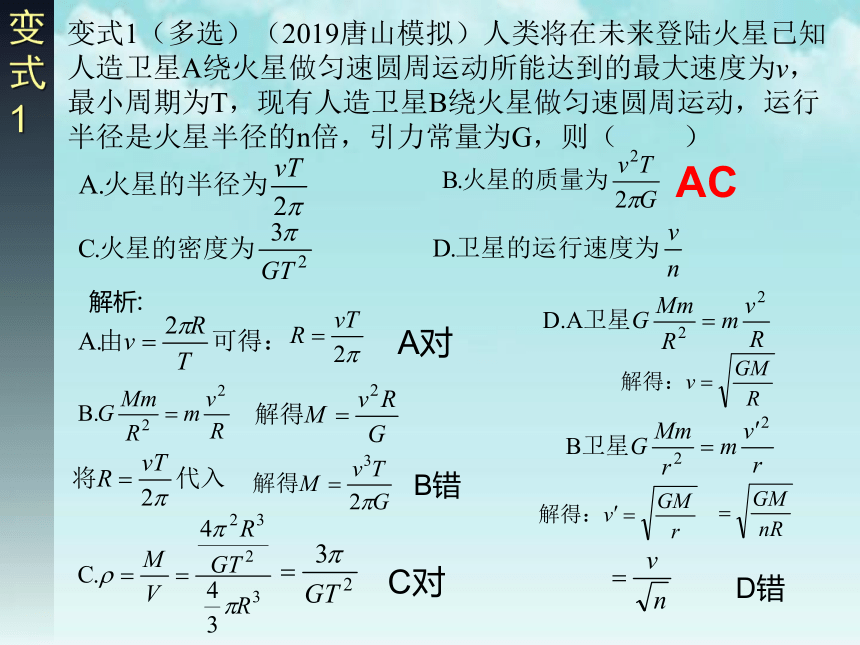
变式1(多选)(2019唐山模拟)人类将在未来登陆火星已知人造卫星A绕火星做匀速圆周运动所能达到的最大速度为v,最小周期为T,现有人造卫星B绕火星做匀速圆周运动,运行半径是火星半径的n倍,引力常量为G,则( )
B错
A对
解析:
AC
变式1
C对
D错
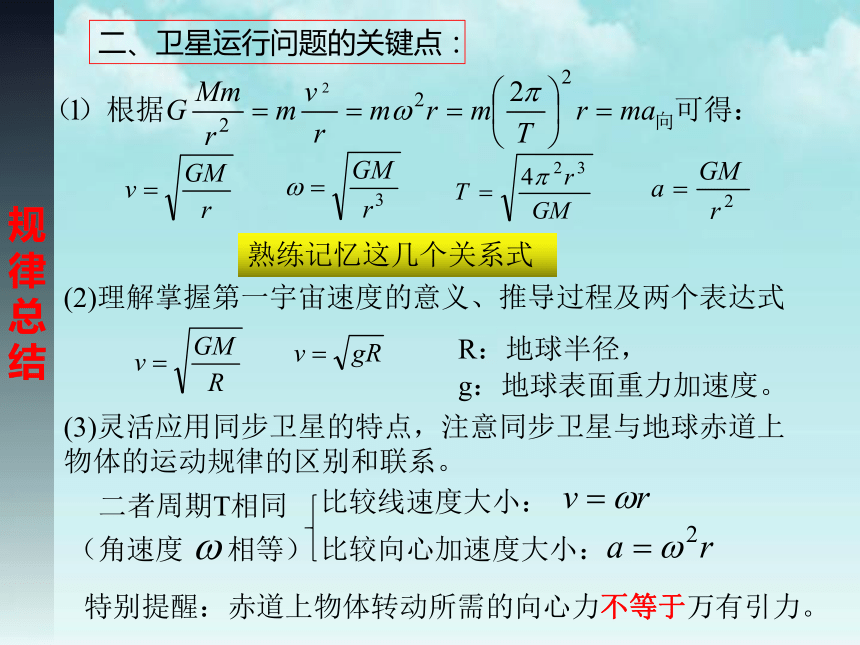
二、卫星运行问题的关键点:
(2)理解掌握第一宇宙速度的意义、推导过程及两个表达式
(3)灵活应用同步卫星的特点,注意同步卫星与地球赤道上物体的运动规律的区别和联系。
熟练记忆这几个关系式
R:地球半径,
g:地球表面重力加速度。
规律总结
特别提醒:赤道上物体转动所需的向心力不等于万有引力。
比较线速度大小:
比较向心加速度大小:
二者周期T相同
(角速度 相等)
典例2:2018年12月27日,“北斗三号”基本系统已完成建设,开始提供全球服务,其导航系统中部分卫星运行轨道如图所示,a为极地卫星,b为地球同步卫星,c为倾斜轨道卫星,其轨道平面与赤道平面有一定的夹角,周期与地球自转周期相同,下列说法正确的是( )
A.卫星a的线速度比卫星c的线速度小
B.卫星b的向心加速度比卫星c的向心加速度大
C.卫星b和卫星c的线速度大小相等
D.卫星a的机械能一定比卫星b的机械能大
a
c
b
解:
A不正确
B不正确
C.由A中的表达式可知:C正确
D.由于不知道卫星的质量关系,
D不正确
卫星a的机械能和卫星b的机械能的关系,
C
典例2
故无法判断
变式2.同步卫星与地心的距离为r,运行速率为v1向心加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是( )
a1
a2
a2
v2
v1
同步卫星
D
比较同步卫星、近地卫星和赤道上物体的线速度,角速度,周期和向心加速度的大小。
课后练习:
解析:
变式2
三、卫星变轨问题
1.发射(离心运动):卫星在轨道Ⅰ上的Q点加速进入Ⅱ轨道,在Ⅱ轨道上的P点加速进入Ⅲ轨道。
2.回收(近心运动):卫星在轨道Ⅲ上的P点减速进入Ⅱ轨道,在Ⅱ轨道上的Q点减速进入Ⅰ轨道。
vQ2 vQ1,
>
vP3 vP2
>
aQ2 = aQ1,
aP3 = aP2
月球
Ⅰ
Ⅱ
Ⅲ
P
Q
3.Ⅰ、Ⅱ轨道上Q点,Ⅱ、Ⅲ轨道上P点的速度和加速度的大小关系。
规律总结
典例3(2019河南郑州预测)“嫦娥四号”探测器成功发射,之后实施近月制动,顺利完成“太空刹车”,被月球捕获,进入了近月点约100km的环月轨道,如图所示,则下列说法中正确的是( )
A.“嫦娥四号”的发射速度大于第二宇宙速度
B.“嫦娥四号”在100km环月轨道运行通过P点时的加速度和在椭圆环月轨道运行通过P点时加速度相同
C.“嫦娥四号”在100km环月轨道运动的周期等于椭圆环月轨道运动的周期
D.“嫦娥四号”在地月转移轨道经过P点时和在100km环月轨道经过P点时速度相同
B
月球
P
100km环月轨道
椭圆环月轨道
地月转移轨道
C.100km环月轨道半径为r,椭圆轨道的半长轴为a,
根据开普勒第三定律得:
a
r
由于r > a
解:
A.“嫦娥四号”没有挣脱地球的引力,发射速度小于第一宇宙速度;A错
B.引力相同,a相同;B正确
所以 T1> T2
D.在地月转移轨道上的P点减速进入100km环月轨道,
所以两次经过P点时速度不同,
D不正确。
典例3
变式3:人造飞船首先进入的是距地面高度近地点为200km,远地点为340km的椭圆轨道,在飞行第5圈的时候,飞船从椭圆轨道运行到以远地点为半径的圆形轨道上,如图所示,试处理下面几个问题(地球的半径R等于6370千米,g=9.8m/s2):
(1)飞船在椭圆轨道1上运行,Q点为近地点,P为远地点,当飞船运动到P点时点火,使飞船沿圆轨道2运行,以下说法正确的是( )
A.飞船在Q点的万有引力大于该点所需的向心力
B.飞船在P点的万有引力大于该点所需的向心力
C.飞船在轨道1上P点的速度小于在轨道2上P点的速度
D.飞船在轨道1上P点的加速度大于在轨道2上P点的加速度
(2)假设由于飞船的特殊需要,一艘原来在轨道运行的飞船前往与之对接,则飞船一定是 ( )
A.从较低轨道上加速 B.从较高轨道上加速
C.从同一轨道上加速 D.从任意轨道上加速
月球
1
2
P
Q
BC
A
A.Q点速度大,所需向心力大于万有引力,做离心运动;
B.P点速度小,万有引力大于所需向心力,做近心运动。
解:
C.在P点点火加速,进入轨道2运行,所以轨道1上P点的速度小于轨道2上P点的速度,
D.飞船在两次在P点所受万有引力相同,所以加速度相同。
(1)
(2)
飞船对接可以从较低的轨道上加速,也可以从高轨道上减速。
变式3
四、双星与多星系统模型
模型一:双星模型
双星系统由两颗距离较近的星体组成,由于彼此的万有引力作用而绕连线上的某点做匀速圆周运动。
(1)周期T相同(角速度 相等);
(2)向心力大小相等(彼此间的万有引力提供所需向心力)。
O
A
B
规律总结
模型二:三星(共线)模型
三颗星体在一条直线上,两颗星体围绕中间的星体做圆周运动。
周期T相同(角速度 相等);
特点:
特点:
模型二:三星(正三角形)模型
(1)周期T相同(角速度 相等);
特点:
(2)向心力大小相等(两颗星对第三颗星的万有引力的合力提供所需向心力)。
典例4
典例4:如图为双星系统A、B绕其连线上的O点做匀速圆周运动的示意图,若A星的轨道半径大于B星的轨道半径,双星的总质量为M,双星间的距离为L,运动周期为T,则( )
A.A的质量一定大于B的质量
B.A的线速度一定大于B的线速度
C.L一定,M越大,T越大
D.M一定,L越大,T越大
O
A
B
解:
BD
总质量:
周期:
RA
RB
L
变式4:(2019河北石家庄质检)太空中存在一些离其他恒星很远的,由三颗星组成的三星系统,可忽略其他星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星始终在一条直线上;另一种是三角形三星系统——三颗星位于等边三角形的三个顶点上。已知某直线三星系统A每颗星体的质量均为m,相邻两颗星中心间的距离都为R,某三角形三星系统B的每颗星体的质量恰好也均为m,且三星系统A外侧的两颗星做匀速圆周运动的周期和三星系统B每颗星做匀速圆周运动的周期相等。引力常量为G,则( )
A.三星系统A外侧两颗星运动的线速度大小为
B.三星系统A外侧两颗星运动的角速度大小为
C.三星系统B的运动周期为
D.三星系统B任意两颗星体中心间的距离为
变式4
R
R
m
m
m
变式4
解:
L
L
L
R1
R1
R1
m
m
m
设三角形三星系统中两星之间的距离为L,三颗星体做匀速圆周运动的半径为R1
F合
F1
F1
在直线三星系统中,合力提供向心力
B、C正确
D正确
变式4:(2019河北石家庄质检)太空中存在一些离其他恒星很远的,由三颗星组成的三星系统,可忽略其他星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星始终在一条直线上;另一种是三角形三星系统——三颗星位于等边三角形的三个顶点上。已知某直线三星系统A每颗星体的质量均为m,相邻两颗星中心间的距离都为R,某三角形三星系统B的每颗星体的质量恰好也均为m,且三星系统A外侧的两颗星做匀速圆周运动的周期和三星系统B每颗星做匀速圆周运动的周期相等。引力常量为G,则( )
A.三星系统A外侧两颗星运动的线速度大小为
B.三星系统A外侧两颗星运动的角速度大小为
C.三星系统B的运动周期为
D.三星系统B任意两颗星体中心间的距离为
变式4
BCD
第六章 万有引力与航天
总结
万有引力与航天
1.开普勒三定律:
轨道定律
面积定律
周期定律
2.万有引力定律:
3.万有引力理论的成就:
测量地球质量
估算天体密度
“登高望远”
4.宇宙航行:
(1)宇宙速度
(2)人造卫星
5.经典力学的适用范围:
宏观、低速、弱引力
6.狭义相对论:
(1)地球表面:
(2)星体环绕:
发现未知天体
基本思路:万有引力提供向心力
“黄金代换”
“预测未来”
规律总结
一、天体质量和密度的求解方法:
(1)自立更生法:
利用天体表面的重力加速度g和天体的半径R:
利用卫星绕天体做匀速圆周运动的半径r和周期T.
①
③若卫星在天体表面附近运行时,可认为轨道半径r等于
天体半径R,则天体密度
②若已知天体的半径R,
只要测出卫星环绕天体表面运行的周期T,就可估算中心天体的密度。
(2)借助外援法:
典例1:(2019安徽合肥质检)已知地球和月球的半径之比为4:1,其表面重力加速度之比为6:1,则地球和月球的密度之比为( )
A.2:3, B.3:2, C.4:1, D.6:1
所以地球和月球的密度之比为:
B
解析:
在星球表面的物体,重力和万有引力相等,
解得质量为:
则密度为:
典例1
变式1(多选)(2019唐山模拟)人类将在未来登陆火星已知人造卫星A绕火星做匀速圆周运动所能达到的最大速度为v,最小周期为T,现有人造卫星B绕火星做匀速圆周运动,运行半径是火星半径的n倍,引力常量为G,则( )
B错
A对
解析:
AC
变式1
C对
D错
二、卫星运行问题的关键点:
(2)理解掌握第一宇宙速度的意义、推导过程及两个表达式
(3)灵活应用同步卫星的特点,注意同步卫星与地球赤道上物体的运动规律的区别和联系。
熟练记忆这几个关系式
R:地球半径,
g:地球表面重力加速度。
规律总结
特别提醒:赤道上物体转动所需的向心力不等于万有引力。
比较线速度大小:
比较向心加速度大小:
二者周期T相同
(角速度 相等)
典例2:2018年12月27日,“北斗三号”基本系统已完成建设,开始提供全球服务,其导航系统中部分卫星运行轨道如图所示,a为极地卫星,b为地球同步卫星,c为倾斜轨道卫星,其轨道平面与赤道平面有一定的夹角,周期与地球自转周期相同,下列说法正确的是( )
A.卫星a的线速度比卫星c的线速度小
B.卫星b的向心加速度比卫星c的向心加速度大
C.卫星b和卫星c的线速度大小相等
D.卫星a的机械能一定比卫星b的机械能大
a
c
b
解:
A不正确
B不正确
C.由A中的表达式可知:C正确
D.由于不知道卫星的质量关系,
D不正确
卫星a的机械能和卫星b的机械能的关系,
C
典例2
故无法判断
变式2.同步卫星与地心的距离为r,运行速率为v1向心加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则下列比值正确的是( )
a1
a2
a2
v2
v1
同步卫星
D
比较同步卫星、近地卫星和赤道上物体的线速度,角速度,周期和向心加速度的大小。
课后练习:
解析:
变式2
三、卫星变轨问题
1.发射(离心运动):卫星在轨道Ⅰ上的Q点加速进入Ⅱ轨道,在Ⅱ轨道上的P点加速进入Ⅲ轨道。
2.回收(近心运动):卫星在轨道Ⅲ上的P点减速进入Ⅱ轨道,在Ⅱ轨道上的Q点减速进入Ⅰ轨道。
vQ2 vQ1,
>
vP3 vP2
>
aQ2 = aQ1,
aP3 = aP2
月球
Ⅰ
Ⅱ
Ⅲ
P
Q
3.Ⅰ、Ⅱ轨道上Q点,Ⅱ、Ⅲ轨道上P点的速度和加速度的大小关系。
规律总结
典例3(2019河南郑州预测)“嫦娥四号”探测器成功发射,之后实施近月制动,顺利完成“太空刹车”,被月球捕获,进入了近月点约100km的环月轨道,如图所示,则下列说法中正确的是( )
A.“嫦娥四号”的发射速度大于第二宇宙速度
B.“嫦娥四号”在100km环月轨道运行通过P点时的加速度和在椭圆环月轨道运行通过P点时加速度相同
C.“嫦娥四号”在100km环月轨道运动的周期等于椭圆环月轨道运动的周期
D.“嫦娥四号”在地月转移轨道经过P点时和在100km环月轨道经过P点时速度相同
B
月球
P
100km环月轨道
椭圆环月轨道
地月转移轨道
C.100km环月轨道半径为r,椭圆轨道的半长轴为a,
根据开普勒第三定律得:
a
r
由于r > a
解:
A.“嫦娥四号”没有挣脱地球的引力,发射速度小于第一宇宙速度;A错
B.引力相同,a相同;B正确
所以 T1> T2
D.在地月转移轨道上的P点减速进入100km环月轨道,
所以两次经过P点时速度不同,
D不正确。
典例3
变式3:人造飞船首先进入的是距地面高度近地点为200km,远地点为340km的椭圆轨道,在飞行第5圈的时候,飞船从椭圆轨道运行到以远地点为半径的圆形轨道上,如图所示,试处理下面几个问题(地球的半径R等于6370千米,g=9.8m/s2):
(1)飞船在椭圆轨道1上运行,Q点为近地点,P为远地点,当飞船运动到P点时点火,使飞船沿圆轨道2运行,以下说法正确的是( )
A.飞船在Q点的万有引力大于该点所需的向心力
B.飞船在P点的万有引力大于该点所需的向心力
C.飞船在轨道1上P点的速度小于在轨道2上P点的速度
D.飞船在轨道1上P点的加速度大于在轨道2上P点的加速度
(2)假设由于飞船的特殊需要,一艘原来在轨道运行的飞船前往与之对接,则飞船一定是 ( )
A.从较低轨道上加速 B.从较高轨道上加速
C.从同一轨道上加速 D.从任意轨道上加速
月球
1
2
P
Q
BC
A
A.Q点速度大,所需向心力大于万有引力,做离心运动;
B.P点速度小,万有引力大于所需向心力,做近心运动。
解:
C.在P点点火加速,进入轨道2运行,所以轨道1上P点的速度小于轨道2上P点的速度,
D.飞船在两次在P点所受万有引力相同,所以加速度相同。
(1)
(2)
飞船对接可以从较低的轨道上加速,也可以从高轨道上减速。
变式3
四、双星与多星系统模型
模型一:双星模型
双星系统由两颗距离较近的星体组成,由于彼此的万有引力作用而绕连线上的某点做匀速圆周运动。
(1)周期T相同(角速度 相等);
(2)向心力大小相等(彼此间的万有引力提供所需向心力)。
O
A
B
规律总结
模型二:三星(共线)模型
三颗星体在一条直线上,两颗星体围绕中间的星体做圆周运动。
周期T相同(角速度 相等);
特点:
特点:
模型二:三星(正三角形)模型
(1)周期T相同(角速度 相等);
特点:
(2)向心力大小相等(两颗星对第三颗星的万有引力的合力提供所需向心力)。
典例4
典例4:如图为双星系统A、B绕其连线上的O点做匀速圆周运动的示意图,若A星的轨道半径大于B星的轨道半径,双星的总质量为M,双星间的距离为L,运动周期为T,则( )
A.A的质量一定大于B的质量
B.A的线速度一定大于B的线速度
C.L一定,M越大,T越大
D.M一定,L越大,T越大
O
A
B
解:
BD
总质量:
周期:
RA
RB
L
变式4:(2019河北石家庄质检)太空中存在一些离其他恒星很远的,由三颗星组成的三星系统,可忽略其他星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星始终在一条直线上;另一种是三角形三星系统——三颗星位于等边三角形的三个顶点上。已知某直线三星系统A每颗星体的质量均为m,相邻两颗星中心间的距离都为R,某三角形三星系统B的每颗星体的质量恰好也均为m,且三星系统A外侧的两颗星做匀速圆周运动的周期和三星系统B每颗星做匀速圆周运动的周期相等。引力常量为G,则( )
A.三星系统A外侧两颗星运动的线速度大小为
B.三星系统A外侧两颗星运动的角速度大小为
C.三星系统B的运动周期为
D.三星系统B任意两颗星体中心间的距离为
变式4
R
R
m
m
m
变式4
解:
L
L
L
R1
R1
R1
m
m
m
设三角形三星系统中两星之间的距离为L,三颗星体做匀速圆周运动的半径为R1
F合
F1
F1
在直线三星系统中,合力提供向心力
B、C正确
D正确
变式4:(2019河北石家庄质检)太空中存在一些离其他恒星很远的,由三颗星组成的三星系统,可忽略其他星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式:一种是直线三星系统——三颗星始终在一条直线上;另一种是三角形三星系统——三颗星位于等边三角形的三个顶点上。已知某直线三星系统A每颗星体的质量均为m,相邻两颗星中心间的距离都为R,某三角形三星系统B的每颗星体的质量恰好也均为m,且三星系统A外侧的两颗星做匀速圆周运动的周期和三星系统B每颗星做匀速圆周运动的周期相等。引力常量为G,则( )
A.三星系统A外侧两颗星运动的线速度大小为
B.三星系统A外侧两颗星运动的角速度大小为
C.三星系统B的运动周期为
D.三星系统B任意两颗星体中心间的距离为
变式4
BCD
