初中数学人教版八年级下册 第十七章 勾股定理 复习课件(34张PPT)
文档属性
| 名称 | 初中数学人教版八年级下册 第十七章 勾股定理 复习课件(34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 912.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 11:38:57 | ||
图片预览









文档简介
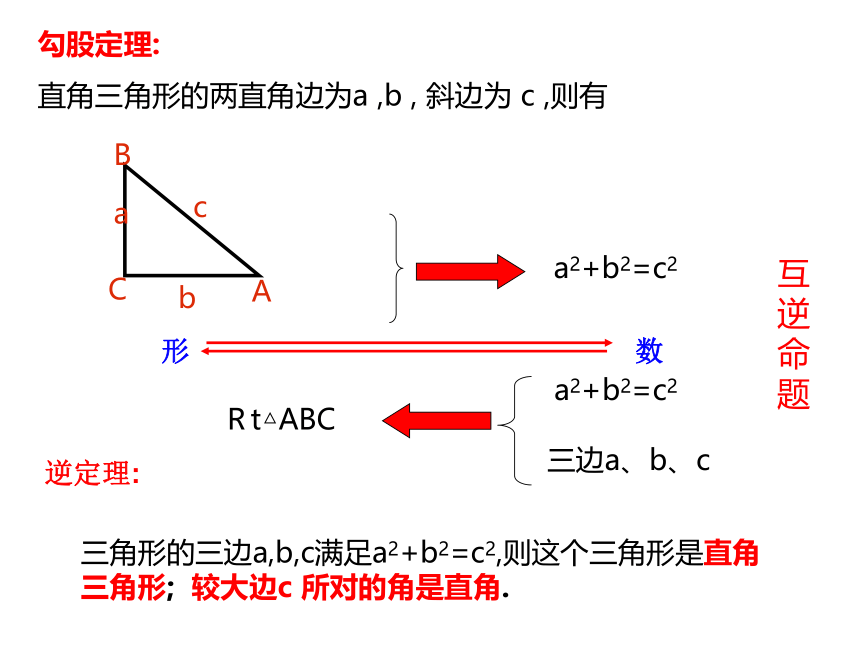
课件34张PPT。 勾股定理复习课 第一章:你还记得吗?a2+b2=c2形 数a2+b2=c2三边a、b、cRt△ABC互逆命题勾股定理:
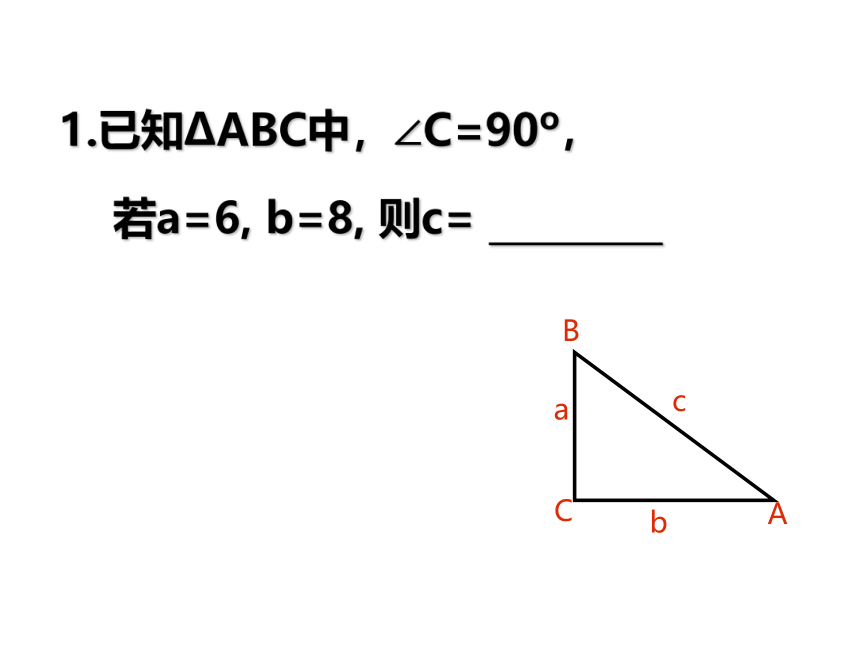
直角三角形的两直角边为a ,b , 斜边为 c ,则有三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.逆定理: 第二章:我们一起练习吧!若a=6, b=8, 则c= _________1.已知ΔABC中,∠C=90o,
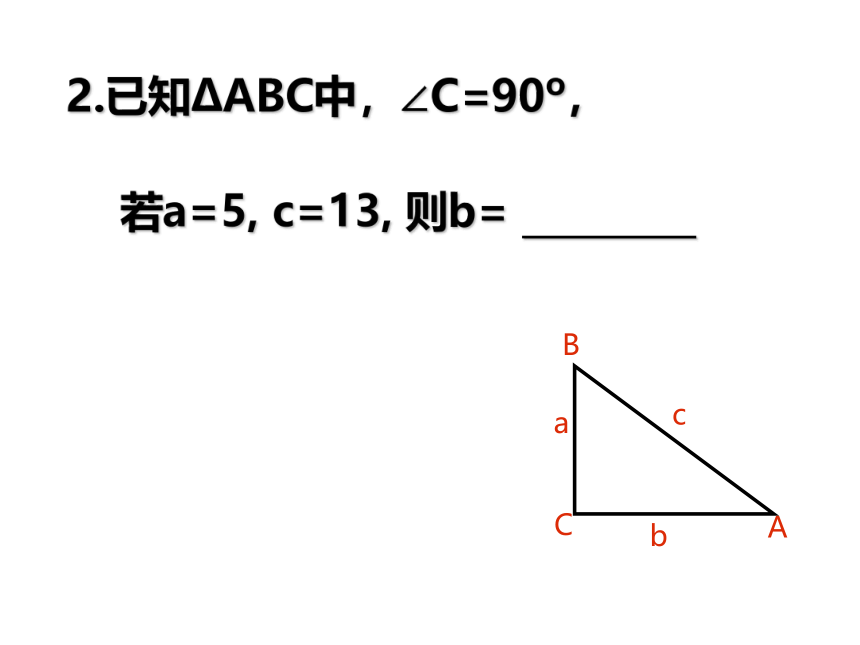
若a=5, c=13, 则b= _________2.已知ΔABC中,∠C=90o,
3.判断:下面以a、b、c 为边的三角形
是不是直角三角形? a=0.5,b=1.3,c=1.24.判断:下面以a、b、c 为边的三角形
是不是直角三角形? a=2,b=3,c=45.下列不是一组勾股数的是( )
A、5、12、13 B、
C、12、16、20 D、 7、24、25 B勾股数的妙用:你能速算吗?3.已知直角三角形中,∠c=90°,
(1)a=3,b=4,c=_____
(2)a=9,b=____c=15
(3)a=____,b=40,c=50
(4)a=24,b=32,c=________
(5)a=5,b=_______,c=13
(6)a=_____,b=36,c=39
(7)a=25,b=60,c=________
5123040121565你计算的很快呀,怎么做的?跟我们分享一下吧!6.已知数7和24,请你再写一个整数,使得这个数正好是一个直角三角形第三边的长,这个数可以是 ___________. 7.一个直角三角形的三边长是不大于10的三个连续的偶数,则它的周长是 __________. 第三章:我们一起闯关吧吧! 关卡1:分类讨论思想 2.三角形ABC中,AB=10,AC=17,BC边上的高线 AD=8,求BC的长。25或71017817108分类讨论思想: 1.直角三角形中,已知两边的长、另一边不知道时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。分类讨论思想,在直角三角形中的规律总结。 关卡2:方程思想1、小强想知道学校旗杆的高,他发现旗杆顶端的
绳子垂到地面还多1米,当他把绳子的下端拉开5米
后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(X+1)米x米2、折叠矩形ABCD的一边AD,点D落在BC边上的
点F处,已知AB=8CM,BC=10CM,求CF和EC的长.ABCDEF810106X8-X48-X方程思想: 关卡3:展开思想1.小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是3米、4米、12米,那么,能
放入电梯内的竹竿的最大长度是多少米?x如果电梯的长、宽、高分别是3米、4米、12米,那么,能
放入电梯内的竹竿的最大长度是多少米?2.如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20232323ABC
?
?
3.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定 BB8OA2蛋糕ACB8周长的一半
6 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。展开思想: 第四章:知识系统梳理 第五章:活学活用 1.小区里有一块四边形的绿化带,其中∠B=900,AB=3,BC=4,CD=12,AD=13,
你能求出绿化带的面积吗?
2.小区里有一块四边形的绿化带,∠B=900,
AB=3,BC=4,CD=12,AD=13,
你能求出绿化带的面积吗?
3.如图,在三角形ABC中,AB=AC,D在BC的延
长线上,求证:AD2-AB2=BD·CD
ABCD
直角三角形的两直角边为a ,b , 斜边为 c ,则有三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.逆定理: 第二章:我们一起练习吧!若a=6, b=8, 则c= _________1.已知ΔABC中,∠C=90o,
若a=5, c=13, 则b= _________2.已知ΔABC中,∠C=90o,
3.判断:下面以a、b、c 为边的三角形
是不是直角三角形? a=0.5,b=1.3,c=1.24.判断:下面以a、b、c 为边的三角形
是不是直角三角形? a=2,b=3,c=45.下列不是一组勾股数的是( )
A、5、12、13 B、
C、12、16、20 D、 7、24、25 B勾股数的妙用:你能速算吗?3.已知直角三角形中,∠c=90°,
(1)a=3,b=4,c=_____
(2)a=9,b=____c=15
(3)a=____,b=40,c=50
(4)a=24,b=32,c=________
(5)a=5,b=_______,c=13
(6)a=_____,b=36,c=39
(7)a=25,b=60,c=________
5123040121565你计算的很快呀,怎么做的?跟我们分享一下吧!6.已知数7和24,请你再写一个整数,使得这个数正好是一个直角三角形第三边的长,这个数可以是 ___________. 7.一个直角三角形的三边长是不大于10的三个连续的偶数,则它的周长是 __________. 第三章:我们一起闯关吧吧! 关卡1:分类讨论思想 2.三角形ABC中,AB=10,AC=17,BC边上的高线 AD=8,求BC的长。25或71017817108分类讨论思想: 1.直角三角形中,已知两边的长、另一边不知道时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。分类讨论思想,在直角三角形中的规律总结。 关卡2:方程思想1、小强想知道学校旗杆的高,他发现旗杆顶端的
绳子垂到地面还多1米,当他把绳子的下端拉开5米
后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(X+1)米x米2、折叠矩形ABCD的一边AD,点D落在BC边上的
点F处,已知AB=8CM,BC=10CM,求CF和EC的长.ABCDEF810106X8-X48-X方程思想: 关卡3:展开思想1.小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是3米、4米、12米,那么,能
放入电梯内的竹竿的最大长度是多少米?x如果电梯的长、宽、高分别是3米、4米、12米,那么,能
放入电梯内的竹竿的最大长度是多少米?2.如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20232323ABC
?
?
3.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定 BB8OA2蛋糕ACB8周长的一半
6 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。展开思想: 第四章:知识系统梳理 第五章:活学活用 1.小区里有一块四边形的绿化带,其中∠B=900,AB=3,BC=4,CD=12,AD=13,
你能求出绿化带的面积吗?
2.小区里有一块四边形的绿化带,∠B=900,
AB=3,BC=4,CD=12,AD=13,
你能求出绿化带的面积吗?
3.如图,在三角形ABC中,AB=AC,D在BC的延
长线上,求证:AD2-AB2=BD·CD
ABCD
