人教五四学制版 六年级数学下册8.2 整式的加减数学活动——探究月历中的数字规律 课件(共18张PPT)
文档属性
| 名称 | 人教五四学制版 六年级数学下册8.2 整式的加减数学活动——探究月历中的数字规律 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 07:26:34 | ||
图片预览






文档简介
课件18张PPT。第二章《整式的加减》数学活动课
——探究月历中的数字规律
一、情景引入万圣节迈入数学生命
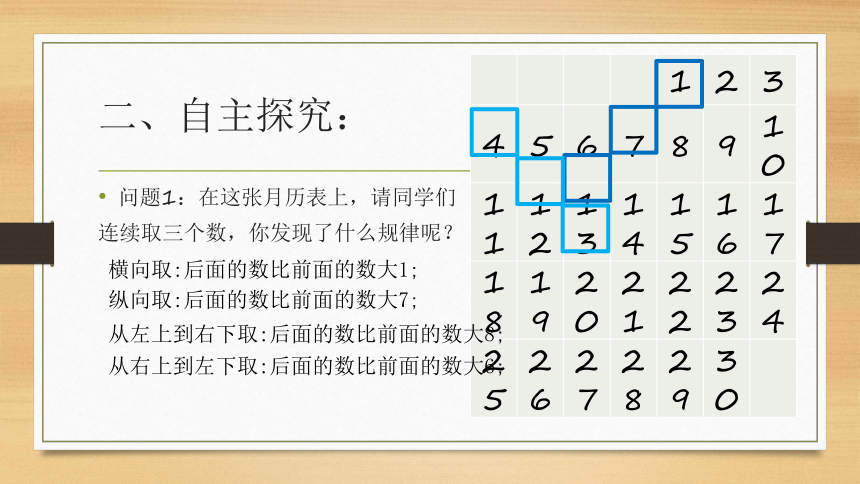
的新篇章!二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?横向取:后面的数比前面的数大1;纵向取:后面的数比前面的数大7;二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?横向取:后面的数比前面的数大1;纵向取:后面的数比前面的数大7;从左上到右下取:后面的数比前面的数大8;从右上到左下取:后面的数比前面的数大6;二、自主探究:问题2:如何表示上述的规律呢?a横向连续取:a,a+1,a+2纵向连续取:a,a+7,a+14从左上到右下连续取: a,a+8,a+16
从右上到左下连续取: a,a+6,a+12
用字母表示数,进入代数学的标志.用字母表示数的创新意识!设取的第一个数是a话说代数公元250年前后,古希腊数学家丢番图写了一本书《算术》,首次用字母表示未知数,建立了方程,被西方人尊称为代数学的鼻祖;
十六世纪中旬,法国数学家维耶特第一次应用字母来表示已知数(在他之前字母仅是用以表示未知数),它使得很复杂的数学想法变得易于表述和了解,更容易看出问题的结构和规律,并能够变换为更简明的形式,是数学上一项重大的变革。同期的法国数学家韦达在系统地使用字母表示数后,引出了大量的数学发现,解决很多古代的复杂问题,故被尊称为代数学之父;
二十世纪三十年代,荷兰数学家范·德·瓦尔登写了《代数学》,详细阐述了什么是代数学。
代数学是研究数、数量、关系与结构的数学分支。代数学可分为初等代数学和抽象代数学两部分。练习1.如图是2018年10月份的日历表,用一个
圈横着圈住3个数,这三个数的和可能是( )
(A)71 (B)59 (C) 40 (D) 27 D不同策略的比较选择! a –1 +a+a+1=3a a –7 +a+a+7=3a a –8 +a+a+8=3a a –6 +a+a+6=3a连续三个数之和=3 *中间的数三、归纳提升:问题3:连续取的三个数的和有什么规律吗?你能证明吗? 方法:用字母表示数进行运算推理证明四、引领发展:问题4:按如图所示的方式连续取3*3方格的九个数,请同学们以小组为单位进行研究:这些数之问有什么规律吗?如何证明这个规律呢?
四、引领发展:发现:
9个数的和=中心数的9倍问题5:以上结论,对任何一个
月的月历都成立吗?观察特例证明规律探索规律的一般思路:用符号(或字母)表示实际问题的一般规律,并用运算来推理论证一般规律。猜想规律特殊与一般的数学思想1、如图,在排成每行七天的月历表中取下一个3×3的方块(包含9个数字)。若所有日期之和为 189 ,则n的值为( )
A. 15 B.11 C. 21 D.24C五、成效评价2.如图,用一个正方形框出9个数,要使这个正方形框出的9个数之和等于450,这是否可能?若可能,求出框中最大数和最小数。若不可能,说明理由.3. 如图所示,两个不同图形选中的4个数,对角线上的两个数之和是否存在规律呢?六、能力提升:“我是小小设计师”你能设计一个其他形状的数框,使其选中的数字存在一定的规律吗?
用字母表示你发现的规律,并给出证明.六、课堂小结1.本节课学到了哪些数学方法?
2.本节课体验到了哪些数学思想?七、课后作业校本作业
的新篇章!二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?横向取:后面的数比前面的数大1;纵向取:后面的数比前面的数大7;二、自主探究:问题1:在这张月历表上,请同学们
连续取三个数,你发现了什么规律呢?横向取:后面的数比前面的数大1;纵向取:后面的数比前面的数大7;从左上到右下取:后面的数比前面的数大8;从右上到左下取:后面的数比前面的数大6;二、自主探究:问题2:如何表示上述的规律呢?a横向连续取:a,a+1,a+2纵向连续取:a,a+7,a+14从左上到右下连续取: a,a+8,a+16
从右上到左下连续取: a,a+6,a+12
用字母表示数,进入代数学的标志.用字母表示数的创新意识!设取的第一个数是a话说代数公元250年前后,古希腊数学家丢番图写了一本书《算术》,首次用字母表示未知数,建立了方程,被西方人尊称为代数学的鼻祖;
十六世纪中旬,法国数学家维耶特第一次应用字母来表示已知数(在他之前字母仅是用以表示未知数),它使得很复杂的数学想法变得易于表述和了解,更容易看出问题的结构和规律,并能够变换为更简明的形式,是数学上一项重大的变革。同期的法国数学家韦达在系统地使用字母表示数后,引出了大量的数学发现,解决很多古代的复杂问题,故被尊称为代数学之父;
二十世纪三十年代,荷兰数学家范·德·瓦尔登写了《代数学》,详细阐述了什么是代数学。
代数学是研究数、数量、关系与结构的数学分支。代数学可分为初等代数学和抽象代数学两部分。练习1.如图是2018年10月份的日历表,用一个
圈横着圈住3个数,这三个数的和可能是( )
(A)71 (B)59 (C) 40 (D) 27 D不同策略的比较选择! a –1 +a+a+1=3a a –7 +a+a+7=3a a –8 +a+a+8=3a a –6 +a+a+6=3a连续三个数之和=3 *中间的数三、归纳提升:问题3:连续取的三个数的和有什么规律吗?你能证明吗? 方法:用字母表示数进行运算推理证明四、引领发展:问题4:按如图所示的方式连续取3*3方格的九个数,请同学们以小组为单位进行研究:这些数之问有什么规律吗?如何证明这个规律呢?
四、引领发展:发现:
9个数的和=中心数的9倍问题5:以上结论,对任何一个
月的月历都成立吗?观察特例证明规律探索规律的一般思路:用符号(或字母)表示实际问题的一般规律,并用运算来推理论证一般规律。猜想规律特殊与一般的数学思想1、如图,在排成每行七天的月历表中取下一个3×3的方块(包含9个数字)。若所有日期之和为 189 ,则n的值为( )
A. 15 B.11 C. 21 D.24C五、成效评价2.如图,用一个正方形框出9个数,要使这个正方形框出的9个数之和等于450,这是否可能?若可能,求出框中最大数和最小数。若不可能,说明理由.3. 如图所示,两个不同图形选中的4个数,对角线上的两个数之和是否存在规律呢?六、能力提升:“我是小小设计师”你能设计一个其他形状的数框,使其选中的数字存在一定的规律吗?
用字母表示你发现的规律,并给出证明.六、课堂小结1.本节课学到了哪些数学方法?
2.本节课体验到了哪些数学思想?七、课后作业校本作业
