北师大版八年级下册数学 5.4分式方程 课件(第2课时 共15张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 5.4分式方程 课件(第2课时 共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第五章 分 式与分式方程
5.4 分式方程(二)
知识回顾
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款,已知第一次捐款总额为4800元,第二次捐款总额5000元,第二次捐款人比第一次多20人,而且两次人均捐款额正好相等,如果设第一次捐款的人数为x人,那么你能列出分式方程吗?
捐款总额 捐款人 数 人均捐款额
第一次 4800元 x
第二次 5000元
X+20
〓
怎样解这个方程呢?
你能否从中总结出分式方程 的解法
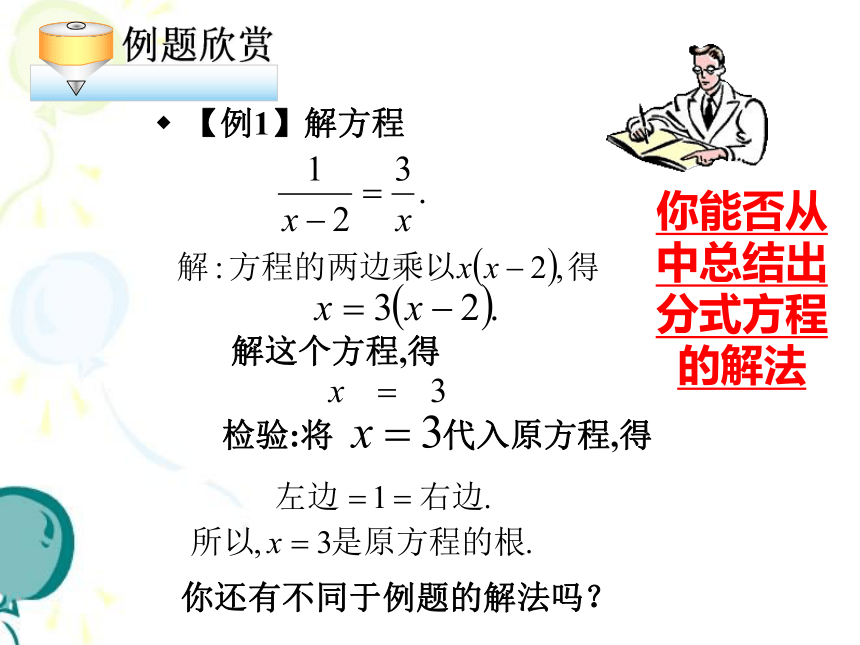
【例1】解方程
例题欣赏
你还有不同于例题的解法吗?
解这个方程,得
检验:将 代入原方程,得
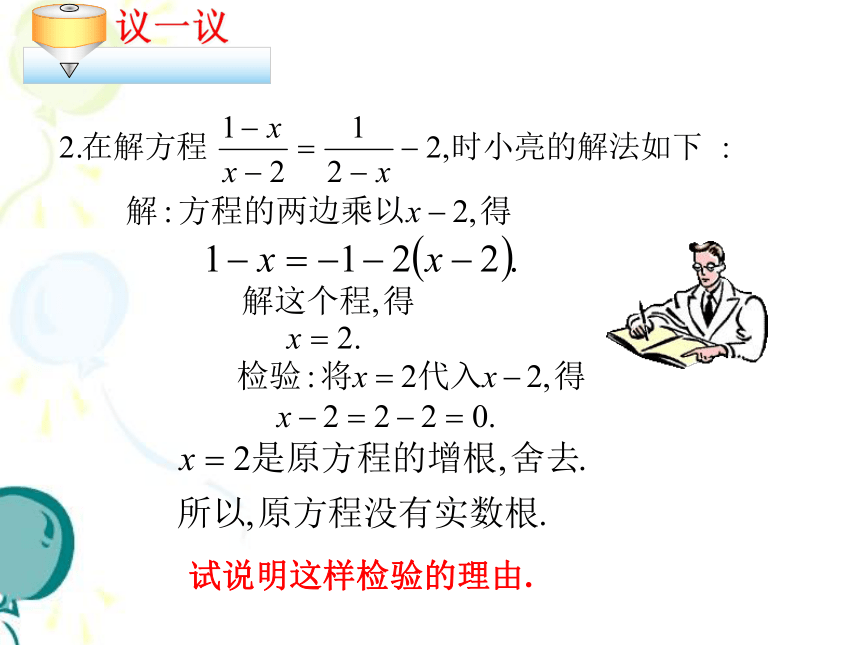
议一议
你认为x=2是原方程的根吗?为什么?与同伴交流你的看法或做法.?
发现新大陆
在上面的方程中,x=2不是原方程的根,因为它使得原分式方程的分母为零,我们你它为原方程的增根.
产生增根的原因,是我们在方程的两边同乘了一个可能使分母为零的整式.
因此解分式方程可能产生增根,所以解分式方程 必须检验.
增根与验根
议一议
试说明这样检验的理由.
【例2】解方程
例题欣赏
说一说分式方程 的解法步骤有哪几步
你还有不同于例题的解法吗?
解分式方程一般需要哪几个步骤?
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
结论 :确定分式方程的解.
想一想,启迪思维
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
这里的检验要以计算正确为前提
切记:解分式方程一定要验根噢!
检验的方法:
用实战来证明自己
练一练
解下列分式方程
解分式方程容易犯的错误主要有:
去分母时,原方程的整式部分漏乘.
约去分母后,分子是多项式时, 要注意添括号.
增根不舍掉.
符号问题.
……
想一想
例3.当m的值为何值时分式方程
会产生增根?
解:方程两边都乘以 ,得
解这个方程,得
∵ 是原方程的增根
而原方程的曾根是
∴
解得
再来一例
①去分母
个整式方程
③检验
④得出结论,写答句。
②解这
小 结
一化二解三检验四结论
2 解分式方程的一般步骤是
1
去分母
分式方程
整式方程
求出根
两边乘以
最简公分母
值为零
检验
增根
(1).关于m的分式方程
有增根,则m=?
(2)解分式方程
大显身手
第五章 分 式与分式方程
5.4 分式方程(二)
知识回顾
为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款,已知第一次捐款总额为4800元,第二次捐款总额5000元,第二次捐款人比第一次多20人,而且两次人均捐款额正好相等,如果设第一次捐款的人数为x人,那么你能列出分式方程吗?
捐款总额 捐款人 数 人均捐款额
第一次 4800元 x
第二次 5000元
X+20
〓
怎样解这个方程呢?
你能否从中总结出分式方程 的解法
【例1】解方程
例题欣赏
你还有不同于例题的解法吗?
解这个方程,得
检验:将 代入原方程,得
议一议
你认为x=2是原方程的根吗?为什么?与同伴交流你的看法或做法.?
发现新大陆
在上面的方程中,x=2不是原方程的根,因为它使得原分式方程的分母为零,我们你它为原方程的增根.
产生增根的原因,是我们在方程的两边同乘了一个可能使分母为零的整式.
因此解分式方程可能产生增根,所以解分式方程 必须检验.
增根与验根
议一议
试说明这样检验的理由.
【例2】解方程
例题欣赏
说一说分式方程 的解法步骤有哪几步
你还有不同于例题的解法吗?
解分式方程一般需要哪几个步骤?
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
结论 :确定分式方程的解.
想一想,启迪思维
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
这里的检验要以计算正确为前提
切记:解分式方程一定要验根噢!
检验的方法:
用实战来证明自己
练一练
解下列分式方程
解分式方程容易犯的错误主要有:
去分母时,原方程的整式部分漏乘.
约去分母后,分子是多项式时, 要注意添括号.
增根不舍掉.
符号问题.
……
想一想
例3.当m的值为何值时分式方程
会产生增根?
解:方程两边都乘以 ,得
解这个方程,得
∵ 是原方程的增根
而原方程的曾根是
∴
解得
再来一例
①去分母
个整式方程
③检验
④得出结论,写答句。
②解这
小 结
一化二解三检验四结论
2 解分式方程的一般步骤是
1
去分母
分式方程
整式方程
求出根
两边乘以
最简公分母
值为零
检验
增根
(1).关于m的分式方程
有增根,则m=?
(2)解分式方程
大显身手
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
