人教版七年级下册数学 17.2 勾股定理的逆定理 测试题(解析版)
文档属性
| 名称 | 人教版七年级下册数学 17.2 勾股定理的逆定理 测试题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 00:00:00 | ||
图片预览

文档简介
17.2 勾股定理的逆定理 测试题
一.选择题
1. 下列几组数中不能作为直角三角形三边长度的是( )
A.a=7,b=24,c=25 B.a=1.5,b=2,c=2.5
C. D.a=15,b=8,c=17
2. 下列三角形中,不是直角三角形的是( )
A.三个内角之比为5∶6∶1 B. 一边上的中线等于这一边的一半
C.三边之长为20、21、29 D. 三边之比为1.5 : 2 : 3
3. 下列命题中,不正确的是( )
A. 三个角的度数之比为1:3:4的三角形是直角三角形;
B. 三边之比为1: :2的三角形是直角三角形;
C. 三个角的度数之比为1:2:2的三角形是直角三角形;
D. 三边之比为::2的三角形是直角三角形.
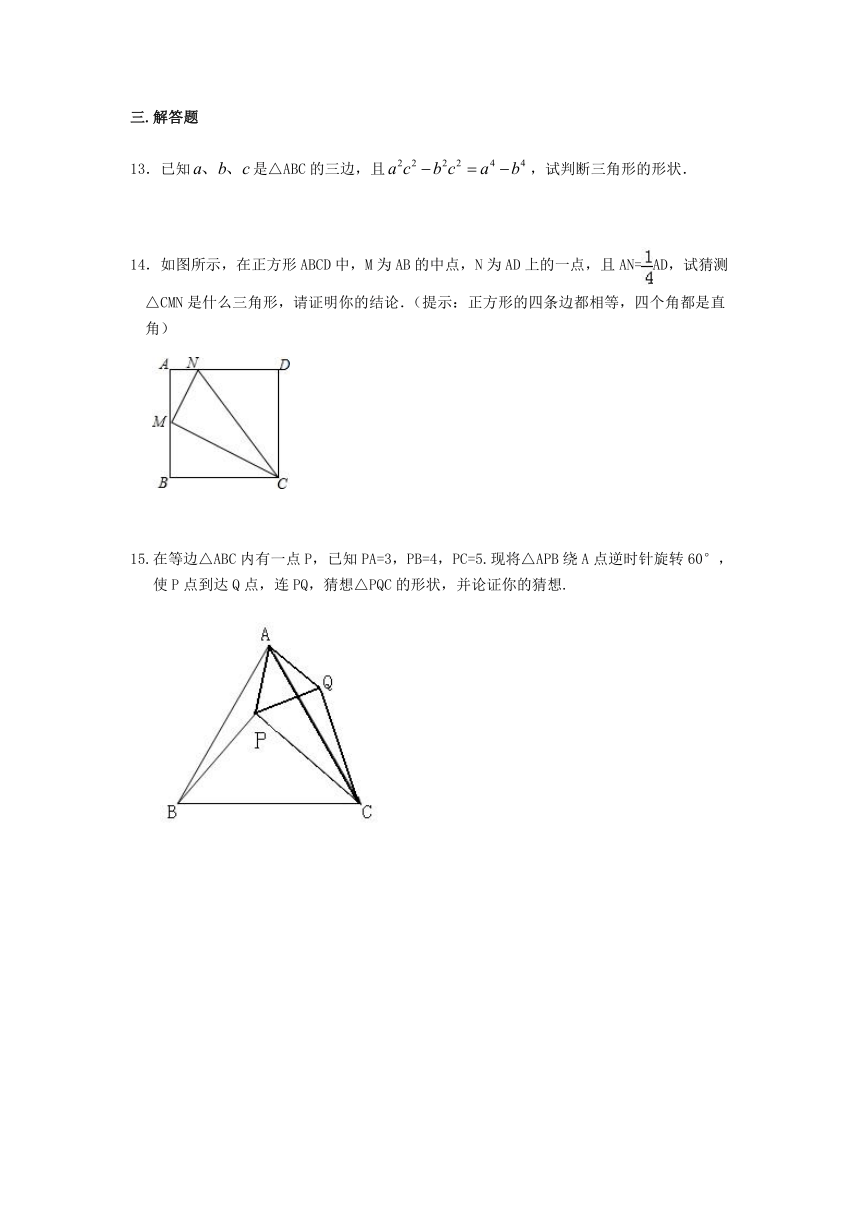
4. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH C.AB、CF、EF D.GH、AB、CD
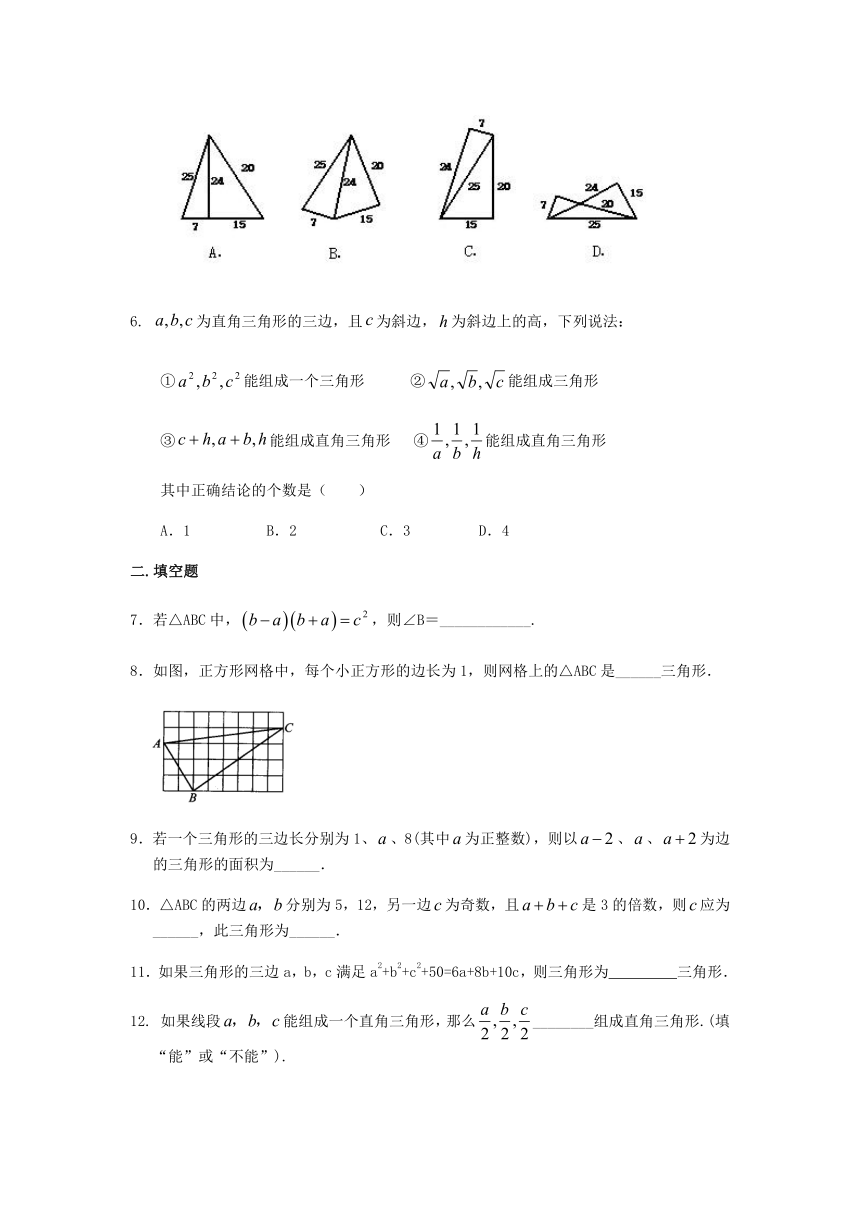
5.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
6. 为直角三角形的三边,且为斜边,为斜边上的高,下列说法:
①能组成一个三角形 ②能组成三角形
③能组成直角三角形 ④能组成直角三角形
其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二.填空题
7.若△ABC中,,则∠B=____________.
8.如图,正方形网格中,每个小正方形的边长为1,则网格上的△ABC是______三角形.
9.若一个三角形的三边长分别为1、、8(其中为正整数),则以、、为边的三角形的面积为______.
10.△ABC的两边分别为5,12,另一边为奇数,且是3的倍数,则应为______,此三角形为______.
11.如果三角形的三边a,b,c满足a2+b2+c2+50=6a+8b+10c,则三角形为 三角形.
12. 如果线段能组成一个直角三角形,那么________组成直角三角形.(填“能”或“不能”).
三.解答题
13.已知是△ABC的三边,且,试判断三角形的形状.
14.如图所示,在正方形ABCD中,M为AB的中点,N为AD上的一点,且AN=AD,试猜测△CMN是什么三角形,请证明你的结论.(提示:正方形的四条边都相等,四个角都是直角)
15.在等边△ABC内有一点P,已知PA=3,PB=4,PC=5.现将△APB绕A点逆时针旋转60°,使P点到达Q点,连PQ,猜想△PQC的形状,并论证你的猜想.
【答案与解析】
一.选择题
1.【答案】C;
【解析】解:A、满足勾股定理:72+242=252,故A选项不符合题意;
B、满足勾股定理:1.52+22=2.52,故B选项不符合题意;
C、不满足勾股定理,不是勾股数,故C选项符合题意;
D、满足勾股定理:152+82=172,故D选项不符合题意.
故选:C.
2.【答案】D;
【解析】D选项不满足勾股定理的逆定理.
3.【答案】C;
【解析】度数之比为1:2:2,则三角形内角分别为36°:72°:72°.
4.【答案】B;
【解析】,所以这三条线段能构成直角三角形.
5.【答案】C;
【解析】.
6.【答案】C;
【解析】因为,两边之和等于第三边,故不能组成一个三角形,①错误;因为,所以能组成三角形,②正确;因为,所以,即,③正确;因为,所以④正确.
二.填空题
7.【答案】90°;
【解析】由题意,所以∠B=90°.
8.【答案】直角;
【解析】=13,=52,=65,所以.
9.【答案】24;
【解析】∵7<<9,∴=8.
10.【答案】13;直角三角形;
【解析】7<<17.
11.【答案】直角;
【解析】解:∵a2+b2+c2+50=6a+8b+10c
∴a2+b2+c2﹣6a﹣8b﹣10c+50=0
即a2﹣6a+9+b2﹣8b+16+c2﹣10c+25=0
∴(a﹣3)2+(b﹣4)2+(c﹣5)2=0
∴a=3,b=4,c=5
∵a2+b2=c2
∴三角形为直角三角形.
12.【答案】能;
【解析】设为斜边,则,两边同乘以,得,即 .
三.解答题
13.【解析】
解:因为,
所以
所以或,
此三角形为等腰三角形或直角三角形.
14.【解析】
解:△CMN是直角三角形.理由如下:
设正方形ABCD的边长为4a,则AB=BC=CD=AD=4a.
∵M是AB的中点,
∴AM=BM=2a.
∵AN=AD,AD=4a,
∴AN=a,DN=3a.
∵在Rt△AMN中,满足AM2+AN2=MN2,且AM=2a,AN=a,
∴MN=a.
同理可得:MC=a,NC=5a.
∵MN2+MC2=(a)2+(a)2=25a2,NC2=(5a)2=25a2,
∴MN2+MC2=NC2,
∴△CMN是直角三角形.
15.【解析】
解:因为△APB绕A点逆时针旋转60°得到△AQC,
所以△APB≌△AQC,∠PAQ=60°,
所以AP=AQ=PQ=3,BP=CQ=4,
又因为PC=5,
所以△PQC是直角三角形.
