人教版七年级下册数学 8.2 消元-解二元一次方程组(加减消元)课件(共32张PPT)
文档属性
| 名称 | 人教版七年级下册数学 8.2 消元-解二元一次方程组(加减消元)课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 505.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-10 20:46:22 | ||
图片预览










文档简介
(共32张PPT)
8.2消元-解二元一次方程组
(加减消元)
人教版数学七年级下册
主要步骤:
基本思想:
写解
求解
代入
消去一个未知数
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思想是什么?
2、用代入法解方程组的主要步骤是什么?
一元
例1 解二元一次方程组
①
②
把 ①变形得
代入② ,不就消去 了!
①
②
把①变形得
可以直接代入②呀!
①
②
和
相同
(2x - 3y)–(2x + 5y)= 1 – 9
2x – 3y – 2x – 5y= – 8
①左边–②左边=①右边–②右边
– 8y = – 8
①
②
y=1
把y=1代入①,得x=2
所以原方程组的解是
所以原方程组的解是
解:由②-①, 得 8y=8
把y=1代入①,得
y=1
x=2
①
②
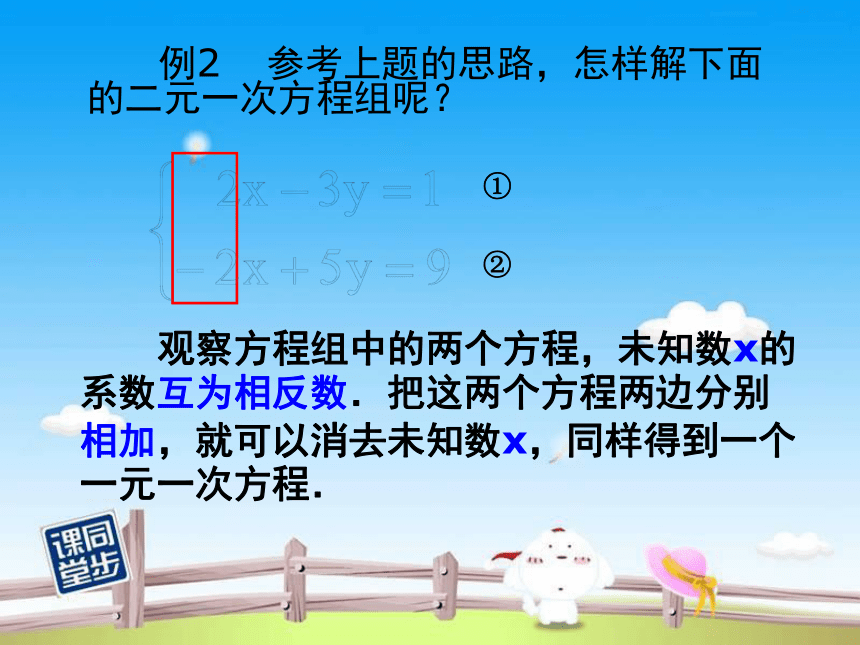
例2 参考上题的思路,怎样解下面的二元一次方程组呢?
①
②
观察方程组中的两个方程,未知数x的系数互为相反数.把这两个方程两边分别相加,就可以消去未知数x,同样得到一个一元一次方程.
①
②
解:由②+①,得 2y=10
y=5
把y=5代入①,得 x=8
所以原方程组的解是
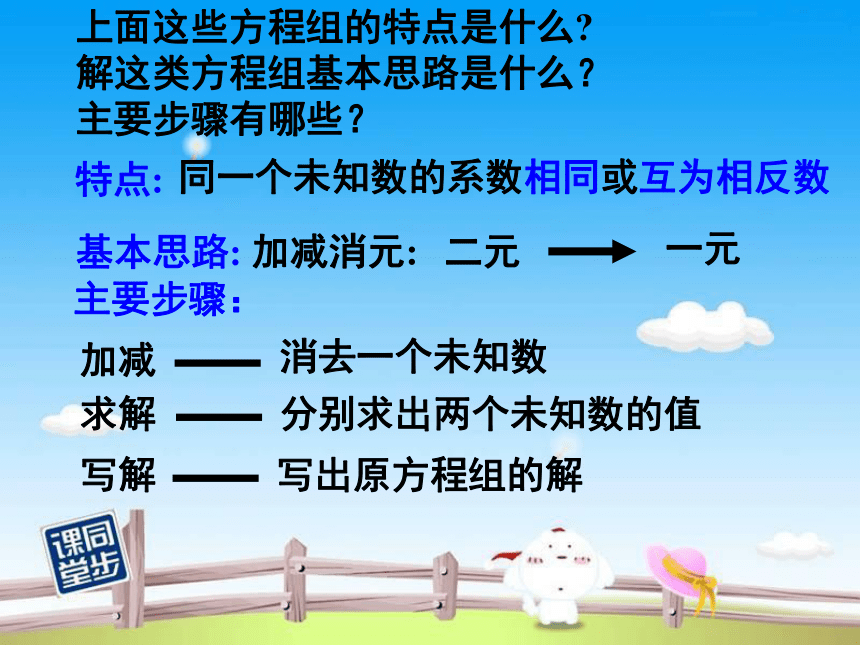
上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个未知数
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
问题.这两个方程直接相加减能消去未知
数吗?为什么?
①
②
当方程组中两方程不具备上述特点时,必须用等式性质来变形,即得到某未知数系数的绝对值相等的新方程组,从而为加减消元法解方程组创造条件.
例3 解二元一次方程组
解:由①×2,得 4x–6y=–2 ③
由②- ③,得 11y=11
y=1
把y=1代入①,得 x=1
所以原方程组的解是
①
②
解法2:通过由①×5,②×3,使关于y的系数互为相反数,从而可用加法解得.
①
②
解法1:通过由①×3,②×2,使关于x的系数相等,从而可用减法解得.
例4 解二元一次方程组
解:由①×3,得 6x–9y=–3 ③
由②×2,得 6x+10y=16 ④
由④ - ③,得 19y=19
y=1
把y=1 代入①,得 x=1
所以原方程组的解是
①
②
解:由①×5,得 10x – 15y= – 5 ③
由②×3,得 9x+15y=24 ④
由④ + ③, 得 19x=19
x=1
把x=1代入①,得 y=1
所以原方程组的解是
①
②
例5 解二元一次方程组
①
②
解:由① - ②,得 7x-35y=0
得 X=5y ③
把③2代入① ,得5×5y-3y=110
得 y=5
把y=5 代入③,得 x=25
所以原方程组的解是
②
①
例6. 用加减消元法解方程组
解:由①×6,得
2x+3y=4 ③
由②×4,得
2x - y=8 ④
由③-④,得 y= -1
所以原方程组的解是
把y= -1代入② ,
得
2(x+1)+3y=6
①
例7 解方程组
②
解: ① + ②,得 10000(x+y)=50000
X+y=5 ③
① - ②,得 6718(x-y)=6718
X-y=1 ④
③ +④,得 2x=6 ∴X=3
③ -④ ,得 2y=4 ∴y=2
所以原方程组的解是
ax+by=m ①
bx+ay=n ②
解: ① + ②,得 (a+b)(x+y)=m+n
X+y=c ③
① - ②,得 (a-b)(x-y)=m-n
X-y=d ④
③+④,得 2x=c+d ∴X=k1
③- ④,得 2y=c-d ∴y=k2
所以原方程组的解是
解: ① + ②,整理得 X+y=6 ③
① - ②,整理得 X-y=20 ④
所以原方程组的解是
例8. 解方程组
②
①
③+④,得 2x=26 ∴X=13
③- ④,得 2y=-14 ∴y=-7
得 a+b=3 ③
得 a-b=-1 ④
所以原方程组的解是
解:设
③+④,得 2a=2 ∴a=1
③- ④,得 2b=4 ∴b=2
∴x=13,y=-7
换元法
∴
例9 已知方程组 的解
是 则方程组
的解是 .
a+2=x
b-1=y
a+2=8.3
b-1=1.2
例10 关于x、y的方程组
的解满足3x+y=5,则k= .
3× + = 5
k=10
10
例10 关于x、y的方程组
的解满足3x+y=5,则k= .
解:①+②,得 3x+y=15-k
∵3x+y=5
∴15-k=5
∴K=10
10
①
②
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数 .
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数 .
x
一.填空题:
只要两边
只要两边
练习
二.选择题
1. 用加减法解方程组
6x+7y=-19 ①
6x-5y=17 ②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
三.指出下列方程组求解过程中有错误的步骤,并给予订正:
7x-4y=4
5x-4y=-4
解: ①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解: ①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
四.已知a、b满足方程组
则a+b=
5
分析:由②+①,得 3a+3b=15
①
②
∴ a+b=5
五.在解方程组
时,小张正
中的C得到方程组的解为 ,
程组中的a、b、c的值.
,小李由于看错了方程组
确的解是
试求方
解:∵c×1-3×2=5
∴c=11
?
í
ì
-
=
+
-
-
=
+
7
b
3
7
b
2
a
a
∴a=1,b=-4,c=11.
∵
∴
主要步骤:
基本思想:
写解
求解
加减
二元
一元
加减消元:
消去一个未知数
求出两个未知数的值
写出方程组的解
1.加减消元法解方程组的基本思想是什么?主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
2. 二元一次方程组解法有 .
代入法、加减法
作业
1、课本习题8.2 ,第 3 题.
2、思考题:
(1) 在解二元一次方程组中, 代入法
和加减法有什么异同点?
(2)解方程组
8.2消元-解二元一次方程组
(加减消元)
人教版数学七年级下册
主要步骤:
基本思想:
写解
求解
代入
消去一个未知数
分别求出两个未知数的值
写出方程组的解
变形
用一个未知数的代数式
表示另一个未知数
消元: 二元
1、解二元一次方程组的基本思想是什么?
2、用代入法解方程组的主要步骤是什么?
一元
例1 解二元一次方程组
①
②
把 ①变形得
代入② ,不就消去 了!
①
②
把①变形得
可以直接代入②呀!
①
②
和
相同
(2x - 3y)–(2x + 5y)= 1 – 9
2x – 3y – 2x – 5y= – 8
①左边–②左边=①右边–②右边
– 8y = – 8
①
②
y=1
把y=1代入①,得x=2
所以原方程组的解是
所以原方程组的解是
解:由②-①, 得 8y=8
把y=1代入①,得
y=1
x=2
①
②
例2 参考上题的思路,怎样解下面的二元一次方程组呢?
①
②
观察方程组中的两个方程,未知数x的系数互为相反数.把这两个方程两边分别相加,就可以消去未知数x,同样得到一个一元一次方程.
①
②
解:由②+①,得 2y=10
y=5
把y=5代入①,得 x=8
所以原方程组的解是
上面这些方程组的特点是什么?
解这类方程组基本思路是什么?
主要步骤有哪些?
主要步骤:
特点:
基本思路:
写解
求解
加减
二元
一元
加减消元:
消去一个未知数
分别求出两个未知数的值
写出原方程组的解
同一个未知数的系数相同或互为相反数
问题.这两个方程直接相加减能消去未知
数吗?为什么?
①
②
当方程组中两方程不具备上述特点时,必须用等式性质来变形,即得到某未知数系数的绝对值相等的新方程组,从而为加减消元法解方程组创造条件.
例3 解二元一次方程组
解:由①×2,得 4x–6y=–2 ③
由②- ③,得 11y=11
y=1
把y=1代入①,得 x=1
所以原方程组的解是
①
②
解法2:通过由①×5,②×3,使关于y的系数互为相反数,从而可用加法解得.
①
②
解法1:通过由①×3,②×2,使关于x的系数相等,从而可用减法解得.
例4 解二元一次方程组
解:由①×3,得 6x–9y=–3 ③
由②×2,得 6x+10y=16 ④
由④ - ③,得 19y=19
y=1
把y=1 代入①,得 x=1
所以原方程组的解是
①
②
解:由①×5,得 10x – 15y= – 5 ③
由②×3,得 9x+15y=24 ④
由④ + ③, 得 19x=19
x=1
把x=1代入①,得 y=1
所以原方程组的解是
①
②
例5 解二元一次方程组
①
②
解:由① - ②,得 7x-35y=0
得 X=5y ③
把③2代入① ,得5×5y-3y=110
得 y=5
把y=5 代入③,得 x=25
所以原方程组的解是
②
①
例6. 用加减消元法解方程组
解:由①×6,得
2x+3y=4 ③
由②×4,得
2x - y=8 ④
由③-④,得 y= -1
所以原方程组的解是
把y= -1代入② ,
得
2(x+1)+3y=6
①
例7 解方程组
②
解: ① + ②,得 10000(x+y)=50000
X+y=5 ③
① - ②,得 6718(x-y)=6718
X-y=1 ④
③ +④,得 2x=6 ∴X=3
③ -④ ,得 2y=4 ∴y=2
所以原方程组的解是
ax+by=m ①
bx+ay=n ②
解: ① + ②,得 (a+b)(x+y)=m+n
X+y=c ③
① - ②,得 (a-b)(x-y)=m-n
X-y=d ④
③+④,得 2x=c+d ∴X=k1
③- ④,得 2y=c-d ∴y=k2
所以原方程组的解是
解: ① + ②,整理得 X+y=6 ③
① - ②,整理得 X-y=20 ④
所以原方程组的解是
例8. 解方程组
②
①
③+④,得 2x=26 ∴X=13
③- ④,得 2y=-14 ∴y=-7
得 a+b=3 ③
得 a-b=-1 ④
所以原方程组的解是
解:设
③+④,得 2a=2 ∴a=1
③- ④,得 2b=4 ∴b=2
∴x=13,y=-7
换元法
∴
例9 已知方程组 的解
是 则方程组
的解是 .
a+2=x
b-1=y
a+2=8.3
b-1=1.2
例10 关于x、y的方程组
的解满足3x+y=5,则k= .
3× + = 5
k=10
10
例10 关于x、y的方程组
的解满足3x+y=5,则k= .
解:①+②,得 3x+y=15-k
∵3x+y=5
∴15-k=5
∴K=10
10
①
②
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数 .
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数 .
x
一.填空题:
只要两边
只要两边
练习
二.选择题
1. 用加减法解方程组
6x+7y=-19 ①
6x-5y=17 ②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是( )
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
三.指出下列方程组求解过程中有错误的步骤,并给予订正:
7x-4y=4
5x-4y=-4
解: ①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解: ①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
四.已知a、b满足方程组
则a+b=
5
分析:由②+①,得 3a+3b=15
①
②
∴ a+b=5
五.在解方程组
时,小张正
中的C得到方程组的解为 ,
程组中的a、b、c的值.
,小李由于看错了方程组
确的解是
试求方
解:∵c×1-3×2=5
∴c=11
?
í
ì
-
=
+
-
-
=
+
7
b
3
7
b
2
a
a
∴a=1,b=-4,c=11.
∵
∴
主要步骤:
基本思想:
写解
求解
加减
二元
一元
加减消元:
消去一个未知数
求出两个未知数的值
写出方程组的解
1.加减消元法解方程组的基本思想是什么?主要步骤有哪些?
变形
同一个未知数的系
数相同或互为相反数
2. 二元一次方程组解法有 .
代入法、加减法
作业
1、课本习题8.2 ,第 3 题.
2、思考题:
(1) 在解二元一次方程组中, 代入法
和加减法有什么异同点?
(2)解方程组
