山东省滕州市张汪中学2019-2020学年度第二学期九年级数学周末拓展提高练习(第13周)(无答案)
文档属性
| 名称 | 山东省滕州市张汪中学2019-2020学年度第二学期九年级数学周末拓展提高练习(第13周)(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 214.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 00:00:00 | ||
图片预览


文档简介
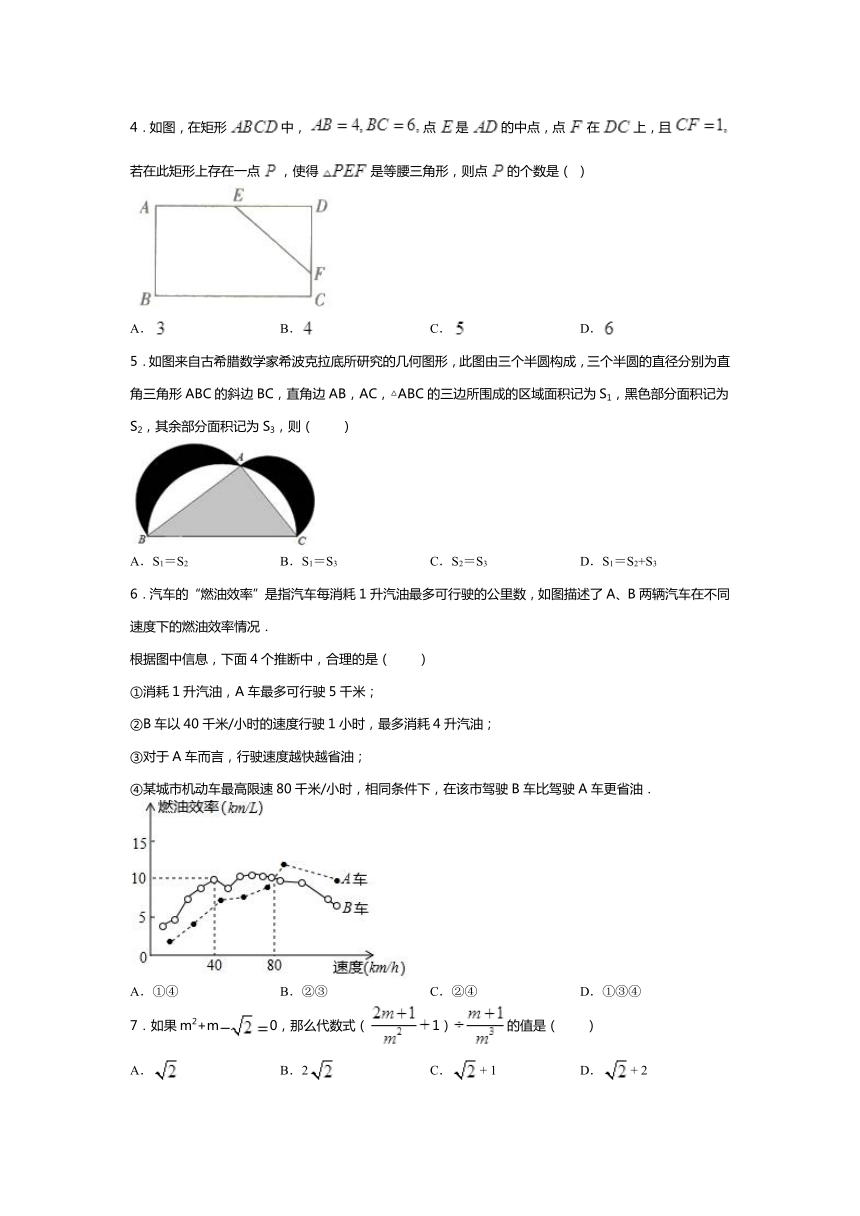
2019-2020学年度山东省滕州市张汪中学第二学期周末拓展提高练习
九年级数学(第13周)
一、单选题
1.若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是()
A. B. C. D.
2.如图,将边长为cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动8次后,正方形的中心O经过的路线长是(???)cm.
A.8 B.8 C.3π D.4π
3.如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)(???)
A.46.7m B.46.8m C.53.5m D.67.8m
4.如图,在矩形中,点是的中点,点在上,且若在此矩形上存在一点,使得是等腰三角形,则点的个数是(?)
A. B. C. D.
5.如图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域面积记为S1,黑色部分面积记为S2,其余部分面积记为S3,则( )
A.S1=S2 B.S1=S3 C.S2=S3 D.S1=S2+S3
6.汽车的“燃油效率”是指汽车每消耗1升汽油最多可行驶的公里数,如图描述了A、B两辆汽车在不同速度下的燃油效率情况.
根据图中信息,下面4个推断中,合理的是( )
①消耗1升汽油,A车最多可行驶5千米;
②B车以40千米/小时的速度行驶1小时,最多消耗4升汽油;
③对于A车而言,行驶速度越快越省油;
④某城市机动车最高限速80千米/小时,相同条件下,在该市驾驶B车比驾驶A车更省油.
A.①④ B.②③ C.②④ D.①③④
7.如果m2+m0,那么代数式(1)的值是( )
A. B.2 C.+ 1 D.+ 2
8.如图,在菱形中,,,点是这个菱形内部或边上的一点,若以点,,为顶点的三角形是等腰三角形,则,(,两点不重合)两点间的最短距离为(????)
A. B. C. D.
9.如图,点在圆上,若弦的长度等于圆半径的倍,则的度数是(??? ).
A.22.5° B.30° C.45° D.60°
10.如图,点在反比例函数的图象上,点在反比例函数的图象上,点在轴的正半轴上,则平行四边形的面积是(???)
A.6 B.5 C.4 D.3
11.抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:
x … –2 –1 0 1 2 …
y … 0 4 6 6 4 …
?
从上表可知,下列说法错误的是
A.抛物线与x轴的一个交点坐标为(–2,0) B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0 D.抛物线在对称轴左侧部分是上升的
12.如图所示在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,……,组成一条平滑的曲线,点P从原点O出发沿这条曲线向右运动,速度为每秒个单位长度,则第2019秒时,点P的坐标是( )
A.(2018,0) B.(2019,1) C.(2019,﹣1) D.(2020,0)
二、填空题
13.设是一元二次方程的两个根,且,则_____.
14.如图,在中,是半径,弦,为上一点,连接、、,若,则_____.
15.如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为______.
16.在平面直角坐标系中,已知反比例函数的图象在第一、三象限内,若该反比例函数的图象与直线有一交点且则实数________________.
17.如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是_____.
18.如图,正方形ABCD的边长为2,正方形的边长为,点在线段DG上,则BE的长为__________.
19.如图,有一个底面直径与杯高均为的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈才能将液体倒出,则此时杯子最高处距离桌面________.(,,)
20.如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.
三、解答题
21.如图,为了测量建筑物的高度,小明在点处分别测出建筑物顶端的仰角,,在点处分别测出建筑物顶端的仰角,.已知建筑物的高度为,求建筑物的高度(精确到0.1m).(参考数据:,,.)
22.如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求n和b的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
23.如图,内两条互相垂直的弦(不是直径)相交于点连接过点作于点.过点作的切线交的延长线于点.
求证:.
若求的长.
24.如图,在四边形中,对角线,交于点,,,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形.
(2)若,,求的长.
25.如图,已知抛物线y=ax2﹣3x+c与y轴交于点A(0,﹣4),与x轴交于点B(4,0),点P是线段AB下方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点的坐标;
(2)当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;
(3)当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大
九年级数学(第13周)
一、单选题
1.若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是()
A. B. C. D.
2.如图,将边长为cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动8次后,正方形的中心O经过的路线长是(???)cm.
A.8 B.8 C.3π D.4π
3.如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)(???)
A.46.7m B.46.8m C.53.5m D.67.8m
4.如图,在矩形中,点是的中点,点在上,且若在此矩形上存在一点,使得是等腰三角形,则点的个数是(?)
A. B. C. D.
5.如图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域面积记为S1,黑色部分面积记为S2,其余部分面积记为S3,则( )
A.S1=S2 B.S1=S3 C.S2=S3 D.S1=S2+S3
6.汽车的“燃油效率”是指汽车每消耗1升汽油最多可行驶的公里数,如图描述了A、B两辆汽车在不同速度下的燃油效率情况.
根据图中信息,下面4个推断中,合理的是( )
①消耗1升汽油,A车最多可行驶5千米;
②B车以40千米/小时的速度行驶1小时,最多消耗4升汽油;
③对于A车而言,行驶速度越快越省油;
④某城市机动车最高限速80千米/小时,相同条件下,在该市驾驶B车比驾驶A车更省油.
A.①④ B.②③ C.②④ D.①③④
7.如果m2+m0,那么代数式(1)的值是( )
A. B.2 C.+ 1 D.+ 2
8.如图,在菱形中,,,点是这个菱形内部或边上的一点,若以点,,为顶点的三角形是等腰三角形,则,(,两点不重合)两点间的最短距离为(????)
A. B. C. D.
9.如图,点在圆上,若弦的长度等于圆半径的倍,则的度数是(??? ).
A.22.5° B.30° C.45° D.60°
10.如图,点在反比例函数的图象上,点在反比例函数的图象上,点在轴的正半轴上,则平行四边形的面积是(???)
A.6 B.5 C.4 D.3
11.抛物线y=–x2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表所示:
x … –2 –1 0 1 2 …
y … 0 4 6 6 4 …
?
从上表可知,下列说法错误的是
A.抛物线与x轴的一个交点坐标为(–2,0) B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0 D.抛物线在对称轴左侧部分是上升的
12.如图所示在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,……,组成一条平滑的曲线,点P从原点O出发沿这条曲线向右运动,速度为每秒个单位长度,则第2019秒时,点P的坐标是( )
A.(2018,0) B.(2019,1) C.(2019,﹣1) D.(2020,0)
二、填空题
13.设是一元二次方程的两个根,且,则_____.
14.如图,在中,是半径,弦,为上一点,连接、、,若,则_____.
15.如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为______.
16.在平面直角坐标系中,已知反比例函数的图象在第一、三象限内,若该反比例函数的图象与直线有一交点且则实数________________.
17.如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是_____.
18.如图,正方形ABCD的边长为2,正方形的边长为,点在线段DG上,则BE的长为__________.
19.如图,有一个底面直径与杯高均为的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈才能将液体倒出,则此时杯子最高处距离桌面________.(,,)
20.如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.
三、解答题
21.如图,为了测量建筑物的高度,小明在点处分别测出建筑物顶端的仰角,,在点处分别测出建筑物顶端的仰角,.已知建筑物的高度为,求建筑物的高度(精确到0.1m).(参考数据:,,.)
22.如图,已知反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)求n和b的值;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
23.如图,内两条互相垂直的弦(不是直径)相交于点连接过点作于点.过点作的切线交的延长线于点.
求证:.
若求的长.
24.如图,在四边形中,对角线,交于点,,,平分,过点作交的延长线于点,连接.
(1)求证:四边形是菱形.
(2)若,,求的长.
25.如图,已知抛物线y=ax2﹣3x+c与y轴交于点A(0,﹣4),与x轴交于点B(4,0),点P是线段AB下方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点的坐标;
(2)当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;
(3)当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大
同课章节目录
