人教B版(2019)高中数学必修三第8章第二节两角和与差的余弦课件(15张PPT)
文档属性
| 名称 | 人教B版(2019)高中数学必修三第8章第二节两角和与差的余弦课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 879.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
第八章 向量的数量积与三角恒等变换
8.2.1 两角和与差的余弦
复习
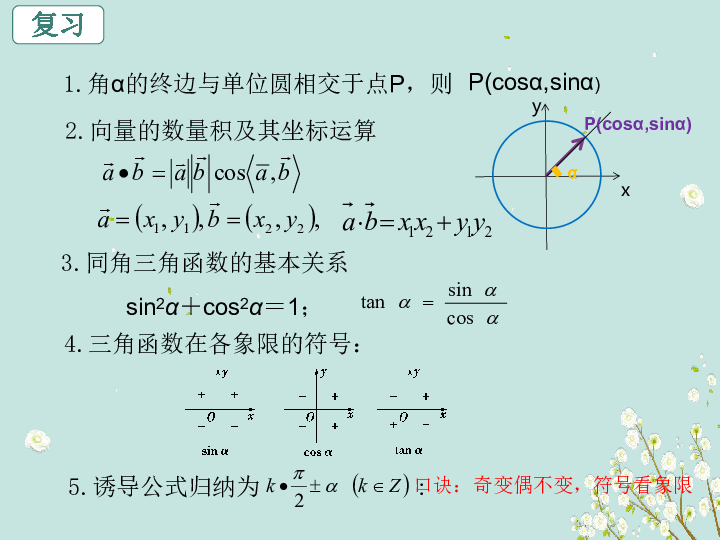
1.角α的终边与单位圆相交于点P,则
x
y
α
P(cosα,sinα)
sin2α+cos2α=1;
4.三角函数在各象限的符号:
P(cosα,sinα)
3.同角三角函数的基本关系
2.向量的数量积及其坐标运算
5.诱导公式归纳为 :
口诀:奇变偶不变,符号看象限
尝试与发现
(1)我们已经知道了30°,45°的正弦,余弦值,那么,能否根据这些之去求出cos15°的值呢?
(2)一般地,怎么根据α与β的三角函数值求出cos(α-β)的值?
因为15°=45°-30°,所以cos15°=cos(45°-30°),因此猜想
cos15°=cos45°-cos30° = <0
又因为cos15°>0, 与上述结果相矛盾,上述猜想不成立。
由此可得,对于任意角α与β,cos(α-β)=cosα-cosβ 是不成立的。
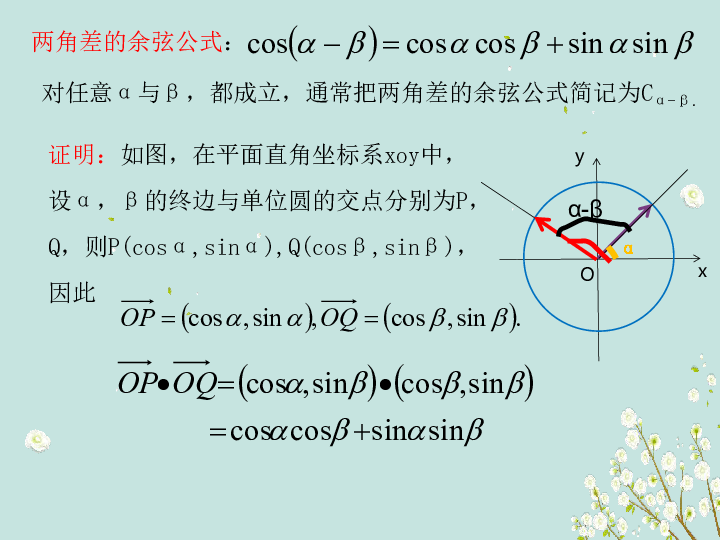
两角差的余弦公式:
对任意α与β,都成立,通常把两角差的余弦公式简记为Cα-β.
证明:如图,在平面直角坐标系xoy中,
设α,β的终边与单位圆的交点分别为P,Q,则P(cosα,sinα),Q(cosβ,sinβ),因此
x
y
α
α-β
O
x
y
α
α-β
O
例1
证明:
注意:诱导公式是两角和与差的三角函数公式的特殊情况。α,β中若有 的整数倍角时,使用诱导公式更灵活。
证明:
因为α+β=α+(-β),所以
cos(α+β)=cos[α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ
换元的思想将“+β”换成“-(-β)”用Cα+β证。
法二:
x
y
α
P1(cosα,sinα)
-β
P2(cosβ,-sinβ)
法一:
注意:(1)公式中的α,β都是任意角,即可是一个角,也可是几
个角的组合.
(2)要注意公式的正用、逆用.
(3)公式结构特征:余余正正符号相反.
符号相反
符号相反
例2
解:
非特殊角拆分成
两个特殊角的和或差再套用公式
化简求值训练
求下列各式的值
(1) (2)
(3)sin 460°sin(-160°)+cos 560°cos(-280°).
解:
(2)
(1)
(3)原式=-sin(360°+100°)sin160°+cos(360°+200°)cos280°
=-sin100°sin160°+cos200°cos280°
=-sin(180°-80°)sin(180°-20°)+cos(180°-20°)cos(360°-80°)
=-sin80°sin20°-cos20°cos80°=-cos60°=
非特殊角转化为特殊角的和或差
例3
解:
变式思考
答案:
例4
解:
逆用公Cα+β式
拓展:
解:
选择A
公式逆用,变角,多个角变成两个角
提升训练
D
解:
根据已知三角函数值判断角的范围
未知角拆分成与已知角有关的角和或差
对公式C(α-β)和C(α+β)的说明 (1)公式的结构特点:“余余正正,加减相反”. (2)公式的适用条件:公式中的α,β不仅可以是任意具体的角,也可以是一个“团体”.
课堂小结
下课了
第八章 向量的数量积与三角恒等变换
8.2.1 两角和与差的余弦
复习
1.角α的终边与单位圆相交于点P,则
x
y
α
P(cosα,sinα)
sin2α+cos2α=1;
4.三角函数在各象限的符号:
P(cosα,sinα)
3.同角三角函数的基本关系
2.向量的数量积及其坐标运算
5.诱导公式归纳为 :
口诀:奇变偶不变,符号看象限
尝试与发现
(1)我们已经知道了30°,45°的正弦,余弦值,那么,能否根据这些之去求出cos15°的值呢?
(2)一般地,怎么根据α与β的三角函数值求出cos(α-β)的值?
因为15°=45°-30°,所以cos15°=cos(45°-30°),因此猜想
cos15°=cos45°-cos30° = <0
又因为cos15°>0, 与上述结果相矛盾,上述猜想不成立。
由此可得,对于任意角α与β,cos(α-β)=cosα-cosβ 是不成立的。
两角差的余弦公式:
对任意α与β,都成立,通常把两角差的余弦公式简记为Cα-β.
证明:如图,在平面直角坐标系xoy中,
设α,β的终边与单位圆的交点分别为P,Q,则P(cosα,sinα),Q(cosβ,sinβ),因此
x
y
α
α-β
O
x
y
α
α-β
O
例1
证明:
注意:诱导公式是两角和与差的三角函数公式的特殊情况。α,β中若有 的整数倍角时,使用诱导公式更灵活。
证明:
因为α+β=α+(-β),所以
cos(α+β)=cos[α-(-β)]
=cosαcos(-β)+sinαsin(-β)
=cosαcosβ-sinαsinβ
换元的思想将“+β”换成“-(-β)”用Cα+β证。
法二:
x
y
α
P1(cosα,sinα)
-β
P2(cosβ,-sinβ)
法一:
注意:(1)公式中的α,β都是任意角,即可是一个角,也可是几
个角的组合.
(2)要注意公式的正用、逆用.
(3)公式结构特征:余余正正符号相反.
符号相反
符号相反
例2
解:
非特殊角拆分成
两个特殊角的和或差再套用公式
化简求值训练
求下列各式的值
(1) (2)
(3)sin 460°sin(-160°)+cos 560°cos(-280°).
解:
(2)
(1)
(3)原式=-sin(360°+100°)sin160°+cos(360°+200°)cos280°
=-sin100°sin160°+cos200°cos280°
=-sin(180°-80°)sin(180°-20°)+cos(180°-20°)cos(360°-80°)
=-sin80°sin20°-cos20°cos80°=-cos60°=
非特殊角转化为特殊角的和或差
例3
解:
变式思考
答案:
例4
解:
逆用公Cα+β式
拓展:
解:
选择A
公式逆用,变角,多个角变成两个角
提升训练
D
解:
根据已知三角函数值判断角的范围
未知角拆分成与已知角有关的角和或差
对公式C(α-β)和C(α+β)的说明 (1)公式的结构特点:“余余正正,加减相反”. (2)公式的适用条件:公式中的α,β不仅可以是任意具体的角,也可以是一个“团体”.
课堂小结
下课了
