2020年中考数学运动型问题例谈专题复习学案(习题无答案)
文档属性
| 名称 | 2020年中考数学运动型问题例谈专题复习学案(习题无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 16:09:11 | ||
图片预览




文档简介
2020年中考数学专题复习和训练:
运动型问题例谈
专题透析:
初中数学的运动型问题一般是指几何动态问题,主要是研究几何图形运动变化过程中的数学关系和规律,往往要调动多种数学知识来使问题得以解决,其中渗透了转化、分类讨论、整体、方程、函数、数形结合以及数学建模等思想方法,是近年来各地数学中考的热点题型,从自贡市17、18、19三年的数学中考来看,每套中考试题至少都有两三道运动型的题.运动型问题包含点、线、三角形、四边形以及函数图象等的动态变化,其中动点问题最多.运动型问要注意从以下几个方面解决问题:首先弄清运动方式和形式;其次注意分类讨论,画出相应图形,化动为静;再次运用数学知识以及思想方法探索关系,建模解答.下面我精选了一部分运动型的精典题型进行分析、解答和点评,并附有追踪练习和巩固提升练习,希望对同学们迎考有所帮助.
典例精析:
题目一.几何图形中的动点问题典例
例1. 正方形的边长为8,在上,且,是上一动点,则的最小值为 ( )
A. B. C. D.
分析:
要在直线上找一点,使此点到直线同旁的两个已知定点的距离之和最小,根据轴对称和“两点之间,线段最短”,就是要作出其中一定点的对称点,连对称点与另一定点的连线得到与已知直线的交点,化动为静,再利用相关知识解答.
如图,连接,根据正方形轴对称的性质可知点关于对角线
对称;再连接与对角线的交点就是使有最小值的点.
根据正方形轴对称和线段垂直平分线的性质可知:
∴ .
在△中, ,,
∴ ,即的最小值为10;故选D.
点评:
本题可以视为“单动点运动型”的题型,关键是找找出符合条件的那个点的位置;就满足“距离之和最小值”的这种题型要求的点,第一步关键是找出定点关于直线的对称点,有的对称点要作垂线,截取相等找出来;有的对称点是现成的,比如等腰三角形、特殊四边形、圆以及抛物线等等,一般可以直接连接起来;这类题容易与勾股定理串联解决问题.
例2. 在矩形中,,点从点开始以
的速度沿边向点移动,点从点开始以的速度沿边向点
移动,如果分别从同时出发,几
秒后△的面积等于 ?
分析:
△的面积可以由其两直角边乘积的一半表示(见下面的分析图标示),而可以由时间表示,以此建立方程后问题
可解决.
解:设秒后△的面积等于,则根据题意列方程:
整理为
解得:
∵,∴均符合题意.
故不合题意舍去.
答:设2秒或4秒后△的面积等于.
点评:
本题可以视为“双动点运动型”的题型.1.关键:以静代动,化动为静.把动的点进行转换,变为线段的长度2.方法:时间变路程.求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;3.常用的数量关系:面积,勾股定理等.
例3.(2019-2020上.自贡统考)如图,是⊙的直径,为圆上一
点,且; ⊙的半径为2,为圆上一动点,为的
中点,则的长的最值是 .
考点:点的轨迹,勾股定理。圆的有关性质等.
解析:
根据题意可知中点的运动轨迹是以为直径的圆(见图中的红色部分),最长或最短都是在过轨迹圆的圆心的直线上来探讨,见图中最长,最短.
如图,过作于点,则 ;
∵ ,且
∴
∴
在△中根据勾股定理有: ;
在△中根据勾股定理有:,解得:.
∴,.
故应填:.
点评:
本题看起来似乎有两个动点,但中点是受动点控制的,相对于点来说,动点是个“半自由点”.本题分析出线段中点的运动轨迹是一个圆,其次结合“直径是圆内最长的弦”来求的最值是本题破题的关键;本题渗透了高中数学的运动轨迹,体现了新教材与高中数学知识相衔接的特点,也是命题的新方向;本题对数学学习有一定的导向作用.
例4.(2018.自贡中考) 如图,在⊿中,,将它沿翻折得到⊿,则四边形的形状是 形,点分别为线段的任意点,则的最小值是 .
考点:菱形、轴对称、等腰三角形的性质,两点之间线段最短,垂线段最短,勾股定理,菱形面积等
分析:
翻折前后两个部分就是成轴对称的.再加上,可以推出,所以四边形的形状是菱形.
关于求的最小值:
方法一.本题关键是不是定点,而是动点;仍然可以先作关于线段的对称点 , 连接 ,再将移动使,因为“垂线段最短”.再根据轴对称的性质可得到;实际上此时的点恰好是的中点. 就是菱形一边上的高,可把平移成等腰⊿腰上的高来解决.见下面的分析流程图组图I.
见下面组图1最后一个图,过作于,连接;
∵,是的中点 ;
∴;在⊿中有
∴ ;
根据面积公式可知⊿=
∴ , 解得 ;
易证
∴ . 故应填.
方法二.大家都知道从等腰三角形底边上的任何一点向该三角形两腰作垂线段,两垂线段的和是个恒值,且等于等腰三角形一腰上的高.所以直接过点向菱形的两邻边边垂线段,因为“垂线段最短”,所以与之和便最小,然后也把转化成等腰三角形一腰的高的高来解决,见下面流程组图2,同样可以(计算略).两种方法的计算量是一样的.
点评:
本题告诉的三个任意点都是动点,可以视为“多动点运动型”的题型;本题可以把其中一个点作为定点切入思考,有两条思路;一是除了要注意利用轴对称知识、“两点之间,线段最短.”,其次还结合“垂线段最短”来求出最小值,就是在变化中寻找“不变”的部分.本题是一道高质量的中考题.
追踪练习:
1.如图,菱形中,,点是边的中点,点
是对角线上的一个动点;若的最小值是,则
的长为 ( )
A. B. C. D.
2.正方形的边长为8,在上,且,是上
一动点,则的最小值为 ( )
A. B. C. D.
3. 如图,点是⊙ 上直径所分的半圆的一个三等分点,点是
弧的中点,点是上一动点,⊙的半径为3,则的
最小值为________.
4.在等腰△中,,,为底边上一动点
(不与点中和),,垂足分别为,则
= .
5.在边长为的正方形中,点为边的中点,为对角线上一动点;连接,则△周长的最小值为 .
6.如图,已知四边形,∥,,
;;点从出发以的速度沿折线
方向运动;点从出发,以的速度沿线段
向运动;若动点同时出发,当点到达后,同时停
止运动; 则经过 秒时,四边形是平行四边形. 此
时它的周长为 .
7.如图,在△中,;是的中点,点分别在边上运动,但始终保持, 连接.
⑴.求证:△≌△;
⑵.试证明△是等腰三角形.
8.如图,在△中,,于点,且,是的中点.
⑴.线段= ;
⑵.连接 ,求证:四边形是菱形;
⑶.动点从点以2个单位每秒2个单位长度沿运动,经
过多少时间,△是直角三角形.
9.如图,已知矩形的对角线交于点,;设,.
⑴.求矩形的面积;
⑵.点是矩形的边上的一动点(点不与重
合),过点作,垂足分别为;
求的值.
10.如图,等腰直角△中,,动点从点出发,沿向移动,通过点引平行于,的直线与,分别交于;当等于多少厘米时,平行四边形的面积等于 ?
11. 如图,在菱形中,交于点,,动
点从点出发沿方向以匀速直线运动到,动点从
点出发沿方向以匀速直线运动到点;若点同
时出发,问出发后几秒钟时,的面积为?
12.如图,⊿中,点是边上的一个动点,过点作直线∥ ;设交的平分线于点,交的外角平分线于点.
⑴.判断与的大小关系?并说明理由?
⑵.当点运动到的何处时,四边形是
矩形?并说出你的理由.
13.如图所示,在菱形中,,△为正三角形,点分别在菱形的边上滑动,且不与重合.
⑴.证明不论在如何滑动,总有;
⑵.当点在上滑动时,分别探讨四边形和
△的面积是否发生变化?如果不变,求出这个定值;如果
变化,求出最大(或最小)值.
14.如下图,以等腰△的一腰为直径的⊙交于,过作于
试证:是⊙的切线
问:
⑴.若点在上向移动,以为圆心,以为半径的圆仍交于,的条件不变,那么上述结论是否还成立?请说明理由;
⑵.如果,,那么圆心在上什么位置时,⊙与相切?
题目二.函数题型中动点问题典例
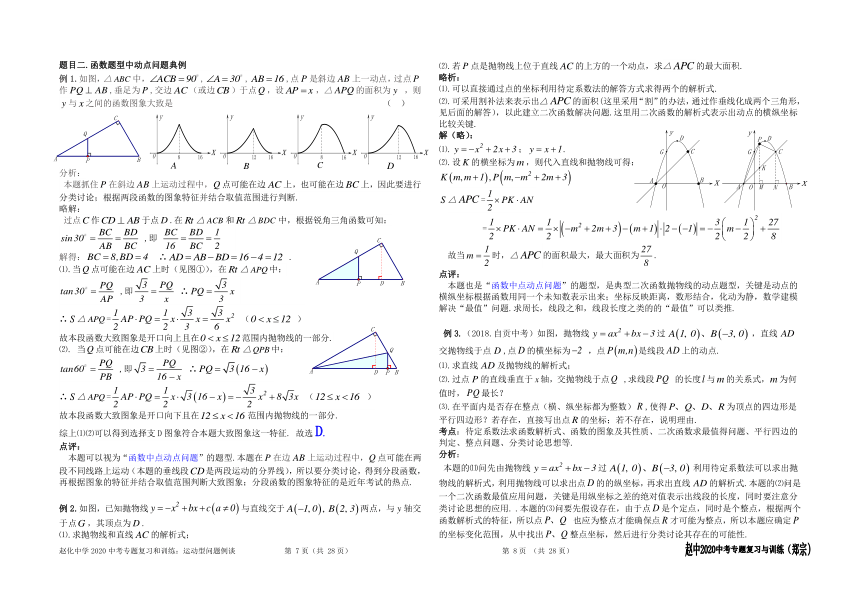
例1.如图,△中,,,,点是斜边上一动点,过点作,垂足为,交边(或边)于点,设,△的面积为 ,则与之间的函数图象大致是 ( )
分析:
本题抓住在斜边上运动过程中,点可能在边上,也可能在边上,因此要进行分类讨论;根据两段函数的图象特征并结合取值范围进行判断.
略解:
过点作于点.在△和△中,根据锐角三角函数可知: ,即
解得: ∴ .
⑴.当点可能在边上时(见图①),在△中:
,即 ∴
∴△= ( )
故本段函数大致图象是开口向上且在范围内抛物线的一部分.
⑵. 当点可能在边上时(见图②),在△中:
,即 ∴
∴△= ( )
故本段函数大致图象是开口向下且在范围内抛物线的一部分.
综上⑴⑵可以得到选择支D图象符合本题大致图象这一特征. 故选D.
点评:
本题可以视为“函数中点动点问题”的题型.本题在在边上运动过程中,点可能在两段不同线路上运动(本题的垂线段是两段运动的分界线),所以要分类讨论,得到分段函数,再根据图象的特征并结合取值范围判断大致图象;分段函数的图象特征的是近年考试的热点.
例2.如图,已知抛物线与直线交于两点,与轴交于点,其顶点为.
⑴.求抛物线和直线的解析式;
⑵.若点是抛物线上位于直线的上方的一个动点,求△的最大面积.
略析:
⑴.可以直接通过点的坐标利用待定系数法的解答方式求得两个的解析式.
⑵.可采用割补法来表示出△的面积(这里采用“割”的办法,通过作垂线化成两个三角形,见后面的解答),以此建立二次函数解决问题.这里用二次函数的解析式表示出动点的横纵坐标比较关键.
解(略):
⑴.;.
⑵.设的横坐标为,则代入直线和抛物线可得:
△=
=
故当时,△的面积最大,最大面积为.
点评:
本题也是“函数中点动点问题”的题型,是典型二次函数抛物线的动点题型,关键是动点的横纵坐标根据函数用同一个未知数表示出来;坐标反映距离,数形结合,化动为静,数学建模解决“最值”问题.求周长,线段之和,线段长度之类的的“最值”可以类推.
例3.(2018.自贡中考)如图,抛物线过,直线交抛物线于点,点的横坐标为 ,点是线段上的动点.
⑴.求直线及抛物线的解析式;
⑵.过点的直线垂直于轴,交抛物线于点 ,求线段 的长度与的关系式,为何值时,最长?
⑶.在平面内是否存在整点(横、纵坐标都为整数),使得为顶点的四边形是平行四边形?若存在,直接写出点的坐标;若不存在,说明理由.
考点:待定系数法求函数解析式、函数的图象及其性质、二次函数求最值得问题、平行四边的判定、整点问题、分类讨论思想等.
分析:
本题的⑾问先由抛物线过利用待定系数法可以求出抛物线的解析式,利用抛物线可以求出点的的纵坐标,再求出直线的解析式.本题的⑵问是一个二次函数最值应用问题,关键是用纵坐标之差的绝对值表示出线段的长度,同时要注意分类讨论思想的应用. .本题的⑶问要先假设存在,由于点是个定点,同时是个整点,根据两个函数解析式的特征,所以点 也应为整点才能确保点才可能为整点,所以本题应确定的坐标变化范围,从中找出整点坐标,然后进行分类讨论其存在的可能性.
略解:
⑴.∵抛物线过
∴ 解得: 所以
∵点的横坐标为
∴当 时, ∴
设直线 的解析式为
∵
∴ 解得 所以
⑵. ∵点,过点的直线垂直于轴,交抛物线于点.
∴点和点的横坐标相等.
当时代入得:;则点.
当时代入得:.则点.
∴ 即
①.当时,;整理
∵ ∴当 时,有最大值;即此时线段最长.
②.当时,;整理
∵ ∴此时有最小值;不合本问题意,舍去.(根据题中条件,本情况可不讨论)
综上所述:当 时,线段最长.
⑶.在平面内存在整点(横、纵坐标都为整数),使得为顶点的四边形是平行四边形. 整点坐标分别为: .
因为是线段上的动点,计算出,从而确定点横纵坐标的变化范围进行整点坐标的分类讨论(根据解析式和点的坐标,点 也应为整点).
①.当时,;以作为定点,能使点与它们构成平行四边(分别以 为边和对角线讨论)的整点坐标情况有: (见分析示意图①).
②.当时,;以作为定点,能使点与它们构成平行四边(分
别以 为边和对角线讨论)的整点坐标情况有: (见分析示意图②).
注:当点与 重合时,点点也同时会相应的与 重合时,该四边形不存在.
综上所述,满足条件的整点的坐标有.
点评:
本题主要⑴问求出点的坐标后,用待定系数法可以求出两个函数的解析式,比较简单!在函数的相关题型中,求“最值”问题,常通过建立二次函数的模型来解;本题⑵问就是抓住长度等于纵坐标之差的绝对值建立二次函数来解决,注意讨论.本题以为顶点的四边形顶点有3个动点,是本问的难点所在,结合解析式和其中一个顶点是定点且为整点,把动点中的 也视为“定点”,化动为静,在此基础上讨论就比较容易破题了.
追踪练习:
1.如图①,矩形中,动点从点出发,沿匀速运动至点,设点运动的路程为,的面积为,如果关于的函数图象如图②所示,的面积是 ( )
A.10 B .16 C.18 D.20
2.在边长为的正方形中,对角线与相交于点,是上的一动点,过作∥,分别交正方形的两条边于;设,的面积为,则能反映与的函数关系的图象为 ( )
3. 如图,△中,,是上的一动点;过点作于点,设 ,△的面积为,则与之间的关系图象大致为( )
4.如图,正方形中,,对角线与相交于点,点分别从两点同时出发,以的速度沿运动,到点停止运动.设运动时间为,⊿的面积为与的函数关系式可用图象表示为 ( )
5.如图,已知矩形的长为5,宽为4; 是边上的
一个动点, ,交于点;设,则点
从点运动到点时,能表示是的函数关系的大致图象是 ( )
6.已知反比例函数的图象如图 ,点是
反比例函数的一个动点,连接,过点作
于点,则点在运动过程中, 的大小的变化趋势为 ( )
A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变
7. 如图,点为直线的一动点,动点在轴上,始终
保持;若△,则点的坐标为 .
8.如图,抛物线与轴的交点为,点的坐标为;点是抛物线上的一个动点;若△是以为底边的等腰三角形,则点
的坐标为 .
9.如图,在△中, , ;动点从
点开始沿向以的速度移动(不与点 重合),动点
从点开始沿 以的速度移动(不与点重合).如果
分别从同时出发,那么经过 秒,四边形的面积最小.
10.如图,直线交轴、轴于两点,点是双
曲线的图象上的一点;轴于点, 轴
于点 ,交直线于两点,则= .
11.如图,直线与轴、轴分别交于两点.
⑴.求点的坐标;
⑵.点是直线上的一个动点,试写出⊿
的面积与的函数关系式;
⑶.探究:
①.当点运动到什么位置时,⊿的面积为,并说明理由.
②.在①成立的情况下,轴上是否存在点,使⊿是等腰三角形;
若存在,请直接写出满足条件的所有的坐标;若不存在,请说明理由.
12.在矩形中,,点从点开始以的速度沿边向点移动,点从点开始以的速度沿边向点移动,如果分别从同时出发
⑴.若设点运动的时间为,△的面积为,求出与之间
的函数关系式;
⑵.在题中条件下几秒后△的面积最大,最大面积是多少?
13..如图,已知二次函数的图象与轴交于两点,是抛物线与轴的交点,点是线段上的动点,过点作轴的垂线与抛物线相交于点,四边形的面积有最大值吗?如果有,最大值是多少?并求出此时点的坐标.
14.如图,已知抛物线与坐标轴交于三点,且点的坐标为.
⑴.求抛物线的解析式及两点的坐标;
⑵.为抛物线上之间的一点,为线段上一点,若∥轴,求的最大值.
15.如图,在平面直角坐标系中,抛物线经过三点,已知点.
⑴.求此抛物线的解析式;
⑵.点是直线上方的抛物线上一动点(不与重合),过点作轴的垂线,垂足为点,交直线于点,作于.
①.动点 在什么位置时,△的周长最大,求出此时点的坐标;
②.连接,以为百年作图示一侧的正方形,随着点的的运动,正方形的大小、位置也随之改变,当顶点或恰好落在抛物线的对称轴上时,求此时对应的点的坐标.(结果保留根号)
题目三.其他运动型问题举例
例1. 如图,△放在直角坐标系内,其中,点
的坐标分别为,将△沿轴向右平移,当点落
在直线上时,线段扫过区域面积为 .
考点:利用点的坐标求距离、利用函数求坐标、平移的特征、勾股定理、平行四边形的面积.
分析:根据题意可知线段扫过区域构成一个平行四边形,求平行四边
形的面积可以由底乘以高得到,底的长度可以由平移的距离获得,高
可以由求得. 化在△中由勾股定理求出,求的长度关
键是求的坐标,由于在直线上,而是由沿轴向右
平移得到的,所纵坐标可由的长度来确定,以此代入求
出,从而进一步求出的长度.
略解:如图所示∵的坐标分别为,∴;∵
∴ ∵点平移的点落在直线 ∴ 解得:
即;∴ ∴□.
故应填写.
点评:
本题属于平移型的动态问题;本题综合了较多的基础知识点,且各知识点自然衔接,融基础性和灵活性为一体,是一道价值较高的基础综合题.本题有两个常规性解题小技巧值得总结:①.利用坐标求平移距离,若是沿坐标轴方向平移(或平行于坐标轴),平移的距离可以由横(或纵)坐标之差的绝对值求出;②.利用函数求点坐标,根据已知的横(或纵)代入解析式求纵(或横)坐标.
例2. 如下面的图,在平面直角坐标系中,将△绕点顺时针旋转到△的位置,点分别落在处,点在轴上;再将△绕着点顺时针旋转到△的位置,点在轴上;再将△绕着点顺时针旋转到△的位置,点在轴上;…;依次进行下去.若点,则的坐标为 .
分析:
根据已知坐标并结合勾股定理可以求出三边的长,根据旋转可以计算出偶数序号点之间相差的距离单位数,当然也可以算出奇数序号点之间相差的距离单位数;本题序号符合前者特征,所以根据偶数序号横纵坐标的坐标变化规律就可以推算出的横坐标.
略解:∵
∴
∴
∴的横坐标为10.
又
∴的坐标为
同样可以计算出(即横坐标是的10倍,纵坐标均为4)
∴的横坐标为
∴的坐标为.
故应填:.
点评:
本题属于连续转转但每次旋转中心都在发生变化(也就是翻转)的运动型问题;这类题主要是根据旋转计算出横纵坐标的变化规律;就本题而言偶数序号点的横坐标每相邻两个之间相差10,纵坐标均为4;奇数序号点的开始横坐标每相邻两个之间相差10,纵坐标均为.本题符合前者规律,根据规律可以计算得出答案.
例3.如图,在矩形中,,是边的中点,是线段边上的动点,将△沿所在直线折叠得到△,连接,则的最小值是 ( )
A. B.6 C. D.4
略析:连接.
∵是边的中点 ∴
在△根据勾股定理易求.
又根据翻折对称的性质可知
∴△中两边一定,要使的长度最小即要使最小(也就是使其角度为0°),此时点落在上(如图所示).
∵根据翻折即轴对称可知
∴
∴的长度最小值为.
点评:
本题属于动点和翻折相结合的复合运动型问题.首先主要找到动点要运动符合条件的“特殊点位”,然后结合翻折即轴对称的性质来解决问题,与翻折问题相关的计算常常需要勾股定理.
追踪练习:
1.如图,将周长为8的△沿方向平移1个单位得到△,则四边形的周长等于 ( )
A.8 B.9 C.10 D.11
2.如图,将边长为的正方形纸片沿其对角线
剪开,再把△沿着方向平移,得到△,若两
个三角形重叠部分(见图中阴影)的面积为,则它移动
的距离等于 ( )
A. B. C.或 D.或
3.如图,将边长为 的正方形沿对角线平移,使点至
的中点处,得到正方形,新的正方形与原正方形的重叠部
分(图中的阴影部分)的面积是 ( )
A. B. C. D.
4.如图,动点从出发,沿如图所示的方向(看图中的编
号)运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,
当点第2017次碰到矩形的边时,点的坐标为 ( )
A. B. C. D.
5.如图,水平地面上有一面积为的扇形,半径,且与地面垂直,在没有滑动的情况下,将扇形向右滚动至与地面垂直为止,则点 移动的距离为 ( )
A. B. C. D.
6.如图,有一矩形纸片, ,将纸片折叠,使边落在边上,折痕为 ,再将⊿以为折痕向右折叠,与 交于点,则的面积为 ( )
A.4 B.6 C.8 D.10
7. 如图.矩形纸片中,已知 ,折叠纸片使边与对角线重合,点落在点处,折痕为,且,.则的长为 ( )
A.3 B.4 C.5 D.6
8. 如图,边长为1的正方形绕点逆时针旋转30°到正方形, 图中的阴影部分的面积为 ( )
A. B. C. D.
9.四边形中,∥,,将腰绕点
顺时针旋转90°至,则图中阴影部分的面积是 ( )
A.1 B.2 C.3 D.4
10.如图,将边长为1的正方形沿轴正方向连
续翻转8次,点依次落在点 ,则
点的横坐标是 ( )
A.5 B.6 C.7 D.9
11.如图,在平面直角坐标系中,,把
一条长2020个单位长度的且没有弹性的细线(线的粗细忽略不计)的一
端固定在点,并按 的规律绕在四边形
上,则细线的另一端所在位置的点的坐标是 .
12.如图,一段抛物线记为,
它与轴的交点为,顶点为;将绕点旋转
180°得到,交轴于点为,顶点为;将绕
点旋转180°得到,交轴于点为,顶点为
;……,如此进行下去,直至到,顶点为,
则顶点的坐标为 .
13.如图所示,已知.将绕点旋转150°
后,得到,此时点的对应点的坐标为 .
14.如图,将边长为的正六边形在直线上由图1的位置按顺时针方向作无滑动滚动,当第一次滚动到图2位置时,顶点所经过
的路径的长为 .
15.将两张长均为8cm,宽均为2cm的矩形纸条按如图交叉叠放.
16.重叠部分是一个什么样的四边形?
⑵.将其中一张纸条不动,另一张纸条转动,什么情况下重叠部分的周长和面积最小,什么情况下最大?并求出此时重叠部分周长和面积最小值和最大值分别是多少?
17.按下列折叠进行解答:
⑴.如图,矩形纸片中,,将纸片折叠,使顶点落在边的点上,折痕的一端点在边上, .
①.当折痕的另一端点在边上时,如图①,求⊿的面积;
②.当折痕的另一端点在边上时,如图②,证明四边形为菱形,并求出折痕的长.
⑵.在矩形纸片中,.如图③所示,折叠纸片,使点落在边上的处,折痕为 ,当点在边上移动时,折痕的端点也随之移动.若限定点分别在边上移动,求点在边上可移动的最大距离.
18.如图①,一等腰直角三角尺的两条直角边与正方形的两条边分别重合在一起.现正方形保持不动,将三角尺绕斜边的中点(点也是中点)按顺时针方向旋转.
⑴.若三角尺旋转到如图②,当与相交于点,与相交于点时,通过观察或测量的长度,猜想满足的数量关系,并证明你的猜想;
⑵.若三角尺旋转到如图③所示的位置时,线段的延长线与的延长线相交于点,线段的延长线与的延长线相交于点,此时⑴中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
19.(自贡中考)如图,已知,在的平分线上有一点,将一个120°角的顶点与点重合,它的两条边分别与直线相交于点 .
⑴.当绕点旋转到与垂直时(如图1),请猜想与的数量关系,并说明理由;
⑵.当绕点旋转到与不垂直时,到达图2的位置,⑴中的结论是否成立?并说明理由;
⑶.当绕点旋转到与的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段与之间又有怎样的数量关系?请写出你的猜想,不需证明.
巩固提升练习:
1. 如图,已知四边形, 分别为上的点,
分别是的中点,当动点在上从点向点移动而点不
动时,那么下列结论成立的是 ( )
A.线段的长逐渐增大 B.线段的长逐渐减少
C.线段的长不变. D.线段的不能确定
2.如图,已知菱形在平面直角坐标系的位置如图所示,顶点, ,点是对角线上的一个动点, 当最短时,点的坐标为 ( )
A. B. C. D.
3.如图,△中,;点是边上的一个动点(点与点不重合),过点作,垂足为,点是的中点,连接;设△的面积为,点从点沿运动到点的过程中与的距离为,则与之间的关系图象大致是( )
4.如图,⊙的半径为1,是⊙互相垂直的直径,点从点出发(点与不重合) ,沿 → → 的路线运动;设,那么与之间的关系图象大致是 ( )
5. 如图在△中,,正方形的顶点分别是边的动点,两点不重合.设的长度为,△与正方形的重叠部分的面积为,则下列图象中能表示与的函数关系的是 ( )
6.(2019.达州)如图,边长都为4的正方形和正△如图放置 ,与在同一直线上,点与点重合;现将△沿方向以每秒1个单位的速度匀速运动,当点与重合时停止,在这个运动过程中,正方形和正△重叠部分的面积与运动时间的函数图象大致是 ( )
7.如图,正方形的边长为,动点从点出发,在正方形的边上沿 → → 的方向运动到点停止;设点运动的路程为,在下列图象中,能表示△的面积关于的函数关系的图象是 ( )
8.如图,已知是反比例函数图象上的两点,∥轴 ,交轴于点,动点从原点出发,沿 → → → (图中的“→”表示路线)匀速运动,终点为;过点作轴,垂足为;设△的面积为.点的运动时间为,则与运动时间的函数图象大致是 ( )
9.如图,点的坐标为,点是轴正半轴上的一动点,以为边作等腰直角三角形⊿,使,设点的横坐标为,点的纵坐标为,能表示与的函数关系的图象大致是 ( )
10.(2019.自贡)如图,已知 两点的坐标分别为,
点分别是直线和轴上的动点,,
点是线段的中点,连接交轴于点;当⊿面
积取得最小值时,的值是 ( )
A. B. C. D.
11.(2019.乐山)如图,抛物线与轴交于点,
是以点以为圆心,2为半径的圆上的动点,点是
线段的中点,连接,则线段的最大值是 ( )
A. B. C. D.
12. 如图,在△中, ,,,动点从点开始沿边向以的速度移动,,动点从点开始沿向 以的速度移动.若
分别从同时出发,在运动过程中,⊿的最大面积是 ( )
A. B. C. D.
13.如图,在在△中,,是线段上的动点(不含端点),若线段长正整数 ,则点的个数共有 ( )
A.5个 B.4个 C.3个 D.2个
14.如图,将正六边形放置在平面直角坐标系内,,点在原点,把正六边形沿轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点 的坐标是 ( )
A. B.
C. D.
15.菱形的对角线分别为12和16, 分别为的中点,是对角线上的一动点,则的最小值为 .
16.正方形的面积为,,为上的一动点;则的最小值为 .
17.如图,在⊿中,;是⊿的中位线,点是边的一点, ;点是线段上的一个动点,连接,,与相交于
点 ;若⊿是直角是直角三角形,则的长是 .
18.如图,抛物线与轴交于点,点,点是抛物线上的动点,若⊿是以为底边的等腰三角形,则点的坐标为 .
19.(2019.乐山)如图1,在四边形中, ∥,,直线沿射线方向,从点开始向右平移时,直线与四边形的边分别相交于点;设直线向右平移的距离为,线段的长为,且与的函数关系如图2所示,则四边形的周长为 .
20.如图,在平面直角坐标系中,已知点的坐标分别为,是的中点,过点作轴的垂线,垂足为;动点从点出发,沿向点匀速运动,过点作轴的垂线,垂足为,连接 ,当所在的直线与所在直线第一次垂直时,点的坐标为 .
21.如图,在平面直角坐标系中,□的顶点的坐标分别是,,动点在直线上运动,以点为圆心,长为半径的⊙随点运动,当⊙与□的边所在直线相切时,点的坐标为 .
22.如图,半径为2的⊙与含有30°角的直角三角板的边切于点,将直角三角板沿边所在的直线向左平移,当平移到与⊙相切时,该直角三角板平移的距离为 .
23.如图在四边形中, ∥, ∠;动点从点开始沿边向 以的速度运动,动点从点开始沿边向点以的速度运动,规定当其中一点到达端点时,另一点也随之停止.
⑴.从运动开始,需经过多少时间四边形是平行四边形;
⑵.从运动开始,需经过多少时间四边形中的边 .
?
24.已知矩形中,,的垂直平分线分别交于点,垂足为.
⑴.如图甲,连接.求证:四边形为菱形,并求的长;
⑵.如图乙,动点分别从出发,沿△和△各边匀速运动一周,即点自
→→→停止,点自→→→停止.在运动过程中:
①.已知点的速度每秒,点的速度每秒,运动时间为秒,当点四点为顶点的四边形是平行四边形时,求的值.
②.若点的运动路程分别为(单位:,),已知四点为顶点的四边形是平行四边形,写出与满足的数量关系.(直接写答案,不要求证明)
25. ⊿和⊿都是正三角形,.
⑴.求证:⊿≌⊿
⑵.当 运动至边上的何处时,四边形为平行四边形?
26.如图,正方形的边长为,分别是上的动点,且?
⑴.求证:四边形是正方形;??????????????????????????????
⑵.求四边形面积的最小值.?
27. 为边长为1的正方形的对角线上的一点,且,为上的一动点, ,求的值
28.已知点为正方形的中心(对角线的交点),为射线上一动点(与点不重合,以线段为一边作正方形,连结.
⑴.当点在线段上时(如图甲),线段与有怎样的关系?请说明理由.
⑵.当点在线段的延长线上时(如图乙),⑴中的结论是否仍然成立?请结合图乙说明理由.
29.如图,在边长为4的正方形的一边上,一点从点运动到点,设,四边形的面积为.
⑴.求与的函数关系式及的取值范围;
⑵.是否存在点,使四边形的面积为5.5,请解答说明.
30.矩形的周长是,设矩形的一边长为,另一边长为
⑴.求关于的函数关系式,并写出自变量的取值范围;
⑵.作出函数的图象;
⑶.若点是该图象上的一动点,点的坐标为,设△的面积为,用含的解析式表示.
31.已知矩形中,;分别是矩形的边的动点,点以/秒的速度由向匀速运动,点同时以/秒的速度由向匀速运动;若设运动的时间为(秒),四边形(图中的阴影部分)面积为.
⑴.求与的函数关系式及的取值范围;
⑵. 出发多少秒后四边形的面积为?
32.已知四边形是边长为4的正方形,以为直径在正方形内作半圆,是半圆上的动点(不与点 重合),连接.
⑴.如图①,当的长度等于 时,;当的长度等于 时,⊿是等腰三角形;
(2).如图②,以边所在直线为轴、边所在直线为轴,建立如图所示的直角坐标系(点即为原点),把⊿,⊿,⊿的面积分别记为 ,坐标为(,试求的最大值,并求出此时的值.
33.已知直线:与轴、轴分别交于点,是轴上一点,以为圆心的⊙与直线相切于点.
⑴.求点的坐标和⊙的半径;
⑵.若⊙以每秒个单位向轴负方向运动,同时⊙的半径以每秒 个单位变小,设⊙的运动时间为秒,且⊙始终与直线有公共点,试求 的取值范围;
⑶.在⑵中,设⊙被直线截得的弦长为,问是否存在的值,使值最大?若存在,求出的值;若不存在,请说明理由;
⑷.在⑵中,设与直线的一个公共点为 ,若以为顶点的三角形与⊿相似,请直接写出此时的值.
34.如图,抛物线经过⊿的三个顶点,与轴相交于点,点的坐标为,点是点关于轴对称点,点在轴的正半轴上.
⑴.求抛物线的解析式;
⑵.点为线段上一动点,过点作轴,轴,垂足分别为,当四边形为正方形时,求出的坐标;
⑶.将⑵中的正方形沿向右平移,记平移中的正方形为正方形,当点和点重合时停止运动;设平移的距离为,正方形的边与交于点,所在的直线与交于点,连接,是否存在这样的,使⊿是等腰三角形?若存在,求的值;若不存在,请说明理由.
35.如图,抛物线过点两点,点关于抛物线的对称轴对称,过点作直线轴,交轴于点 .
⑴.求抛物线的解析式;
⑵.直接写出点的坐标,并求出⊿的面积;
⑶.点是抛物线上的动点,且位于第四象限,当⊿的面积为6时,求出点的坐标;
⑷.若点在直线上运动,点在轴上运动,当以点为顶点的三角形为等腰直角三角形时,请直接写出此时⊿的面积.
36.已知抛物线与轴交于(点在点的左侧),点是抛物线上的一个动点,且,,如图所示:
⑴.求抛物线的解析式;
⑵.设点为抛物线上的一个动点。且在曲线上移动.
①.当点在曲线之间(含端点)移动时,是否存在点使⊿的面积为?若存在,求点的坐标;若不存在,请说明理由;
②.当点在曲线之间(含端点)移动时,求的最大值及最大值时点的坐标.
2020.5.9
赵化中学2020中考专题复习和训练:运动型问题例谈 第 27页(共 28页) 第 28页 (共 28页)
同课章节目录
