人教版八年级下册19.2 一次函数同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册19.2 一次函数同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 16:29:26 | ||
图片预览



文档简介
一次函数 同步练习
一、选择题
1、一次函数的图象不经过? (??? )
A. 第一象限?????? B.第二象限?????? C.第三象限???????? D.第四象限
2、一次函数y=-x+1的图象与x轴交点的坐标是(??? )
A.(0,2)????? B.(0,1)????? C.(2,0)??????? D.(1,0)
3、方程2x+12=0的解是直线y=2x+12(??? )
A.与y轴交点的横坐标??????????? B.与y轴交点的纵坐标
C.与x轴交点的横坐标??????????? D.与x轴交点的纵坐标
4、下列函数中,y随x的增大而减少的函数是( )
A.y=2x+8????? B.y=-2+4x???? C.y=-2x+8???? D.y=4x
5、?一位母亲记录了儿子3~9岁的身高(单位:cm),由此建立身高与年龄的模型为y=7.19x+73.93.则下列说法中正确的是(??? )
A.身高与年龄是一次函数关系
B.这个模型适合所有3~9岁的孩子
C.预测这个孩子10岁时,身高一定在145.83 cm以上
D.这个孩子在3~9岁之内,年龄每增加1岁,身高平均增加约7.19 cm
6、已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是(??? )
?
7、已知一次函数的图象经过一、三、四象限,则m,n的取值范围是( )
A、,???????????? ?B、,?
C、,?????????? ???D、,?
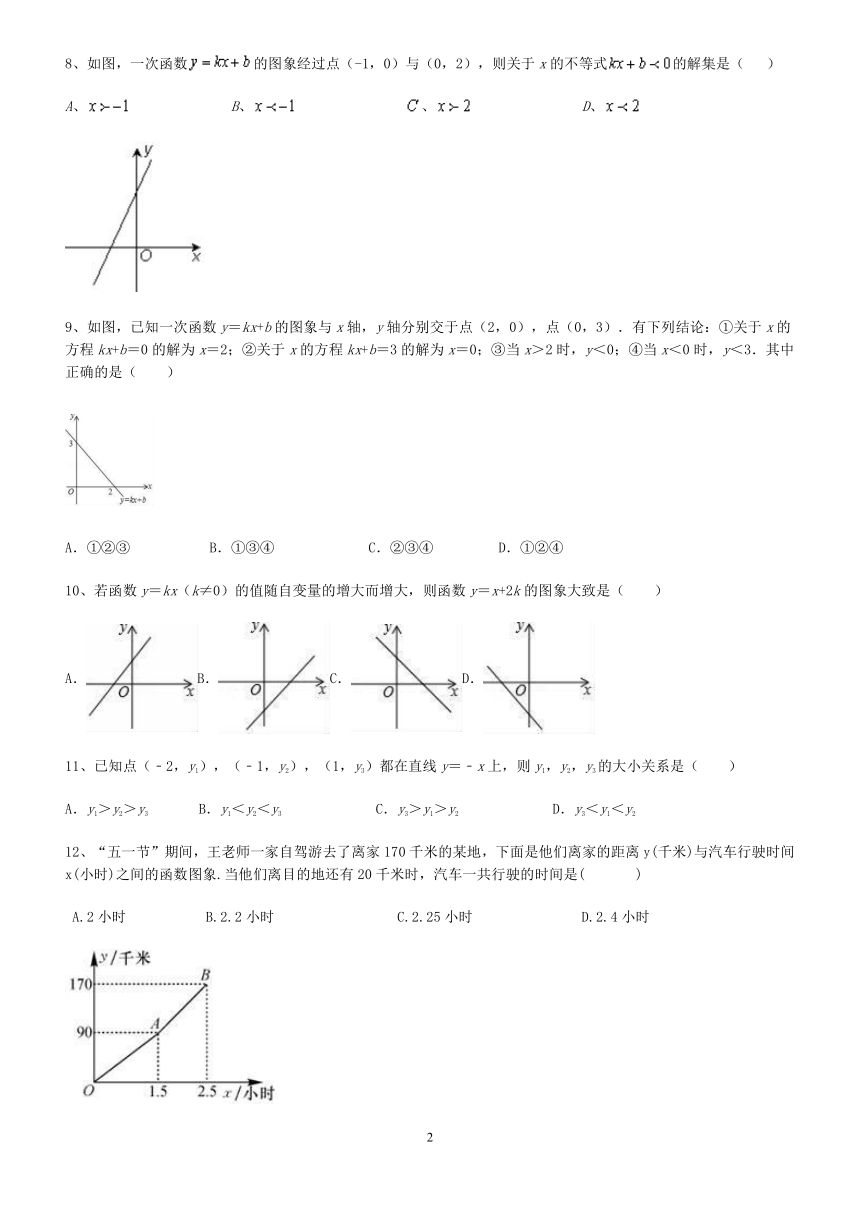
8、如图,一次函数的图象经过点(-1,0)与(0,2),则关于x的不等式的解集是( ?)
A、???????B、??????? 、??????? D、
9、如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程kx+b=0的解为x=2;②关于x的方程kx+b=3的解为x=0;③当x>2时,y<0;④当x<0时,y<3.其中正确的是( )
A.①②③????? B.①③④?????? C.②③④???? D.①②④
10、若函数y=kx(k≠0)的值随自变量的增大而增大,则函数y=x+2k的图象大致是( )
A.B.C.D.
11、已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣x上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3??? B.y1<y2<y3?????? C.y3>y1>y2?????? D.y3<y1<y2
12、“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.当他们离目的地还有20千米时,汽车一共行驶的时间是(??? )
A.2小时????? B.2.2小时???????? C.2.25小时??????? D.2.4小时
????????
二、填空题
13、若点(a,3)在函数y=2x﹣3的图象上,a的值是 ?? .
14、一次函数与轴的交点坐标是????,与轴的交点坐标是? ???,与坐标围成的三角形面积是?????.
15、若直线和直线的交点在第三象限,则的取值范围是?????.
16、已知一次函数的图象与的图象平行,而且经过点(1,1),则该一次函数的解析式为?????.
17、如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费?????元.
18、小明的爸爸用50万元购进一辆出租车(含经营权).在投入营运后,每一年营运的总收入为18.5万元,而各种费用的总支出为6万元,设该车营运x年后盈利y万元.
? (1)y与x之间的函数关系式是?????.
? (2)可预测该出租车营运?????年后开始盈利.
三、简答题
19、已知正比例函数y=kx图象经过点(3,﹣6),求:
(1)这个函数的解析式;(2)判断点A(4,﹣2)是否在这个函数图象上;
(3)图象上两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
20、已知一次函数y=kx+b的图象如图所示
(1)求k、b的值;
(2)在平面直角坐标系内画出函数y=bx+k的图象;
(3)利用(2)中你所画的图象,写出0<x<1时,y的取值范围.
21、已知y与x+2成正比,当x=4时,y=4.
(1)求y与x之间的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
22、某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图象如图所示,则此销售人员的销售量为3千件时的月收入是多少元?
23、某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期30天的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 ?? 件,日销售利润是 ?? 元.
(2)求线段DE所对应的函数关系式.(不要求写出自变量的取值范围)
(3)通过计算说明试销售期间第几天的日销售量最大?最大日销售量是多少?
参考答案
一、选择题
1、B;;2、C;3、C;4、C;;5、D;6、C;7、C;8、B;9、A;10、A;11、A;12、.C;
二、填空题
13、3
14、;
15、.
16、??;
17、7.4
18、(1)y=12.5x-50
? (2)4
三、简答题
19、解:(1)∵正比例函数y=kx经过点(3,﹣6),
∴﹣6=3?k,
解得:k=﹣2,
∴这个正比例函数的解析式为:y=﹣2x;
(2)将x=4代入y=﹣2x得:y=﹣8≠﹣2,
∴点A(4,﹣2)不在这个函数图象上;
(3)∵k=﹣2<0,
∴y随x的增大而减小,
∵x1>x2,
∴y1<y2.
20、解:(1)A(0,﹣2),B(1,0).
将A(0,﹣2),B(1,0)两点代入y=kx+b中,
得b=﹣2,k﹣2=0,k=2.
(2)对于函数y=﹣2x+2,
列表:
x 0 1
y 2 0
图象如下:
(3)由图象可得:当0<x<1时,y的取值范围为:0<y<2.
21、解:(1)设 y=k(x+2),
∵当x=4时,y=4,
∴k(4+2)=4,
∴k=,
∴y与x之间的函数关系式为y=(x+2)=x+;
(2)∵点(a,3)在这个函数图象上,
∴a+=3,
∴a=2.5.
22、设直线解析式为y=kx+b,因图象过(1,800),(2,1 100),
? ∴解得
? ∴解析式为y=300x+500,
? 当x=3时y=1 400.
? 答:此销售人员的销售量为3千件时的月收入是1 400元.
23、:(1)340﹣(24﹣22)×5=330(件),
330×(8﹣6)=660(元).
故答案为:330;660.
(2)线段DE所表示的y与x之间的函数关系式为y=340﹣5(x﹣22)=﹣5x+450;
(3)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
联立两线段所表示的函数关系式成方程组,
得,
解得:,
∴交点D的坐标为(18,360),
∵点D的坐标为(18,360),
∴试销售期间第18天的日销售量最大,最大日销售量是360件.
一、选择题
1、一次函数的图象不经过? (??? )
A. 第一象限?????? B.第二象限?????? C.第三象限???????? D.第四象限
2、一次函数y=-x+1的图象与x轴交点的坐标是(??? )
A.(0,2)????? B.(0,1)????? C.(2,0)??????? D.(1,0)
3、方程2x+12=0的解是直线y=2x+12(??? )
A.与y轴交点的横坐标??????????? B.与y轴交点的纵坐标
C.与x轴交点的横坐标??????????? D.与x轴交点的纵坐标
4、下列函数中,y随x的增大而减少的函数是( )
A.y=2x+8????? B.y=-2+4x???? C.y=-2x+8???? D.y=4x
5、?一位母亲记录了儿子3~9岁的身高(单位:cm),由此建立身高与年龄的模型为y=7.19x+73.93.则下列说法中正确的是(??? )
A.身高与年龄是一次函数关系
B.这个模型适合所有3~9岁的孩子
C.预测这个孩子10岁时,身高一定在145.83 cm以上
D.这个孩子在3~9岁之内,年龄每增加1岁,身高平均增加约7.19 cm
6、已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是(??? )
?
7、已知一次函数的图象经过一、三、四象限,则m,n的取值范围是( )
A、,???????????? ?B、,?
C、,?????????? ???D、,?
8、如图,一次函数的图象经过点(-1,0)与(0,2),则关于x的不等式的解集是( ?)
A、???????B、??????? 、??????? D、
9、如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①关于x的方程kx+b=0的解为x=2;②关于x的方程kx+b=3的解为x=0;③当x>2时,y<0;④当x<0时,y<3.其中正确的是( )
A.①②③????? B.①③④?????? C.②③④???? D.①②④
10、若函数y=kx(k≠0)的值随自变量的增大而增大,则函数y=x+2k的图象大致是( )
A.B.C.D.
11、已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣x上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3??? B.y1<y2<y3?????? C.y3>y1>y2?????? D.y3<y1<y2
12、“五一节”期间,王老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.当他们离目的地还有20千米时,汽车一共行驶的时间是(??? )
A.2小时????? B.2.2小时???????? C.2.25小时??????? D.2.4小时
????????
二、填空题
13、若点(a,3)在函数y=2x﹣3的图象上,a的值是 ?? .
14、一次函数与轴的交点坐标是????,与轴的交点坐标是? ???,与坐标围成的三角形面积是?????.
15、若直线和直线的交点在第三象限,则的取值范围是?????.
16、已知一次函数的图象与的图象平行,而且经过点(1,1),则该一次函数的解析式为?????.
17、如图所示中的折线ABC为甲地向乙地打长途电话需付的电话费y(元)与通话时间t(分钟)之间的函数关系,则通话8分钟应付电话费?????元.
18、小明的爸爸用50万元购进一辆出租车(含经营权).在投入营运后,每一年营运的总收入为18.5万元,而各种费用的总支出为6万元,设该车营运x年后盈利y万元.
? (1)y与x之间的函数关系式是?????.
? (2)可预测该出租车营运?????年后开始盈利.
三、简答题
19、已知正比例函数y=kx图象经过点(3,﹣6),求:
(1)这个函数的解析式;(2)判断点A(4,﹣2)是否在这个函数图象上;
(3)图象上两点B(x1,y1)、C(x2,y2),如果x1>x2,比较y1,y2的大小.
20、已知一次函数y=kx+b的图象如图所示
(1)求k、b的值;
(2)在平面直角坐标系内画出函数y=bx+k的图象;
(3)利用(2)中你所画的图象,写出0<x<1时,y的取值范围.
21、已知y与x+2成正比,当x=4时,y=4.
(1)求y与x之间的函数关系式;
(2)若点(a,3)在这个函数图象上,求a的值.
22、某公司销售人员的个人月收入与其每月的销售量成一次函数关系,图象如图所示,则此销售人员的销售量为3千件时的月收入是多少元?
23、某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期30天的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成如图所示的图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 ?? 件,日销售利润是 ?? 元.
(2)求线段DE所对应的函数关系式.(不要求写出自变量的取值范围)
(3)通过计算说明试销售期间第几天的日销售量最大?最大日销售量是多少?
参考答案
一、选择题
1、B;;2、C;3、C;4、C;;5、D;6、C;7、C;8、B;9、A;10、A;11、A;12、.C;
二、填空题
13、3
14、;
15、.
16、??;
17、7.4
18、(1)y=12.5x-50
? (2)4
三、简答题
19、解:(1)∵正比例函数y=kx经过点(3,﹣6),
∴﹣6=3?k,
解得:k=﹣2,
∴这个正比例函数的解析式为:y=﹣2x;
(2)将x=4代入y=﹣2x得:y=﹣8≠﹣2,
∴点A(4,﹣2)不在这个函数图象上;
(3)∵k=﹣2<0,
∴y随x的增大而减小,
∵x1>x2,
∴y1<y2.
20、解:(1)A(0,﹣2),B(1,0).
将A(0,﹣2),B(1,0)两点代入y=kx+b中,
得b=﹣2,k﹣2=0,k=2.
(2)对于函数y=﹣2x+2,
列表:
x 0 1
y 2 0
图象如下:
(3)由图象可得:当0<x<1时,y的取值范围为:0<y<2.
21、解:(1)设 y=k(x+2),
∵当x=4时,y=4,
∴k(4+2)=4,
∴k=,
∴y与x之间的函数关系式为y=(x+2)=x+;
(2)∵点(a,3)在这个函数图象上,
∴a+=3,
∴a=2.5.
22、设直线解析式为y=kx+b,因图象过(1,800),(2,1 100),
? ∴解得
? ∴解析式为y=300x+500,
? 当x=3时y=1 400.
? 答:此销售人员的销售量为3千件时的月收入是1 400元.
23、:(1)340﹣(24﹣22)×5=330(件),
330×(8﹣6)=660(元).
故答案为:330;660.
(2)线段DE所表示的y与x之间的函数关系式为y=340﹣5(x﹣22)=﹣5x+450;
(3)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
联立两线段所表示的函数关系式成方程组,
得,
解得:,
∴交点D的坐标为(18,360),
∵点D的坐标为(18,360),
∴试销售期间第18天的日销售量最大,最大日销售量是360件.
