人教版八年级下册数学19.1.2函数的图像(1)教案
文档属性
| 名称 | 人教版八年级下册数学19.1.2函数的图像(1)教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 118.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 22:43:24 | ||
图片预览

文档简介
19.1.2函数的图像------第一课时:.函数的图像(1)----画图,识图
学习目标
了解函数图像的意义,能在平面直角坐标系中画出简单的函数图像
动手实验,通过列表,描点,连线,掌握基本的画图能力
教学重难点
重点:函数图像的画法,观察分析图像的信息
难点:函数图像的理解,概括图像中的信息
教学过程
一.情镜引入
对于很难用式子表示的函数关系,我们可以用图来直观地反映.即使能用式子表示的函数关系,也可以画图表示,则会使函数关系更清晰.比如用心电图表示心脏部位的生物电流与时间的关系.(同时展示本节课的学习目标)
二.新知探究,合作交流(自学研讨后以小组学习的方式进行)
探究一:函数的图像
函数的图像
阅读教材P75---P77内容,回答什么是函数的图像?并让学生练习识图.
学生小组讨论之后回答,如果出现问题让另一个小组补充回答:对于一个函数,
如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点 组成的图形,就是这个函数的图象.
让学生自己体会理解函数图像所提供的信息;
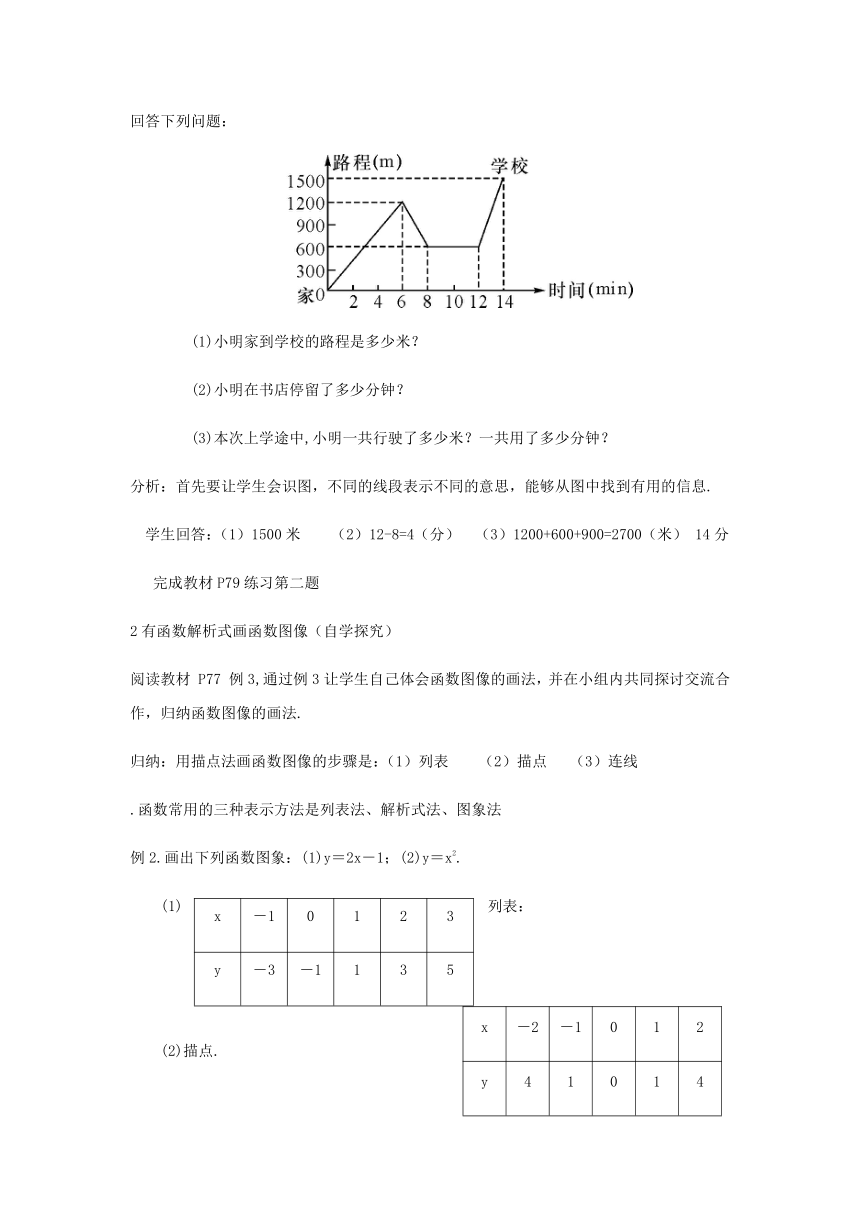
例1.小东骑自行车去上学,当他骑了一段时,想起要买字典,于是又折回到刚经过的书店,买到字典后继续去学校,如图是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
分析:首先要让学生会识图,不同的线段表示不同的意思,能够从图中找到有用的信息.
学生回答:(1)1500米 (2)12-8=4(分) (3)1200+600+900=2700(米) 14分
完成教材P79练习第二题
2有函数解析式画函数图像(自学探究)
阅读教材 P77 例3,通过例3让学生自己体会函数图像的画法,并在小组内共同探讨交流合作,归纳函数图像的画法.
归纳:用描点法画函数图像的步骤是:(1)列表 (2)描点 (3)连线
.函数常用的三种表示方法是列表法、解析式法、图象法
例2.画出下列函数图象:(1)y=2x-1;(2)y=x2.
x -1 0 1 2 3
y -3 -1 1 3 5
x -2 -1 0 1 2
y 4 1 0 1 4
(1)列表:
(2)描点.
(3)连线.
三,巩固练习
1 .近一个月来漳州市遭受暴雨袭击,九龙江水位上涨.
小明以警戒水位为原点,用折线统计图表示某一天江水水位情况.请你结合折线统计图判断下列叙述不正确的是( ) .
A.8时水位最高 B.这一天水位均高于警戒水位
C.8时到16时水位都在下降 D.P 点表示12时水位高于警戒水位0.6米
2. 已知点(2,5)在函数y=ax-3的图象上,则a的值为( )
A.4 B.-4 C.10 D.-10
3.画出下列函数图象:(1)y=2x+1;(2)y=x2.(x>0)
四.总结拓展
1.课堂小结:学生讨论交流回答下面的四个问题
(1)用描点法画函数图像的步骤是:(1)列表 (2)描点 (3)连线
(2)从函数图像上获取提供的信息
2.拓展延伸
1.如图是某一函数的图象,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y值最大?当x取何值时y值最小?
(5)当x的值在什么范围内时y随x的增大而增大?当x的值在什么范围内时y随x的增大而减小?
3.作业布置:教材P92---P83,习题第7,8,9题
五.课堂效果测评
1、海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐与人类的生活有着密切的联系.下面是某港口从0时到12时的水深情况:
(1)大约什么时刻港口水最深?深度约是多少?
(2)大约什么时刻港口水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
(4)在什么时间范围内,港口水深在减少?
(5)A、B两点分别表示什么?还有几时水的深度与A点所表示的深度相同?
(6)说一说这个港口从0时到12时的水深是怎样变化的?
2.下列各点中在函数y=3x-1的图象上的是( )
(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
3.如图所示的图象分别给出了x与y的对应关系,其中y是x的函数的是( )
4.画出函数的图象
x … …
y … …
六.评价与反思(引导学生自己总结)
1.你今天学习了什么?学到了什么?还有什么疑惑?有什么感受?在学生回答的基础上,教师点评并板书
2.教学反思
本节课让学生自己动手一步一步的按照列表,描点,连线的步骤画出函数的图象,并在老师的详细讲解下理解了图象的概念,这种通过学生自己动手来接受新知识的方法以后还要加强.
学习目标
了解函数图像的意义,能在平面直角坐标系中画出简单的函数图像
动手实验,通过列表,描点,连线,掌握基本的画图能力
教学重难点
重点:函数图像的画法,观察分析图像的信息
难点:函数图像的理解,概括图像中的信息
教学过程
一.情镜引入
对于很难用式子表示的函数关系,我们可以用图来直观地反映.即使能用式子表示的函数关系,也可以画图表示,则会使函数关系更清晰.比如用心电图表示心脏部位的生物电流与时间的关系.(同时展示本节课的学习目标)
二.新知探究,合作交流(自学研讨后以小组学习的方式进行)
探究一:函数的图像
函数的图像
阅读教材P75---P77内容,回答什么是函数的图像?并让学生练习识图.
学生小组讨论之后回答,如果出现问题让另一个小组补充回答:对于一个函数,
如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点 组成的图形,就是这个函数的图象.
让学生自己体会理解函数图像所提供的信息;
例1.小东骑自行车去上学,当他骑了一段时,想起要买字典,于是又折回到刚经过的书店,买到字典后继续去学校,如图是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
分析:首先要让学生会识图,不同的线段表示不同的意思,能够从图中找到有用的信息.
学生回答:(1)1500米 (2)12-8=4(分) (3)1200+600+900=2700(米) 14分
完成教材P79练习第二题
2有函数解析式画函数图像(自学探究)
阅读教材 P77 例3,通过例3让学生自己体会函数图像的画法,并在小组内共同探讨交流合作,归纳函数图像的画法.
归纳:用描点法画函数图像的步骤是:(1)列表 (2)描点 (3)连线
.函数常用的三种表示方法是列表法、解析式法、图象法
例2.画出下列函数图象:(1)y=2x-1;(2)y=x2.
x -1 0 1 2 3
y -3 -1 1 3 5
x -2 -1 0 1 2
y 4 1 0 1 4
(1)列表:
(2)描点.
(3)连线.
三,巩固练习
1 .近一个月来漳州市遭受暴雨袭击,九龙江水位上涨.
小明以警戒水位为原点,用折线统计图表示某一天江水水位情况.请你结合折线统计图判断下列叙述不正确的是( ) .
A.8时水位最高 B.这一天水位均高于警戒水位
C.8时到16时水位都在下降 D.P 点表示12时水位高于警戒水位0.6米
2. 已知点(2,5)在函数y=ax-3的图象上,则a的值为( )
A.4 B.-4 C.10 D.-10
3.画出下列函数图象:(1)y=2x+1;(2)y=x2.(x>0)
四.总结拓展
1.课堂小结:学生讨论交流回答下面的四个问题
(1)用描点法画函数图像的步骤是:(1)列表 (2)描点 (3)连线
(2)从函数图像上获取提供的信息
2.拓展延伸
1.如图是某一函数的图象,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y值最大?当x取何值时y值最小?
(5)当x的值在什么范围内时y随x的增大而增大?当x的值在什么范围内时y随x的增大而减小?
3.作业布置:教材P92---P83,习题第7,8,9题
五.课堂效果测评
1、海水受日月的引力而产生潮汐现象,早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐与人类的生活有着密切的联系.下面是某港口从0时到12时的水深情况:
(1)大约什么时刻港口水最深?深度约是多少?
(2)大约什么时刻港口水最浅?深度约是多少?
(3)在什么时间范围内,港口水深在增加?
(4)在什么时间范围内,港口水深在减少?
(5)A、B两点分别表示什么?还有几时水的深度与A点所表示的深度相同?
(6)说一说这个港口从0时到12时的水深是怎样变化的?
2.下列各点中在函数y=3x-1的图象上的是( )
(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
3.如图所示的图象分别给出了x与y的对应关系,其中y是x的函数的是( )
4.画出函数的图象
x … …
y … …
六.评价与反思(引导学生自己总结)
1.你今天学习了什么?学到了什么?还有什么疑惑?有什么感受?在学生回答的基础上,教师点评并板书
2.教学反思
本节课让学生自己动手一步一步的按照列表,描点,连线的步骤画出函数的图象,并在老师的详细讲解下理解了图象的概念,这种通过学生自己动手来接受新知识的方法以后还要加强.
