北师大版九年级下册数学3.4圆心角与圆周角的关系教案
文档属性
| 名称 | 北师大版九年级下册数学3.4圆心角与圆周角的关系教案 |  | |
| 格式 | zip | ||
| 文件大小 | 672.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 22:50:28 | ||
图片预览

文档简介
圆周角与圆心角的关系
一、学生知识状况分析
学生的知识技能基础:学生在上一节的内容中已掌握了圆心角的定义及圆心角的性质。掌握了在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。初步了解研究图形的方法,如折叠、轴对称、旋转、证明等。
学生的活动经验基础:在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
二、教学目标:
1. 了解圆周角的概念。
2.理解圆周角定理的证明。
3经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想。
三教学重难点:
教学重点:圆周角概念及圆周角定理。
教学难点:认识圆周角定理需分三种情况证明的必要性。
三、教学过程分析
第一环节 创设问题情境,引入新课
出示问题:在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。如图,当他站在B,D,E的位置射球时对球门AC的张角的大小是相等的?为什么呢?你能观察到这三个角有什么共同特征吗?
活动目的:
通过此问题引起学生学习的兴趣。此问题意在通过射门游戏引入圆周角的概念。同时为第2课时的学习埋下伏笔.
第二环节 讲授新课
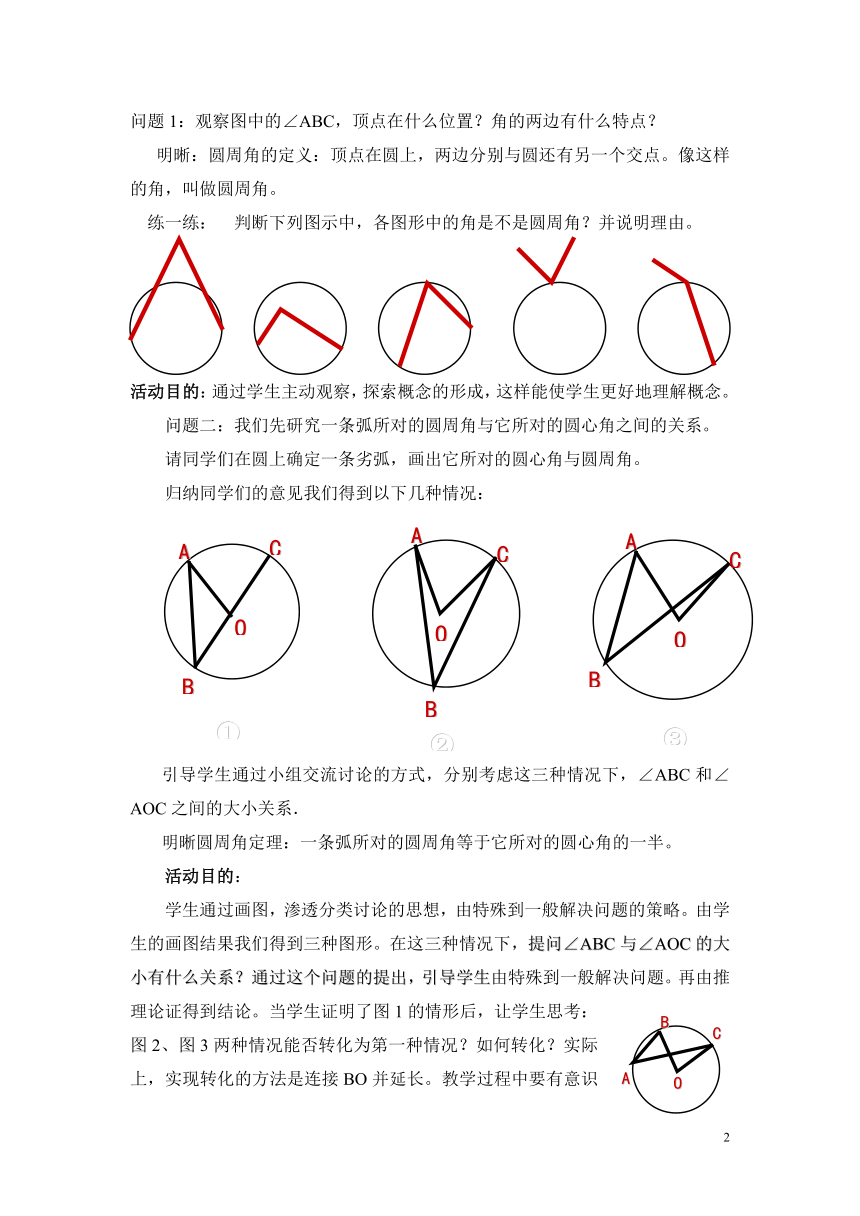
问题1:观察图中的∠ABC,顶点在什么位置?角的两边有什么特点?
明晰:圆周角的定义:顶点在圆上,两边分别与圆还有另一个交点。像这样的角,叫做圆周角。
练一练: 判断下列图示中,各图形中的角是不是圆周角?并说明理由。
活动目的:通过学生主动观察,探索概念的形成,这样能使学生更好地理解概念。
问题二:我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
归纳同学们的意见我们得到以下几种情况:
引导学生通过小组交流讨论的方式,分别考虑这三种情况下,∠ABC和∠AOC之间的大小关系.
明晰圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
活动目的:
学生通过画图,渗透分类讨论的思想,由特殊到一般解决问题的策略。由学生的画图结果我们得到三种图形。在这三种情况下,提问∠ABC与∠AOC的大小有什么关系?通过这个问题的提出,引导学生由特殊到一般解决问题。再由推理论证得到结论。当学生证明了图1的情形后,让学生思考:图2、图3两种情况能否转化为第一种情况?如何转化?实际上,实现转化的方法是连接BO并延长。教学过程中要有意识地向学生渗透解决问题的策略以及转化、分类、归纳等数学思想方法。
第三环节 练一练
1.如图,在⊙O中,∠BOC=50°,则∠BAC= 。
变化题1:如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠BOC=
变化题2:如图,∠BAC=40°,则∠OBC=
2.如图,OA,OB,OC都是⊙O的半径,∠ AOB=2∠ BOC,∠ ACB与∠ BAC的大小有什么关系?为什么?
第2题图 第3题图
3.如图,A,B,C,D是⊙O上的四点,且∠BCD=100° ,求∠BOD(BCD所对的圆心角)和∠BAD的大小。
4. 如图,当他站在B,D,E的位置射球时
对球门AC的张角的大小是相等的?为什么呢?
活动目的:
通过练习目的是使学生熟练地掌握圆周角与圆心角的关系。通过图形和条件的变化,让学生了解要找出圆周角与圆心角的关系,就必须找出它们所对的同一条弧。
第四环节 课堂小结
到目前为止,我们学习到和圆有关的角有几个?它们各有什么特点?相互之间有什么关系?
第五环节 布置作业
四、教学反思
把射门游戏问题抽象为数学问题,研究圆周角和圆心角的关系,研究圆周角和圆心角的关系,应该说,学生解决这一问题是有一定难度的,尽管如此,教学时仍应给学生留有时间和空间,让他们进行思考。让学生经历观察、想象、推理、操作、描述、交流等过程,多种角度直观体验数学模型,而这也正符合本章学习的主要目标。
B
A
O
C
①
A
B
C
O
②
B
A
C
O
③
A
O
C
B
A
B
C
O
A
B
C
O
A
B
C
D
O
PAGE
1
一、学生知识状况分析
学生的知识技能基础:学生在上一节的内容中已掌握了圆心角的定义及圆心角的性质。掌握了在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。初步了解研究图形的方法,如折叠、轴对称、旋转、证明等。
学生的活动经验基础:在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
二、教学目标:
1. 了解圆周角的概念。
2.理解圆周角定理的证明。
3经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想。
三教学重难点:
教学重点:圆周角概念及圆周角定理。
教学难点:认识圆周角定理需分三种情况证明的必要性。
三、教学过程分析
第一环节 创设问题情境,引入新课
出示问题:在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。如图,当他站在B,D,E的位置射球时对球门AC的张角的大小是相等的?为什么呢?你能观察到这三个角有什么共同特征吗?
活动目的:
通过此问题引起学生学习的兴趣。此问题意在通过射门游戏引入圆周角的概念。同时为第2课时的学习埋下伏笔.
第二环节 讲授新课
问题1:观察图中的∠ABC,顶点在什么位置?角的两边有什么特点?
明晰:圆周角的定义:顶点在圆上,两边分别与圆还有另一个交点。像这样的角,叫做圆周角。
练一练: 判断下列图示中,各图形中的角是不是圆周角?并说明理由。
活动目的:通过学生主动观察,探索概念的形成,这样能使学生更好地理解概念。
问题二:我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
归纳同学们的意见我们得到以下几种情况:
引导学生通过小组交流讨论的方式,分别考虑这三种情况下,∠ABC和∠AOC之间的大小关系.
明晰圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
活动目的:
学生通过画图,渗透分类讨论的思想,由特殊到一般解决问题的策略。由学生的画图结果我们得到三种图形。在这三种情况下,提问∠ABC与∠AOC的大小有什么关系?通过这个问题的提出,引导学生由特殊到一般解决问题。再由推理论证得到结论。当学生证明了图1的情形后,让学生思考:图2、图3两种情况能否转化为第一种情况?如何转化?实际上,实现转化的方法是连接BO并延长。教学过程中要有意识地向学生渗透解决问题的策略以及转化、分类、归纳等数学思想方法。
第三环节 练一练
1.如图,在⊙O中,∠BOC=50°,则∠BAC= 。
变化题1:如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠BOC=
变化题2:如图,∠BAC=40°,则∠OBC=
2.如图,OA,OB,OC都是⊙O的半径,∠ AOB=2∠ BOC,∠ ACB与∠ BAC的大小有什么关系?为什么?
第2题图 第3题图
3.如图,A,B,C,D是⊙O上的四点,且∠BCD=100° ,求∠BOD(BCD所对的圆心角)和∠BAD的大小。
4. 如图,当他站在B,D,E的位置射球时
对球门AC的张角的大小是相等的?为什么呢?
活动目的:
通过练习目的是使学生熟练地掌握圆周角与圆心角的关系。通过图形和条件的变化,让学生了解要找出圆周角与圆心角的关系,就必须找出它们所对的同一条弧。
第四环节 课堂小结
到目前为止,我们学习到和圆有关的角有几个?它们各有什么特点?相互之间有什么关系?
第五环节 布置作业
四、教学反思
把射门游戏问题抽象为数学问题,研究圆周角和圆心角的关系,研究圆周角和圆心角的关系,应该说,学生解决这一问题是有一定难度的,尽管如此,教学时仍应给学生留有时间和空间,让他们进行思考。让学生经历观察、想象、推理、操作、描述、交流等过程,多种角度直观体验数学模型,而这也正符合本章学习的主要目标。
B
A
O
C
①
A
B
C
O
②
B
A
C
O
③
A
O
C
B
A
B
C
O
A
B
C
O
A
B
C
D
O
PAGE
1
