人教版数学七年级下册 9.3 一元一次不等式组同步练习(含答案)
文档属性
| 名称 | 人教版数学七年级下册 9.3 一元一次不等式组同步练习(含答案) | 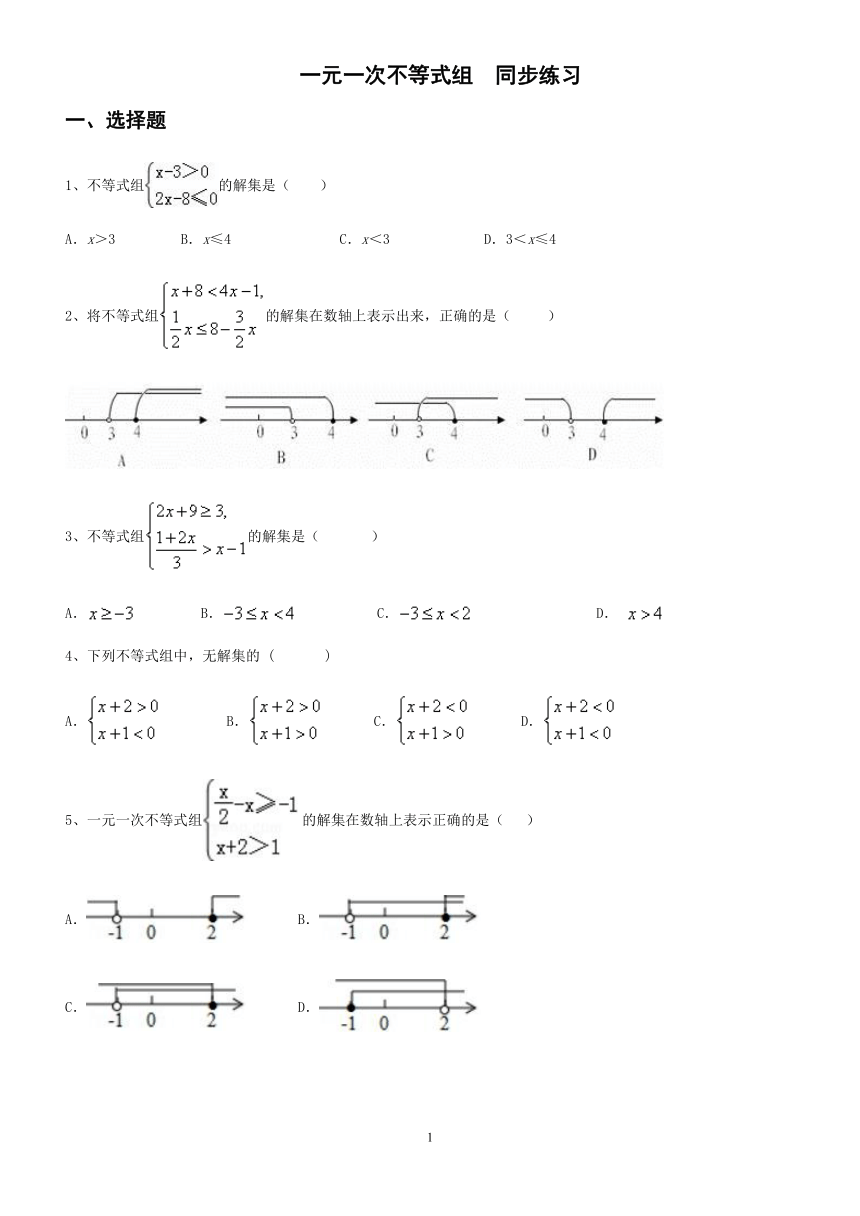 | |
| 格式 | zip | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 17:47:39 | ||
图片预览
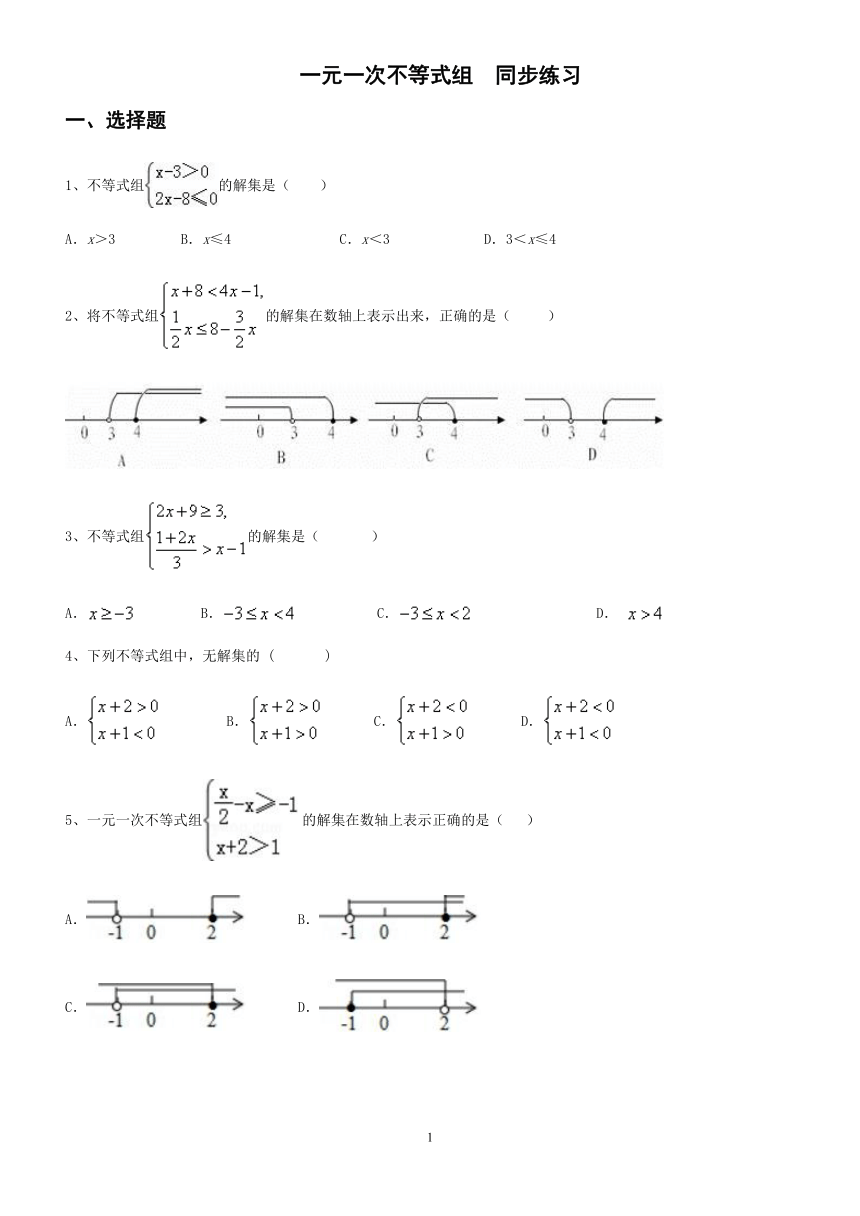



文档简介
一元一次不等式组 同步练习
一、选择题
1、不等式组的解集是( )
A.x>3???? B.x≤4??????? C.x<3?????? D.3<x≤4
2、将不等式组的解集在数轴上表示出来,正确的是( ? )
3、不等式组的解集是(??? )
A.???? B.????? C.???????? D.
4、下列不等式组中,无解集的 (??? )
A. ??? B.??? C.??? D.
5、一元一次不等式组的解集在数轴上表示正确的是(? )
A.??? B.???
C.??? D.
6、如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A.? B.? C.? D.
7、若关于x的一元一次不等式组的解集是x<5,则m的取值范围是( )
A.m≥5????? B.m>5????????? C.m≤5???????? D.m<5
8、不等式组的正整数解的个数是( )
A.5????B.4????????? C.3?????? D.2??
9、已知方程组的解x、y满足2x+y≥0,则m的取值范围是(?? ??)
A.m≥-? B.m≥? C.m≥1?? ? D.-≤m≤1
10、某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人,如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒,则这个敬老院的老人最少有(??? )
A.29人?????? B.30人?????? C.31人????? D.32人
11、四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S,如下图所示,则他们的体重大小关系是(?? )
A.P>R>S>Q??? ?? B.Q>S>P>R?????? C.S>P>Q>R???????? D.S>P>R>Q
12、如果将长度为、和的三根线段首尾顺次相接可以得到一个三角形,那么的取值范围是??? (??? )
A.??? B.?? ???? C.??? ????? D.无法确定
2、填空题
13、满足不等式组的整数x为__________.
14、若不等式组无解,则的取值范围是?????.
15、若不等式组的解集是>3,则的取值范围是?????.
16、从小明家到学校的路程是2 400米,如果小明早上7点离家,要在7点30分到40分之间到达学校,设步行速度为米/分,则可列不等式组为??????????,小明步行的速度范围是?????.
17、小芳上午10时开始以每小时4km的速度从甲地赶往乙地,到达时已超过下午1时,但不到1时45分,则甲、乙两地距离的范围是?????.
18、规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简[x]+(x)+[x)的结果是 ?? .
三、简答题
19、已知,x满足化简:.
20、国庆节期间,电器市场火爆.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别 电视机 洗衣机
进价(元/台) 1 800 1 500
售价(元/台) 2 000 1 600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
21、?2011年我市筹备30周年庆典,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
22、日照市是中国北方最大的对虾养殖产区,被国家农业部列为对虾养殖重点区域;贝类产品西施舌是日照特产.沿海某养殖场计划今年养殖无公害标准化对虾和西施舌,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表: (单位:千元/吨)
品种 先期投资 养殖期间投资 产值
西施舌 9 3 30
对虾 4 10 20
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.
设西施舌种苗的投放量为x吨
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,
并求出当x等于多少时,y有最大值?最大值是多少?
23、某校师生积极为汶川地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格每顶160元,供10人居住的大帐篷,价格每顶400元,学校花去捐款96000元,采购这两种帐篷,正好可供2300人临时居住。
(1)求该校采购了多少顶3人小帐篷,多少顶10人大帐篷;
(2)学校现计划租用甲、乙两种型号的卡车共20辆,将这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运9顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷,如何安排甲、乙两种卡车可一次将这批帐篷运往灾区?有哪几种方案?
参考答案
一、选择题
1、D;2、C;3、B;4、C;5、C.;6、C.;7、A;8、C.;9、A;10、B;11、D;12、C;
二、填空题
13、-2,-1,0,1?
14、
15、m3?
16、? 60米/分~80米/分?
17、(12~15)km.
18、﹣2或﹣1或0或1或2.
三、简答题
19、7;
20、解:(1)设商店购进电视机x台,则购进洗衣机(100-x)台,根据题意,得
解不等式组,得 ≤x≤.即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得y=(2 000-1 800)x+(1 600-1 500)(100-x)=100x+10 000. 因为100>0,所以当x最大时,y的值最大.即当x=39时,商店获利最多为13 900元.
21、解:设搭配种造型个,则种造型为个,依题意,得:
?,解这个不等式组,得:,?
是整数,可取,可设计三种搭配方案:
①种园艺造型个 种园艺造型个
②种园艺造型个 种园艺造型个
③种园艺造型个 种园艺造型个.
(2)方法一:由于种造型的造价成本高于种造型成本.所以种造型越少,成本越低,故应选择方案③,成本最低,最低成本为:(元)
方法二:方案①需成本:(元)
方案②需成本:(元)
方案③需成本:元
应选择方案③,成本最低,最低成本为元?
22、解:(1)设西施舌的投放量为x吨,则对虾的投放量为(50-x)吨,
根据题意,得:??????
????? 解之,得:????
?????????? ∴30≤x≤32;
(2)y=30x+20(50-x)=10x+1000.?????
∵30≤x≤32,100>0,∴1300≤x≤1320,
?∴ y的最大值是1320,
?? ?因此当x=32时,y有最大值,且最大值是1320千元.?
23、解:( 1)设该校采购了x 顶小帐篷,y 顶大帐遥.
根据题意,得
解这个方程组.得
?( 2 )设甲型卡车安排了辆。则乙型卡车安排了( 20 -)辆.
根据题意,得
解这个不等式组.得
∵车辆数为正整数,∴ 或16 或17
?∴
答:( 1 )该校采购了100 顶小帐篷.200 顶大帐篷.
??? ( 2 )安排方案有:① 甲型卡车15 辆,乙型卡车5 辆:② 甲型卡车16 辆,乙型卡车4 辆:③甲型卡车17辆,乙型卡车3辆.
一、选择题
1、不等式组的解集是( )
A.x>3???? B.x≤4??????? C.x<3?????? D.3<x≤4
2、将不等式组的解集在数轴上表示出来,正确的是( ? )
3、不等式组的解集是(??? )
A.???? B.????? C.???????? D.
4、下列不等式组中,无解集的 (??? )
A. ??? B.??? C.??? D.
5、一元一次不等式组的解集在数轴上表示正确的是(? )
A.??? B.???
C.??? D.
6、如果点P(2x+6,x﹣4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
A.? B.? C.? D.
7、若关于x的一元一次不等式组的解集是x<5,则m的取值范围是( )
A.m≥5????? B.m>5????????? C.m≤5???????? D.m<5
8、不等式组的正整数解的个数是( )
A.5????B.4????????? C.3?????? D.2??
9、已知方程组的解x、y满足2x+y≥0,则m的取值范围是(?? ??)
A.m≥-? B.m≥? C.m≥1?? ? D.-≤m≤1
10、某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人,如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒,则这个敬老院的老人最少有(??? )
A.29人?????? B.30人?????? C.31人????? D.32人
11、四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S,如下图所示,则他们的体重大小关系是(?? )
A.P>R>S>Q??? ?? B.Q>S>P>R?????? C.S>P>Q>R???????? D.S>P>R>Q
12、如果将长度为、和的三根线段首尾顺次相接可以得到一个三角形,那么的取值范围是??? (??? )
A.??? B.?? ???? C.??? ????? D.无法确定
2、填空题
13、满足不等式组的整数x为__________.
14、若不等式组无解,则的取值范围是?????.
15、若不等式组的解集是>3,则的取值范围是?????.
16、从小明家到学校的路程是2 400米,如果小明早上7点离家,要在7点30分到40分之间到达学校,设步行速度为米/分,则可列不等式组为??????????,小明步行的速度范围是?????.
17、小芳上午10时开始以每小时4km的速度从甲地赶往乙地,到达时已超过下午1时,但不到1时45分,则甲、乙两地距离的范围是?????.
18、规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.当﹣1<x<1时,化简[x]+(x)+[x)的结果是 ?? .
三、简答题
19、已知,x满足化简:.
20、国庆节期间,电器市场火爆.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别 电视机 洗衣机
进价(元/台) 1 800 1 500
售价(元/台) 2 000 1 600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
21、?2011年我市筹备30周年庆典,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个种造型需甲种花卉80盆,乙种花卉40盆,搭配一个种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个种造型的成本是800元,搭配一个种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
22、日照市是中国北方最大的对虾养殖产区,被国家农业部列为对虾养殖重点区域;贝类产品西施舌是日照特产.沿海某养殖场计划今年养殖无公害标准化对虾和西施舌,由于受养殖水面的制约,这两个品种的苗种的总投放量只有50吨.根据经验测算,这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表: (单位:千元/吨)
品种 先期投资 养殖期间投资 产值
西施舌 9 3 30
对虾 4 10 20
养殖场受经济条件的影响,先期投资不超过360千元,养殖期间的投资不超过290千元.
设西施舌种苗的投放量为x吨
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(千元),试写出y与x之间的函数关系式,
并求出当x等于多少时,y有最大值?最大值是多少?
23、某校师生积极为汶川地震灾区捐款,在得知灾区急需帐篷后,立即到当地的一家帐篷厂采购,帐篷有两种规格:可供3人居住的小帐篷,价格每顶160元,供10人居住的大帐篷,价格每顶400元,学校花去捐款96000元,采购这两种帐篷,正好可供2300人临时居住。
(1)求该校采购了多少顶3人小帐篷,多少顶10人大帐篷;
(2)学校现计划租用甲、乙两种型号的卡车共20辆,将这批帐篷紧急运往灾区,已知甲型卡车每辆可同时装运9顶小帐篷和11顶大帐篷,乙型卡车每辆可同时装运12顶小帐篷和7顶大帐篷,如何安排甲、乙两种卡车可一次将这批帐篷运往灾区?有哪几种方案?
参考答案
一、选择题
1、D;2、C;3、B;4、C;5、C.;6、C.;7、A;8、C.;9、A;10、B;11、D;12、C;
二、填空题
13、-2,-1,0,1?
14、
15、m3?
16、? 60米/分~80米/分?
17、(12~15)km.
18、﹣2或﹣1或0或1或2.
三、简答题
19、7;
20、解:(1)设商店购进电视机x台,则购进洗衣机(100-x)台,根据题意,得
解不等式组,得 ≤x≤.即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得y=(2 000-1 800)x+(1 600-1 500)(100-x)=100x+10 000. 因为100>0,所以当x最大时,y的值最大.即当x=39时,商店获利最多为13 900元.
21、解:设搭配种造型个,则种造型为个,依题意,得:
?,解这个不等式组,得:,?
是整数,可取,可设计三种搭配方案:
①种园艺造型个 种园艺造型个
②种园艺造型个 种园艺造型个
③种园艺造型个 种园艺造型个.
(2)方法一:由于种造型的造价成本高于种造型成本.所以种造型越少,成本越低,故应选择方案③,成本最低,最低成本为:(元)
方法二:方案①需成本:(元)
方案②需成本:(元)
方案③需成本:元
应选择方案③,成本最低,最低成本为元?
22、解:(1)设西施舌的投放量为x吨,则对虾的投放量为(50-x)吨,
根据题意,得:??????
????? 解之,得:????
?????????? ∴30≤x≤32;
(2)y=30x+20(50-x)=10x+1000.?????
∵30≤x≤32,100>0,∴1300≤x≤1320,
?∴ y的最大值是1320,
?? ?因此当x=32时,y有最大值,且最大值是1320千元.?
23、解:( 1)设该校采购了x 顶小帐篷,y 顶大帐遥.
根据题意,得
解这个方程组.得
?( 2 )设甲型卡车安排了辆。则乙型卡车安排了( 20 -)辆.
根据题意,得
解这个不等式组.得
∵车辆数为正整数,∴ 或16 或17
?∴
答:( 1 )该校采购了100 顶小帐篷.200 顶大帐篷.
??? ( 2 )安排方案有:① 甲型卡车15 辆,乙型卡车5 辆:② 甲型卡车16 辆,乙型卡车4 辆:③甲型卡车17辆,乙型卡车3辆.
