北师大版九年级数学下册3.2 圆的对称性同步测试含答案
文档属性
| 名称 | 北师大版九年级数学下册3.2 圆的对称性同步测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 08:25:15 | ||
图片预览

文档简介
3.2 圆的对称性
同步测试
1、选择题
1.下列说法中,正确的是( )
A.等弦所对的弧相等 B.等弧所对的弦相等
C.圆心角相等,所对的弦相等 D.弦相等所对的圆心角相等
2.如图,在⊙O中,∠ABC=60°,则∠AOC等于(? )
A.30°?????B.60°?????C.100°????D.120°
3.下列命题中,正确的有( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
4.下列三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等圆心角所对的弧相等。其中是真命题的是(????)
A.?①②????B.?②③????C.?①③????D.?①②③
5.如图,AB为⊙O的直径,C、D是⊙O上的两点,,,则∠DAC的度数是( )
A. 70° B. 45° C. 35° D. 30°
6.如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
A.20°?????B.30°?????C.40°?????D.70°
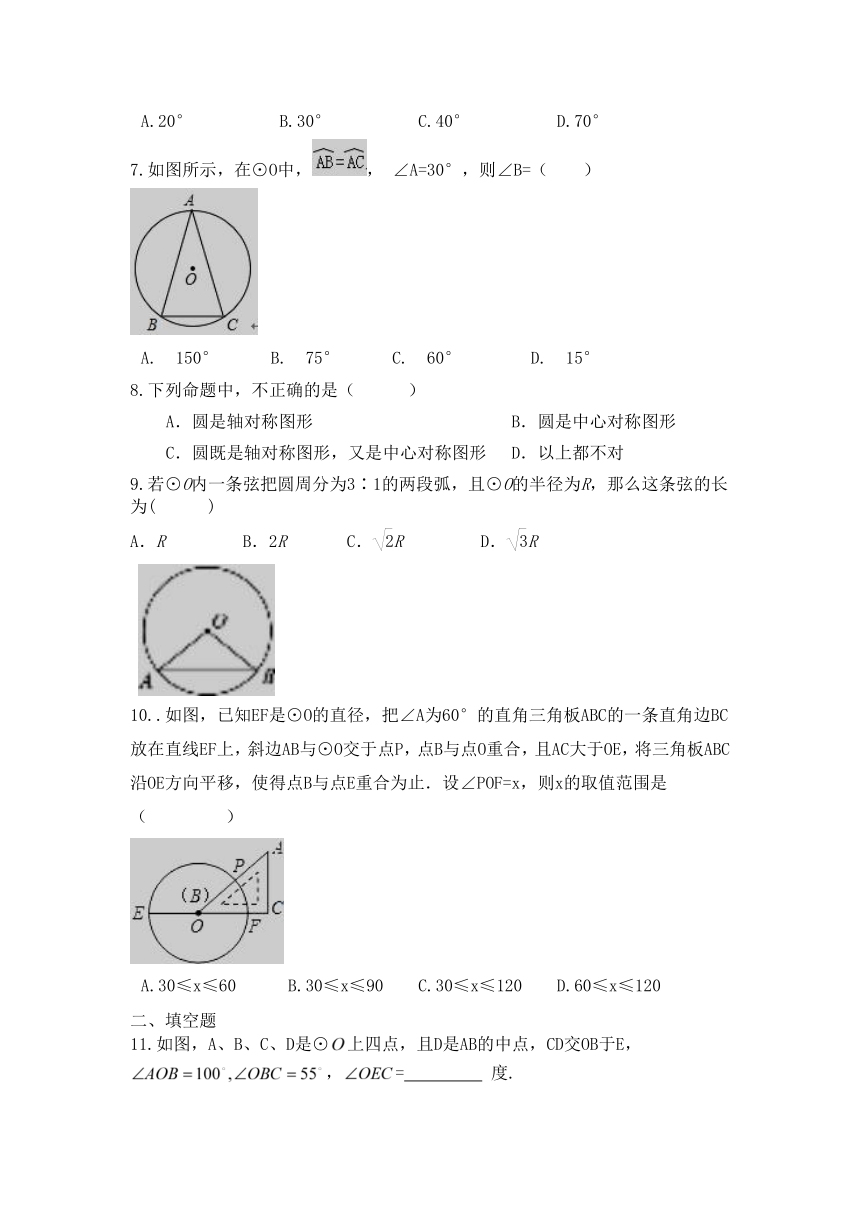
7.如图所示,在⊙O中,, ∠A=30°,则∠B=( )
A.?150°???B.?75°???C.?60°????D.?15°
8.下列命题中,不正确的是( )
A.圆是轴对称图形 B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形 D.以上都不对
9.若⊙O内一条弦把圆周分为3∶1的两段弧,且⊙O的半径为R,那么这条弦的长为( )
A.R B.2R C.R D.R
10..如图,已知EF是⊙O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与⊙O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止.设∠POF=x,则x的取值范围是(???? )
A.30≤x≤60???B.30≤x≤90??C.30≤x≤120??D.60≤x≤120
2、填空题
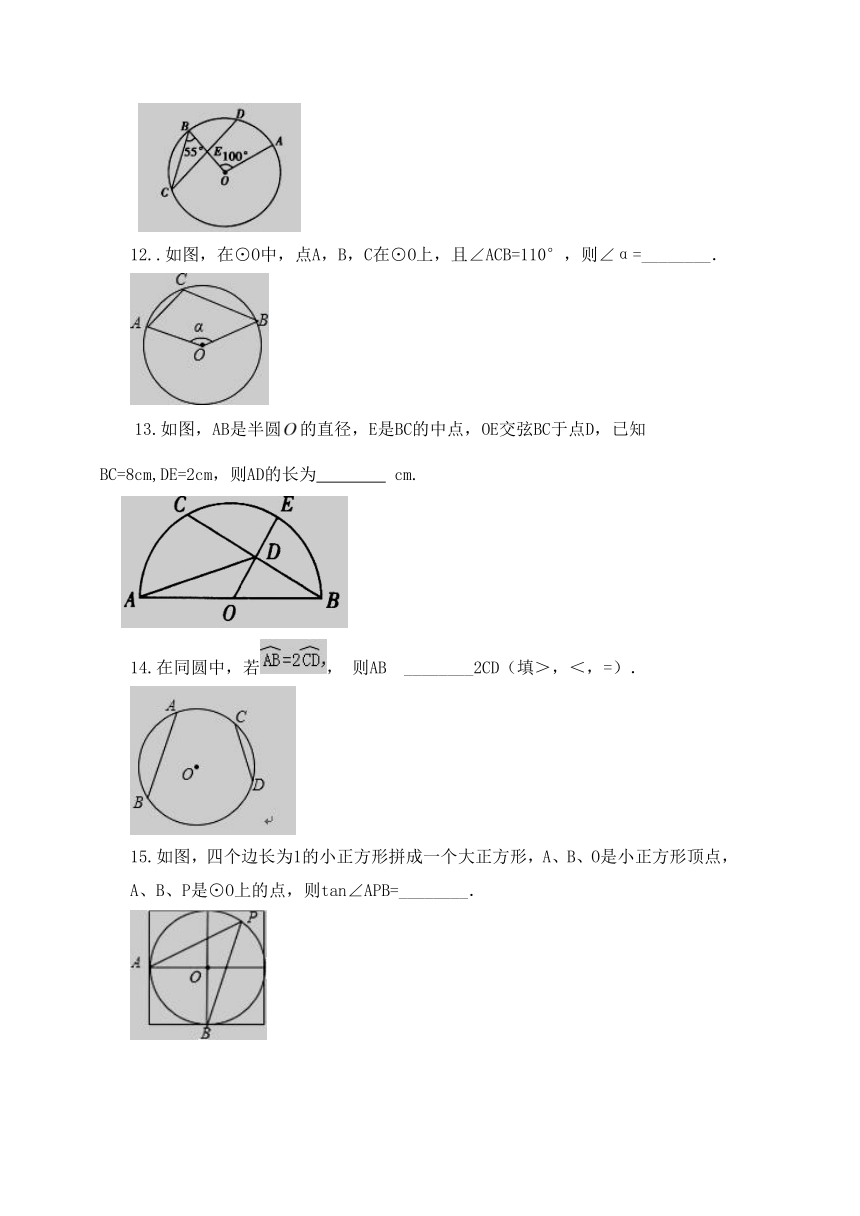
11.如图,A、B、C、D是⊙上四点,且D是AB的中点,CD交OB于E,,= 度.
12..如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=________.
13.如图,AB是半圆的直径,E是BC的中点,OE交弦BC于点D,已知BC=8cm,DE=2cm,则AD的长为 cm.
14.在同圆中,若, 则AB?________2CD(填>,<,=).
15.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O是小正方形顶点,A、B、P是⊙O上的点,则tan∠APB=________.
3、综合题
16.如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
17.储油罐截面直径650mm,装入一些油后,若油面宽AB=600mm,求油的最大深度.
18.我们已经知道在⊙O中,如果2∠AOB=∠COD,则CD=2AB,那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
19..如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。
(1)求证:∠DAC=∠BAC;
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
3.2 圆的对称性
同步测试答案
1、选择题
1.B 2.D 3.D 4.A 5.C 6.A 7.B 8.C 9.C 10.A
二、填空题
11.800
12.1400
13.2
14.<
15.
三、综合题
16.证明:∵AB=CD,
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
17.200mm
18.解:CD=2AB不成立.理由如下:
取的中点E,连接OE,CE,DE.
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
19.?(1)证明:如解图,连接OC,
则OC=OA,
∴∠BAC=∠OCA,
∵EF切⊙O于点C,
∴OC⊥EF,
∵AD⊥EF,
∴OC∥AD,
∴∠OCA=∠DAC,
∴∠DAC=∠BAC;
(2)解:如解图,连接BC,
∵AB是⊙O的直径,AD⊥EF,
∴∠ACB=∠ADC=90°,
由(Ⅰ)知∠DAC=∠BAC,
∴△ADC∽△ACB,
∴AC2=AD?AB=3×4=12,
∴AC=2,
在Rt△ABC中,cos∠BAC=,
∴∠BAC=30°?.?
?
⌒ ⌒
