选修2-3 人教A版 独立性检验的基本思想及其初步 课件(47张PPT)
文档属性
| 名称 | 选修2-3 人教A版 独立性检验的基本思想及其初步 课件(47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 09:43:54 | ||
图片预览









文档简介
(共47张PPT)
3.2
独立性检验的基本思想及其初步应用
主题 独立性检验
为了研究人的性别与患色盲是否有关系,某研究所进行
了随机调查,发现在调查的480名男性中有39名患有色
盲,520名女性中有6名患有色盲,能在犯错误的概率不
超过0.01的前提下认为人的性别与患色盲有关系吗?
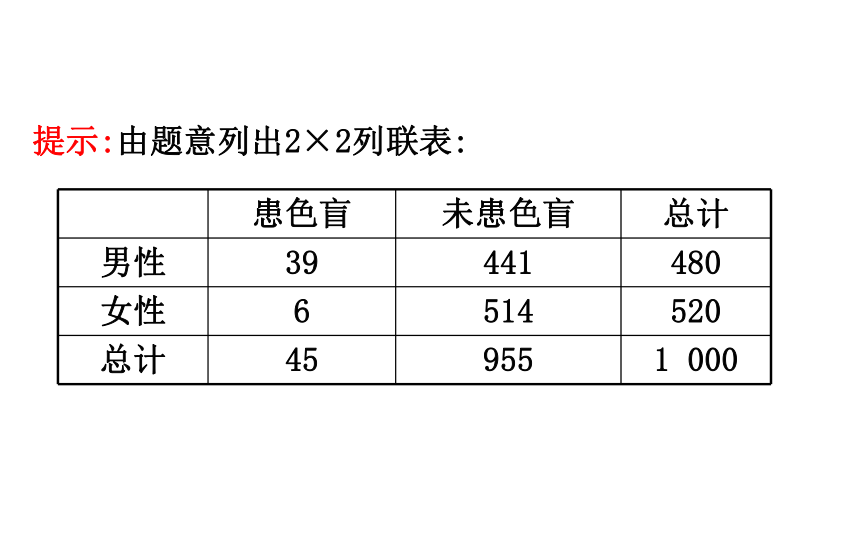
提示:由题意列出2×2列联表:
患色盲 未患色盲 总计
男性 39 441 480
女性 6 514 520
总计 45 955 1 000
由公式得K2的观测值为
k= ≈28.225.
因为k≥6.635,所以有99%的把握认为人的性别与患色
盲有关系,即在犯错误的概率不超过0.01的前提下认为
患色盲与人的性别有关系,男性患色盲的概率要比女性
大得多.
结论:
1.与列联表相关的概念
(1)分类变量:变量的不同“___”表示个体所属的___
_______,像这样的变量称为分类变量.
(2)列联表:
①列出的_____分类变量的_______,称为列联表.
值
不
同类别
两个
频数表
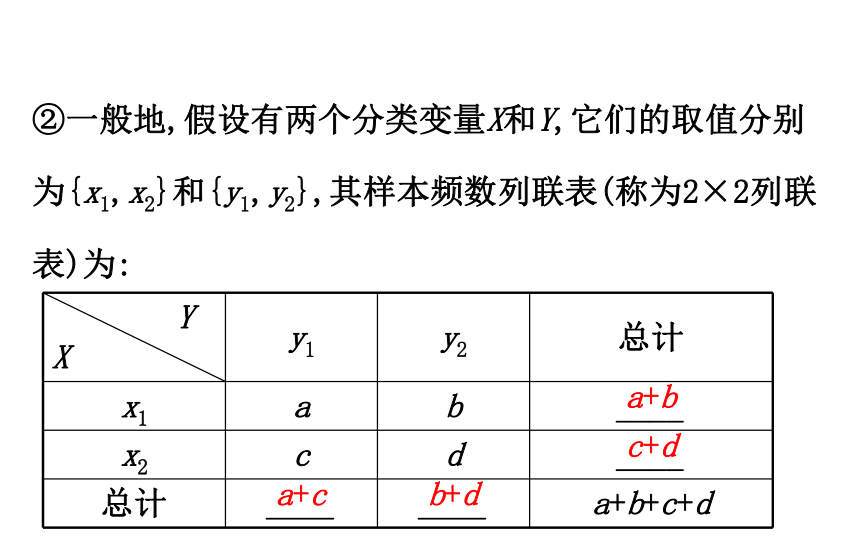
②一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
a+b
c+d
a+c
b+d
Y
X y1 y2 总计
x1 a b ____
x2 c d ____
总计 ____ ____ a+b+c+d
2.等高条形图
等高条形图与表格相比,图形更能直观地反映出两个分
类变量间是否_________,常用等高条形图展示列表数据
的_________.
相互影响
频率特征
3.独立性检验的基本思想
(1)定义:利用随机变量__来判断“两个分类变量_____
___”的方法称为独立性检验.
(2)公式:K2=____________________,其中n=________.
K2
有关
系
a+b+c+d
(3)独立性检验的具体做法:
①根据实际问题的需要确定容许推断“两个分类变量
有关系”犯错误概率的上界α,然后查表确定_______k0.
②利用公式计算随机变量K2的_______k.
临界值
观测值
③如果_____,就推断“X与Y有关系”,这种推断犯错误
的概率不超过α;否则,就认为在_____________不超过
α的前提下不能推断“X与Y有关系”,或者在样本数据
中_________________支持结论“X与Y有关系”.
k≥k0
犯错误的概率
没有发现足够证据
【对点训练】
1.分类变量X和Y的列联表如下,则 ( )
y1 y2 总 计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
A.ad-bc越小,说明X与Y的关系越弱
B.ad-bc越大,说明X与Y的关系越强
C.(ad-bc)2越大,说明X与Y的关系越强
D.(ad-bc)2越接近于0,说明X与Y的关系越强
【解析】选C.独立性检验主要根据的是 来判断,
若 越大,说明两者关系越强,反之就越弱.
2.调查在2~3级风的海上航行中男女乘客的晕船情况,结果如表所示:
晕船 不晕船 总计
男人 12 25 37
女人 10 24 34
总计 22 49 71
根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?
【解析】假设H0:海上航行晕船和性别没有关系,
K2的观测值k= ≈0.08.
因为k2<3.841,所以我们没有理由认为在2~3级风的海
上航行男人比女人更容易晕船.
类型一 2×2列联表和K2统计量
【典例1】根据下表计算:
K2的观测值k≈________.(结果保留3位小数)?
不看电视 看电视
男 37 85
女 35 143
【解题指南】利用K2= 准确代
数与计算,求出K2的值.
【解析】K2的观测值k=
答案:4.514
【方法总结】独立性检验的两个关注点
(1)独立性检验的关键是正确列出2×2列联表,并计算出K2的值.
(2)弄清判断两变量有关的把握性与犯错误概率的关系,根据题目要求进行正确的回答.
【跟踪训练】
某研究中心为研究是否喜欢数学课与性别的关系得到2×2列联表如表:
喜欢数学课 不喜欢数学课 总计
男生 60 20 80
女生 10 10 20
总计 70 30 100
参考公式:K2= ,其中n=a+b+c+d.
则随机变量K2的观测值约为 ( )
A.9.524 B.4.762
C.0.011 9 D.0.023 8
【解析】选B.由题意可得K2=
= ≈4.762 .
类型二 独立性检验
【典例2】某市为迎接“国家义务教育均衡发展”综合
评估,市教育行政部门在全市范围内随机抽取了n所学
校,并组织专家对两个必检指标进行考核评分.其中x,y
分别表示“学校的基础设施建设”和“学校的师资力
量”两项指标,根据评分将每项指标划分为A(优秀)、
B(良好)、C(及格)三个等级,调查结果如表所示.例如:表中“学校的基础设施建设”指标为B等级的共有20+21+2=43所学校.已知两项指标均为B等级的概率为0.21.
x
y A B C
A 20 20 1
B 12 21 1
C a 2 b
(1)在该样本中,若“学校的基础设施建设”优秀率是0.4,请填写下面2×2列联表,并根据列联表判断能否在犯错误的概率不超过0.10的前提下认为“学校的基础设施建设”和“学校的师资力量”有关;
师资力量(优秀) 师资力量(非优秀) 总计
基础设施建设
(优秀)
基础设施建设
(非优秀)
总计
(2)在该样本的“学校的师资力量”为C等级的学校中,若a≥18,11≤b≤15,记随机变量ξ=|a-b|,求ξ的分布列和数学期望.
附:K2=
P 0.15 0.10 0.050 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
【解题指南】(1)依题意求得n、a、b的值,填写2×2列联表,计算K2的值,对照临界值可得出答案;
(2)由题意得到满足条件的(a,b),再计算可得ξ的分布列和数学期望.
【解析】(1)依题意得 =0.21,得n=100,
由 =0.4,得a=8,
由20+20+1+12+21+1+a+2+b=100,得b=15,
2×2列联表如下:
师资力量(优秀) 师资力量(非优秀) 总计
基础设施建设(优秀) 20 20 40
基础设施建设(非优秀) 21 39 60
总计 41 59 100
K2= ≈2.232,
因为2.027<2.232<2.706,
所以不能在犯错误的概率不超过0.10的前提下认为“学校的基础设施建设”和“学校的师资力量”有关.
(2)由a≥8,11≤b≤15,得到满足条件的 有:
故ξ的分布列为
故E(ξ)=1×
【方法总结】运用独立性检验的方法
(1)列出2×2列联表,根据公式计算K2.
(2)根据临界值作出判断.
【跟踪训练】
1.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?
【解析】列出2×2列联表:
理 文 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
代入公式得k= ≈1.871×10-4.
因为1.871×10-4<3.841,可以认为学生选报文、理科
与对外语的兴趣无关.
2.为研究棉花种子经过处理跟生病之间的关系得到下表数据:
种子处理 种子未处理 总计
得病 32 101 133
不得病 61 213 274
总计 93 314 407
根据以上数据,则种子经过处理与是否生病________ (填“有”或“无”)关.?
【解析】由公式K2= ≈0.164 1<
2.706.所以种子经过处理与是否生病无关.
答案:无
3.为了解对人社部新的退休方案的关注程度,某机构选取“70后”和“80后”两个年龄段作为调查对象,进行了问卷调查,共调查了120名“80后”,80名“70后”,其中调查的“80后”有40名不关注,其余的全部关注;调查的“70后”有10人不关注,其余的全部关注.
(1)根据以上数据完成下列2×2列联表:
关注 不关注 总计
“80后”
“70后”
总计
(2)根据2×2列联表,能否在犯错误的概率不超过0.001
的前提下,认为“关注与年龄段有关”?请说明理由.
参考公式:K2= (n=a+b+c+d).
附表:
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
【解析】(1)2×2列联表:
关注 不关注 总计
“80后” 80 40 120
“70后” 70 10 80
总计 150 50 200
(2)根据列联表计算k= ≈11.11
>10.828.
对照观测值得:能在犯错误的概率不超过0.001的前提
下认为“关注与年龄段有关”.
【知识思维导图】
3.2
独立性检验的基本思想及其初步应用
主题 独立性检验
为了研究人的性别与患色盲是否有关系,某研究所进行
了随机调查,发现在调查的480名男性中有39名患有色
盲,520名女性中有6名患有色盲,能在犯错误的概率不
超过0.01的前提下认为人的性别与患色盲有关系吗?
提示:由题意列出2×2列联表:
患色盲 未患色盲 总计
男性 39 441 480
女性 6 514 520
总计 45 955 1 000
由公式得K2的观测值为
k= ≈28.225.
因为k≥6.635,所以有99%的把握认为人的性别与患色
盲有关系,即在犯错误的概率不超过0.01的前提下认为
患色盲与人的性别有关系,男性患色盲的概率要比女性
大得多.
结论:
1.与列联表相关的概念
(1)分类变量:变量的不同“___”表示个体所属的___
_______,像这样的变量称为分类变量.
(2)列联表:
①列出的_____分类变量的_______,称为列联表.
值
不
同类别
两个
频数表
②一般地,假设有两个分类变量X和Y,它们的取值分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:
a+b
c+d
a+c
b+d
Y
X y1 y2 总计
x1 a b ____
x2 c d ____
总计 ____ ____ a+b+c+d
2.等高条形图
等高条形图与表格相比,图形更能直观地反映出两个分
类变量间是否_________,常用等高条形图展示列表数据
的_________.
相互影响
频率特征
3.独立性检验的基本思想
(1)定义:利用随机变量__来判断“两个分类变量_____
___”的方法称为独立性检验.
(2)公式:K2=____________________,其中n=________.
K2
有关
系
a+b+c+d
(3)独立性检验的具体做法:
①根据实际问题的需要确定容许推断“两个分类变量
有关系”犯错误概率的上界α,然后查表确定_______k0.
②利用公式计算随机变量K2的_______k.
临界值
观测值
③如果_____,就推断“X与Y有关系”,这种推断犯错误
的概率不超过α;否则,就认为在_____________不超过
α的前提下不能推断“X与Y有关系”,或者在样本数据
中_________________支持结论“X与Y有关系”.
k≥k0
犯错误的概率
没有发现足够证据
【对点训练】
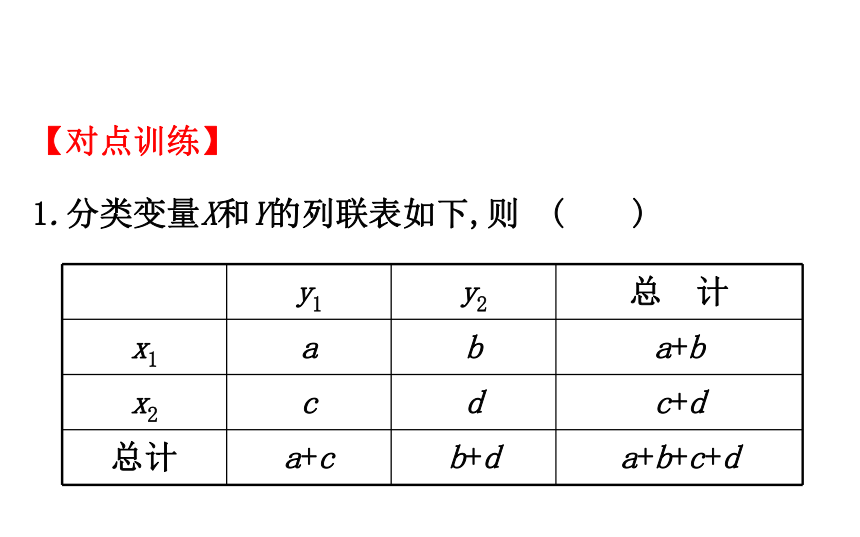
1.分类变量X和Y的列联表如下,则 ( )
y1 y2 总 计
x1 a b a+b
x2 c d c+d
总计 a+c b+d a+b+c+d
A.ad-bc越小,说明X与Y的关系越弱
B.ad-bc越大,说明X与Y的关系越强
C.(ad-bc)2越大,说明X与Y的关系越强
D.(ad-bc)2越接近于0,说明X与Y的关系越强
【解析】选C.独立性检验主要根据的是 来判断,
若 越大,说明两者关系越强,反之就越弱.
2.调查在2~3级风的海上航行中男女乘客的晕船情况,结果如表所示:
晕船 不晕船 总计
男人 12 25 37
女人 10 24 34
总计 22 49 71
根据此资料,你是否认为在2~3级风的海上航行中男人比女人更容易晕船?
【解析】假设H0:海上航行晕船和性别没有关系,
K2的观测值k= ≈0.08.
因为k2<3.841,所以我们没有理由认为在2~3级风的海
上航行男人比女人更容易晕船.
类型一 2×2列联表和K2统计量
【典例1】根据下表计算:
K2的观测值k≈________.(结果保留3位小数)?
不看电视 看电视
男 37 85
女 35 143
【解题指南】利用K2= 准确代
数与计算,求出K2的值.
【解析】K2的观测值k=
答案:4.514
【方法总结】独立性检验的两个关注点
(1)独立性检验的关键是正确列出2×2列联表,并计算出K2的值.
(2)弄清判断两变量有关的把握性与犯错误概率的关系,根据题目要求进行正确的回答.
【跟踪训练】
某研究中心为研究是否喜欢数学课与性别的关系得到2×2列联表如表:
喜欢数学课 不喜欢数学课 总计
男生 60 20 80
女生 10 10 20
总计 70 30 100
参考公式:K2= ,其中n=a+b+c+d.
则随机变量K2的观测值约为 ( )
A.9.524 B.4.762
C.0.011 9 D.0.023 8
【解析】选B.由题意可得K2=
= ≈4.762 .
类型二 独立性检验
【典例2】某市为迎接“国家义务教育均衡发展”综合
评估,市教育行政部门在全市范围内随机抽取了n所学
校,并组织专家对两个必检指标进行考核评分.其中x,y
分别表示“学校的基础设施建设”和“学校的师资力
量”两项指标,根据评分将每项指标划分为A(优秀)、
B(良好)、C(及格)三个等级,调查结果如表所示.例如:表中“学校的基础设施建设”指标为B等级的共有20+21+2=43所学校.已知两项指标均为B等级的概率为0.21.
x
y A B C
A 20 20 1
B 12 21 1
C a 2 b
(1)在该样本中,若“学校的基础设施建设”优秀率是0.4,请填写下面2×2列联表,并根据列联表判断能否在犯错误的概率不超过0.10的前提下认为“学校的基础设施建设”和“学校的师资力量”有关;
师资力量(优秀) 师资力量(非优秀) 总计
基础设施建设
(优秀)
基础设施建设
(非优秀)
总计
(2)在该样本的“学校的师资力量”为C等级的学校中,若a≥18,11≤b≤15,记随机变量ξ=|a-b|,求ξ的分布列和数学期望.
附:K2=
P 0.15 0.10 0.050 0.025 0.010
k0 2.072 2.706 3.841 5.024 6.635
【解题指南】(1)依题意求得n、a、b的值,填写2×2列联表,计算K2的值,对照临界值可得出答案;
(2)由题意得到满足条件的(a,b),再计算可得ξ的分布列和数学期望.
【解析】(1)依题意得 =0.21,得n=100,
由 =0.4,得a=8,
由20+20+1+12+21+1+a+2+b=100,得b=15,
2×2列联表如下:
师资力量(优秀) 师资力量(非优秀) 总计
基础设施建设(优秀) 20 20 40
基础设施建设(非优秀) 21 39 60
总计 41 59 100
K2= ≈2.232,
因为2.027<2.232<2.706,
所以不能在犯错误的概率不超过0.10的前提下认为“学校的基础设施建设”和“学校的师资力量”有关.
(2)由a≥8,11≤b≤15,得到满足条件的 有:
故ξ的分布列为
故E(ξ)=1×
【方法总结】运用独立性检验的方法
(1)列出2×2列联表,根据公式计算K2.
(2)根据临界值作出判断.
【跟踪训练】
1.为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?
【解析】列出2×2列联表:
理 文 总计
有兴趣 138 73 211
无兴趣 98 52 150
总计 236 125 361
代入公式得k= ≈1.871×10-4.
因为1.871×10-4<3.841,可以认为学生选报文、理科
与对外语的兴趣无关.
2.为研究棉花种子经过处理跟生病之间的关系得到下表数据:
种子处理 种子未处理 总计
得病 32 101 133
不得病 61 213 274
总计 93 314 407
根据以上数据,则种子经过处理与是否生病________ (填“有”或“无”)关.?
【解析】由公式K2= ≈0.164 1<
2.706.所以种子经过处理与是否生病无关.
答案:无
3.为了解对人社部新的退休方案的关注程度,某机构选取“70后”和“80后”两个年龄段作为调查对象,进行了问卷调查,共调查了120名“80后”,80名“70后”,其中调查的“80后”有40名不关注,其余的全部关注;调查的“70后”有10人不关注,其余的全部关注.
(1)根据以上数据完成下列2×2列联表:
关注 不关注 总计
“80后”
“70后”
总计
(2)根据2×2列联表,能否在犯错误的概率不超过0.001
的前提下,认为“关注与年龄段有关”?请说明理由.
参考公式:K2= (n=a+b+c+d).
附表:
P(K2≥k0) 0.050 0.010 0.001
k0 3.841 6.635 10.828
【解析】(1)2×2列联表:
关注 不关注 总计
“80后” 80 40 120
“70后” 70 10 80
总计 150 50 200
(2)根据列联表计算k= ≈11.11
>10.828.
对照观测值得:能在犯错误的概率不超过0.001的前提
下认为“关注与年龄段有关”.
【知识思维导图】
