2019-2020学年上海市青浦区东方中学八年级(上)期中数学试卷解析版
文档属性
| 名称 | 2019-2020学年上海市青浦区东方中学八年级(上)期中数学试卷解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 116.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-11 06:54:31 | ||
图片预览




文档简介
2019-2020学年上海市青浦区东方中学八年级(上)期中数学试卷
一、选择题(共8分,每题2分)
1.(2分)下列方程中,关于x的一元二次方程是( )
A.3(x+1)2=2(x+1) B.
C.ax2+bx+c=0 D.x2+2x=x2﹣1
2.(2分)下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等
B.两直线平行,内错角相等
C.全等三角形三条对应边相等
D.全等三角形的周长相等
3.(2分)如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
A.24° B.30° C.32° D.36°
4.(2分)在函数y=(k>0)的图象上有三点A1(x1,y1)、A2(x2,y2)、A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是( )
A.y1<0<y2 B.y3<0<y1 C.y2<y1<y3 D.y3<y1<y2
二、填空题(共28分,每题2分)
5.(2分)方程5x=x2的根是 .
6.(2分)已知m是方程x2﹣2x﹣1=0的根,则m(m﹣2)的值是 .
7.(2分)一元二次方程x2﹣mx﹣2=0的根的情况是 .
8.(2分)在实数范围内分解因式x2+2x﹣4= .
9.(2分)函数的定义域是 .
10.(2分)已知,那么f(6)= .
11.(2分)受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2016年利润为2亿元,2018年利润为2.88亿元.设平均利润增长率为x,则依题意列出方程为 .
12.(2分)反比例函数的图象位于 象限.
13.(2分)A(﹣1,3)在正比例函数y=kx图象上,则y随着x的增大而 .
14.(2分)已知双曲线y=经过点A(a,a+4)和点B(2a,2a﹣1),则a的值是 .
15.(2分)在△ABC中,∠C=90°,DE是AB边上的垂直平分线,交BC于点E,若∠EAC:∠EAB=5:2,则∠B= °.
16.(2分)如图,DE、FG分别是△ABC的AB、AC边上的垂直平分线,且∠BAC=100°,那么∠DAF的度数为 °.
17.(2分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE= .
18.(2分)如图,点A在双曲线y=上,点B在双曲线y=上,且AB‖x轴,过点A、B分别向x轴作垂线,垂足分别为点D、C,那么四边形ABCD的面积是 .
三、解答题(共25分,19、20、21每题5分,22题4分,23题6分)
19.(5分)解方程:x2﹣2x+1=0.
20.(5分)用配方法解方程:2x2﹣6x﹣1=0
21.(5分)解方程:4(x+3)2=25(x﹣2)2.
22.(4分)表示汽车性能的参数有很多,例如:长宽高、轴距、排量、功率、扭矩、转速、百公里油耗等等.为了了解某种车的耗油量,某专业检测人员对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
邮箱剩余油量Q(L)
100
94
88
82
…
①根据上表可知,每小时耗油 升;
②根据上表的数据,写出用Q与t的关系式: ;
③汽车油箱中剩余油量为55L,则汽车行驶了 小时.
23.(6分)已知y=y1+y2,并且y1与(x﹣1)成正比例,y2与x成反比例.当x=2时,y=5;当x=﹣2时,y=﹣9.求y关于x的函数解析式.
四、简答题(共39分,24、25、26每题6分,27、28、29每题7分)
24.(6分)如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米,在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?
25.(6分)关于x的一元二次方程mx2﹣(3m﹣1)x+2m﹣1=0,其根的判别式的值为1,求m的值及该方程的解.
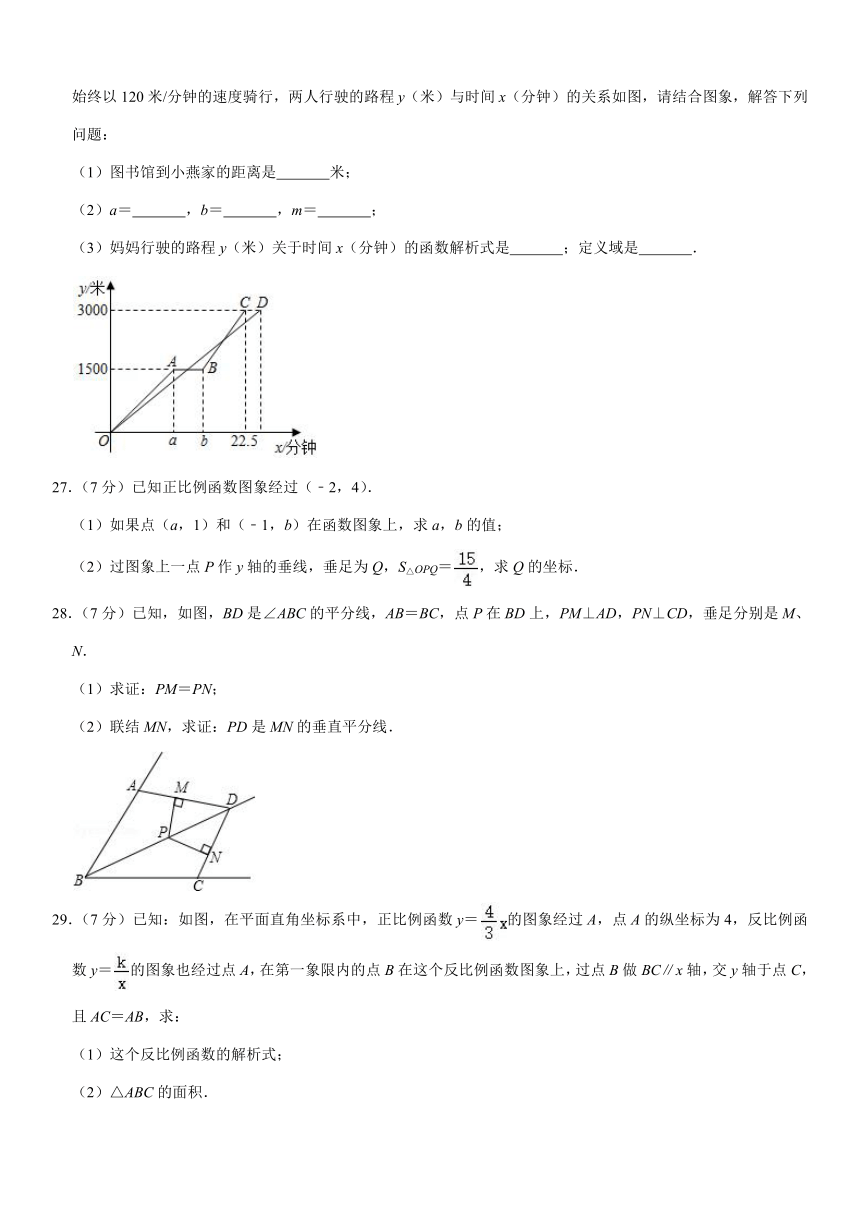
26.(6分)为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .
27.(7分)已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=,求Q的坐标.
28.(7分)已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
29.(7分)已知:如图,在平面直角坐标系中,正比例函数y=的图象经过A,点A的纵坐标为4,反比例函数y=的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
(1)这个反比例函数的解析式;
(2)△ABC的面积.
2019-2020学年上海市青浦区东方中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共8分,每题2分)
1.【解答】解:
A、3(x+1)2=2(x+1)化简得3x2+4x+1=0,是一元二次方程,故正确;
B、方程不是整式方程,故错误;
C、若a=0,则就不是一元二次方程,故错误;
D、是一元一次方程,故错误.
故选:A.
2.【解答】解:A、等腰三角形的两个底角相等的逆命题是两个底角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、“两直线平行,内错角相等”的逆命题是“内错角相等,两直线平行”是真命题,故不符合题意;
C、“全等三角形对应边相等”的逆命题是“三边对应相等的两个三角形全等”是真命题,故不符合题意;
D、“全等三角形的周长相等”的逆命题是“周长相等的三角形全等”是假命题,故D符合题意;
故选:D.
3.【解答】解:∵EF是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∴∠ABD=∠DBC=∠ECB,
∵∠BAC=60°,∠ACE=24°,
∴∠ABD=∠DBC=∠ECB=(180°﹣60°﹣24°)=32°.
故选:C.
4.【解答】解:∵k>0,函数图象如图,
∴图象在第一、三象限,在每个象限内,y随x的增大而减小,
∵x1<x2<0<x3,
∴y2<y1<y3.
故选:C.
二、填空题(共28分,每题2分)
5.【解答】解:∵x2﹣5x=0,
∴x(x﹣5)=0,
则x=0或x﹣5=0,
解得x1=0,x2=5,
故答案为:x1=0,x2=5.
6.【解答】解:∵m是方程x2﹣2x﹣1=0的根,
∴m2﹣2m﹣1=0,
∴m2﹣2m=1,
∴m(m﹣2)=m2﹣2m=1.
故答案是:1.
7.【解答】解:a=1,b=﹣m,c=﹣2,
△=b2﹣4ac=(﹣m)2﹣4×1×(﹣2)=m2+8.
∵m2≥0,
∴m2+8>0,
∴一元二次方程x2﹣mx﹣2=0有两个不相等的实根.
故答案为:有两个不相等的实根.
8.【解答】解:x2+2x﹣4=(x+1+)(x+1﹣),
故答案为:(x+1+)(x+1﹣).
9.【解答】解:根据题意得:x≥0且2x﹣4≠0,
解得:x≥0且x≠2.
故答案为:x≥0且x≠2.
10.【解答】解:f(6)===2.
故答案为:2.
11.【解答】解:设年平均增长率为x,则2017年利润为2(1+x)亿元,2018利润为2(1+x)2.
那么可得方程:2(1+x)2=2.88.
故答案是:2(1+x)2=2.88.
12.【解答】解:∵反比例函数y=中,k=2>0,
∴函数的图象位于一、三象限.
13.【解答】解:把A(﹣1,3)代入y=kx得:3=﹣k,
∴k=﹣3<0,
∴y随x的增大而减小.
故答案为:减小.
14.【解答】解:∵双曲线y=经过点A(a,a+4)和点B(2a,2a﹣1),
∴a≠0,
根据题意得k=a(a+4)=2a(2a﹣1),
解得a=2和a=0(舍去),
故答案为2.
15.【解答】解:连接AE,如图所示.
∵DE是AB边上的垂直平分线,
∴AE=DE,
∴∠B=∠EAB.
∵∠EAC:∠EAB=5:2,∠BAC=∠EAC+∠EAB,
∴∠BAC=∠B+∠B=∠B.
∵在△ABC中,∠C=90°,
∴∠B+∠BAC=90°,即∠B+∠B=90°,
∴∠B=20°.
故答案为:20.
16.【解答】解:由三角形内角和定理得,∠B+∠C=180°﹣∠BAC=180°﹣100°=80°,
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
同理可知,∠FAC=∠C,
∴∠DAF=∠BAC﹣(∠DAB+∠FAC)=∠BAC﹣(∠B+∠C)=20°,
故答案为:20.
17.【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC面积是45cm2,
∴×16?DE+×14?DF=45,
解得DE=3cm.
故答案为:3.
18.【解答】解:过点A作AE⊥y轴于点E,
∵点A在双曲线y=上,点B在双曲线y=上,
∴矩形EODA的面积为:1,矩形EOCB的面积是3,
∴矩形ABCD的面积为:3﹣1=2,
故答案为2.
三、解答题(共25分,19、20、21每题5分,22题4分,23题6分)
19.【解答】解:x2﹣2x+1=0,
∵a=1,b=﹣2,c=1,
∴x===±1;
∴x1=+1,x2=﹣1.
20.【解答】解:∵2x2﹣6x=1,
∴x2﹣3x=,
∴x2﹣3x+=+,即(x﹣)2=,
∴x﹣=±,
则x1=,x2=.
21.【解答】解:4(x+3)2=25(x﹣2)2,
开方得:2(x+3)=±5(x﹣2),
解得:,.
22.【解答】解:(1)据上表可知,每小时耗油100﹣94=6 升;
(2)关键题意得:Q=100﹣6t;
(3)当Q=55时,55=100﹣6t,
6t=45,
t=7.5.
答:汽车行使了7.5小时.
故答案为:①6;②Q=100﹣6t;③7.5.
23.【解答】解:
由题意可设y1=k(x﹣1),y2=,
∴y=y1+y2=k(x﹣1)+,
把x=2,y=5;x=﹣2,y=﹣9代入可得,解得,
∴y关于x的函数解析式为y=2(x﹣1)+.
四、简答题(共39分,24、25、26每题6分,27、28、29每题7分)
24.【解答】解:设垂直于墙的一边长为x米,则平行于墙的一边长为(32﹣2x+2)米,
由题意得x?(32﹣2x+2)=140,
整理,得x2﹣17x+70=0,
解得x1=10,x2=7,
当垂直于墙的边长为7米,则平行于墙的长度为32﹣14+2=20(米)>16米,舍去;
当垂直于墙的边长为10米,则平行于墙的长度为32﹣20+2=14(米);
答:仓库的长和宽分别为10米,14米.
25.【解答】解:由题意知,m≠0,△=b2﹣4ac=[﹣(3m﹣1)]2﹣4m(2m﹣1)=1
∴m1=0(舍去),m2=2,∴原方程化为:2x2﹣5x+3=0,
解得,x1=1,x2=3/2.
26.【解答】解:(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为:3000;
(2)a=1500÷150=10,
b=a+5=10+5=15,
m=(3000﹣1500)÷(22.5﹣15)=200,
故答案为:10,15,200;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=kx,
当y=3000时,x=3000÷120=25,
则3000=25k,得k=120,
即妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=120x,定义域是0≤x≤25,
故答案为:y=120x,0≤x≤25.
27.【解答】解:(1)设正比比例函数的解析式为y=kx(k≠0),
∵正比例函数图象经过(﹣2,4),
∴4=﹣2k,
解得k=﹣2,
∴正比例函数的解析式为y=﹣2x.
∵点(a,1)和(﹣1,b)在函数图象上,
∴1=﹣2a,b=﹣1×(﹣2),
解得a=﹣,b=2;
(2)设P(x,﹣2x),则Q(0,﹣2x),
∵S△OPQ=,
∴﹣x(﹣2x)=,
解得x=±,
∴Q(0,)或(0,).
28.【解答】证明:(1)∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN;
(2)在Rt△PDM和Rt△PDN中,
,
∴Rt△PDM≌Rt△PDN(HL),
∴DM=DN,
∴D在MN的垂直平分线上,
∵PM=PN,
∴P在MN的垂直平分线上,
∴PD是MN的垂直平分线.
29.【解答】解:(1)把点A的纵坐标4,代入正比例函数y=得,
x=3,
∴A(3,4)代入反比例函数y=得,
k=3×4=12,
因此,反比例函数的关系式为y=;
(2)如图,过点A作AM⊥x轴,垂足为M,交BC于点N,
∵BC∥x轴,
∴AM⊥BC,
∵AB=AC,
∴CN=NB=3,
∴BC=3+3=6,
当x=6时,y==2,
∴点B(6,2),
∵AN=AM﹣MN=4﹣2=2,
∴S△ABC=BC?AN=×6×2=6,
一、选择题(共8分,每题2分)
1.(2分)下列方程中,关于x的一元二次方程是( )
A.3(x+1)2=2(x+1) B.
C.ax2+bx+c=0 D.x2+2x=x2﹣1
2.(2分)下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等
B.两直线平行,内错角相等
C.全等三角形三条对应边相等
D.全等三角形的周长相等
3.(2分)如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )
A.24° B.30° C.32° D.36°
4.(2分)在函数y=(k>0)的图象上有三点A1(x1,y1)、A2(x2,y2)、A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是( )
A.y1<0<y2 B.y3<0<y1 C.y2<y1<y3 D.y3<y1<y2
二、填空题(共28分,每题2分)
5.(2分)方程5x=x2的根是 .
6.(2分)已知m是方程x2﹣2x﹣1=0的根,则m(m﹣2)的值是 .
7.(2分)一元二次方程x2﹣mx﹣2=0的根的情况是 .
8.(2分)在实数范围内分解因式x2+2x﹣4= .
9.(2分)函数的定义域是 .
10.(2分)已知,那么f(6)= .
11.(2分)受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高.据统计,2016年利润为2亿元,2018年利润为2.88亿元.设平均利润增长率为x,则依题意列出方程为 .
12.(2分)反比例函数的图象位于 象限.
13.(2分)A(﹣1,3)在正比例函数y=kx图象上,则y随着x的增大而 .
14.(2分)已知双曲线y=经过点A(a,a+4)和点B(2a,2a﹣1),则a的值是 .
15.(2分)在△ABC中,∠C=90°,DE是AB边上的垂直平分线,交BC于点E,若∠EAC:∠EAB=5:2,则∠B= °.
16.(2分)如图,DE、FG分别是△ABC的AB、AC边上的垂直平分线,且∠BAC=100°,那么∠DAF的度数为 °.
17.(2分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是45cm2,AB=16cm,AC=14cm,则DE= .
18.(2分)如图,点A在双曲线y=上,点B在双曲线y=上,且AB‖x轴,过点A、B分别向x轴作垂线,垂足分别为点D、C,那么四边形ABCD的面积是 .
三、解答题(共25分,19、20、21每题5分,22题4分,23题6分)
19.(5分)解方程:x2﹣2x+1=0.
20.(5分)用配方法解方程:2x2﹣6x﹣1=0
21.(5分)解方程:4(x+3)2=25(x﹣2)2.
22.(4分)表示汽车性能的参数有很多,例如:长宽高、轴距、排量、功率、扭矩、转速、百公里油耗等等.为了了解某种车的耗油量,某专业检测人员对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h)
0
1
2
3
…
邮箱剩余油量Q(L)
100
94
88
82
…
①根据上表可知,每小时耗油 升;
②根据上表的数据,写出用Q与t的关系式: ;
③汽车油箱中剩余油量为55L,则汽车行驶了 小时.
23.(6分)已知y=y1+y2,并且y1与(x﹣1)成正比例,y2与x成反比例.当x=2时,y=5;当x=﹣2时,y=﹣9.求y关于x的函数解析式.
四、简答题(共39分,24、25、26每题6分,27、28、29每题7分)
24.(6分)如图,要建一个面积为140平方米的仓库,仓库的一边靠墙,这堵墙长16米,在与墙平行的一边,要开一扇2米宽的门.已知围建仓库的现有木板材料可使新建板墙的总长为32米,那么这个仓库设计的长和宽应分别为多少米?
25.(6分)关于x的一元二次方程mx2﹣(3m﹣1)x+2m﹣1=0,其根的判别式的值为1,求m的值及该方程的解.
26.(6分)为了响应“低碳环保,绿色出行”的公益活动,小燕和妈妈决定周日骑自行车去图书馆借书.她们同时从家出发,小燕先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分钟的速度到达图书馆,而妈妈始终以120米/分钟的速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)图书馆到小燕家的距离是 米;
(2)a= ,b= ,m= ;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是 ;定义域是 .
27.(7分)已知正比例函数图象经过(﹣2,4).
(1)如果点(a,1)和(﹣1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q,S△OPQ=,求Q的坐标.
28.(7分)已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.
(1)求证:PM=PN;
(2)联结MN,求证:PD是MN的垂直平分线.
29.(7分)已知:如图,在平面直角坐标系中,正比例函数y=的图象经过A,点A的纵坐标为4,反比例函数y=的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
(1)这个反比例函数的解析式;
(2)△ABC的面积.
2019-2020学年上海市青浦区东方中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(共8分,每题2分)
1.【解答】解:
A、3(x+1)2=2(x+1)化简得3x2+4x+1=0,是一元二次方程,故正确;
B、方程不是整式方程,故错误;
C、若a=0,则就不是一元二次方程,故错误;
D、是一元一次方程,故错误.
故选:A.
2.【解答】解:A、等腰三角形的两个底角相等的逆命题是两个底角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、“两直线平行,内错角相等”的逆命题是“内错角相等,两直线平行”是真命题,故不符合题意;
C、“全等三角形对应边相等”的逆命题是“三边对应相等的两个三角形全等”是真命题,故不符合题意;
D、“全等三角形的周长相等”的逆命题是“周长相等的三角形全等”是假命题,故D符合题意;
故选:D.
3.【解答】解:∵EF是BC的垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD,
∴∠ABD=∠DBC=∠ECB,
∵∠BAC=60°,∠ACE=24°,
∴∠ABD=∠DBC=∠ECB=(180°﹣60°﹣24°)=32°.
故选:C.
4.【解答】解:∵k>0,函数图象如图,
∴图象在第一、三象限,在每个象限内,y随x的增大而减小,
∵x1<x2<0<x3,
∴y2<y1<y3.
故选:C.
二、填空题(共28分,每题2分)
5.【解答】解:∵x2﹣5x=0,
∴x(x﹣5)=0,
则x=0或x﹣5=0,
解得x1=0,x2=5,
故答案为:x1=0,x2=5.
6.【解答】解:∵m是方程x2﹣2x﹣1=0的根,
∴m2﹣2m﹣1=0,
∴m2﹣2m=1,
∴m(m﹣2)=m2﹣2m=1.
故答案是:1.
7.【解答】解:a=1,b=﹣m,c=﹣2,
△=b2﹣4ac=(﹣m)2﹣4×1×(﹣2)=m2+8.
∵m2≥0,
∴m2+8>0,
∴一元二次方程x2﹣mx﹣2=0有两个不相等的实根.
故答案为:有两个不相等的实根.
8.【解答】解:x2+2x﹣4=(x+1+)(x+1﹣),
故答案为:(x+1+)(x+1﹣).
9.【解答】解:根据题意得:x≥0且2x﹣4≠0,
解得:x≥0且x≠2.
故答案为:x≥0且x≠2.
10.【解答】解:f(6)===2.
故答案为:2.
11.【解答】解:设年平均增长率为x,则2017年利润为2(1+x)亿元,2018利润为2(1+x)2.
那么可得方程:2(1+x)2=2.88.
故答案是:2(1+x)2=2.88.
12.【解答】解:∵反比例函数y=中,k=2>0,
∴函数的图象位于一、三象限.
13.【解答】解:把A(﹣1,3)代入y=kx得:3=﹣k,
∴k=﹣3<0,
∴y随x的增大而减小.
故答案为:减小.
14.【解答】解:∵双曲线y=经过点A(a,a+4)和点B(2a,2a﹣1),
∴a≠0,
根据题意得k=a(a+4)=2a(2a﹣1),
解得a=2和a=0(舍去),
故答案为2.
15.【解答】解:连接AE,如图所示.
∵DE是AB边上的垂直平分线,
∴AE=DE,
∴∠B=∠EAB.
∵∠EAC:∠EAB=5:2,∠BAC=∠EAC+∠EAB,
∴∠BAC=∠B+∠B=∠B.
∵在△ABC中,∠C=90°,
∴∠B+∠BAC=90°,即∠B+∠B=90°,
∴∠B=20°.
故答案为:20.
16.【解答】解:由三角形内角和定理得,∠B+∠C=180°﹣∠BAC=180°﹣100°=80°,
∵DE是线段AB的垂直平分线,
∴DA=DB,
∴∠DAB=∠B,
同理可知,∠FAC=∠C,
∴∠DAF=∠BAC﹣(∠DAB+∠FAC)=∠BAC﹣(∠B+∠C)=20°,
故答案为:20.
17.【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC面积是45cm2,
∴×16?DE+×14?DF=45,
解得DE=3cm.
故答案为:3.
18.【解答】解:过点A作AE⊥y轴于点E,
∵点A在双曲线y=上,点B在双曲线y=上,
∴矩形EODA的面积为:1,矩形EOCB的面积是3,
∴矩形ABCD的面积为:3﹣1=2,
故答案为2.
三、解答题(共25分,19、20、21每题5分,22题4分,23题6分)
19.【解答】解:x2﹣2x+1=0,
∵a=1,b=﹣2,c=1,
∴x===±1;
∴x1=+1,x2=﹣1.
20.【解答】解:∵2x2﹣6x=1,
∴x2﹣3x=,
∴x2﹣3x+=+,即(x﹣)2=,
∴x﹣=±,
则x1=,x2=.
21.【解答】解:4(x+3)2=25(x﹣2)2,
开方得:2(x+3)=±5(x﹣2),
解得:,.
22.【解答】解:(1)据上表可知,每小时耗油100﹣94=6 升;
(2)关键题意得:Q=100﹣6t;
(3)当Q=55时,55=100﹣6t,
6t=45,
t=7.5.
答:汽车行使了7.5小时.
故答案为:①6;②Q=100﹣6t;③7.5.
23.【解答】解:
由题意可设y1=k(x﹣1),y2=,
∴y=y1+y2=k(x﹣1)+,
把x=2,y=5;x=﹣2,y=﹣9代入可得,解得,
∴y关于x的函数解析式为y=2(x﹣1)+.
四、简答题(共39分,24、25、26每题6分,27、28、29每题7分)
24.【解答】解:设垂直于墙的一边长为x米,则平行于墙的一边长为(32﹣2x+2)米,
由题意得x?(32﹣2x+2)=140,
整理,得x2﹣17x+70=0,
解得x1=10,x2=7,
当垂直于墙的边长为7米,则平行于墙的长度为32﹣14+2=20(米)>16米,舍去;
当垂直于墙的边长为10米,则平行于墙的长度为32﹣20+2=14(米);
答:仓库的长和宽分别为10米,14米.
25.【解答】解:由题意知,m≠0,△=b2﹣4ac=[﹣(3m﹣1)]2﹣4m(2m﹣1)=1
∴m1=0(舍去),m2=2,∴原方程化为:2x2﹣5x+3=0,
解得,x1=1,x2=3/2.
26.【解答】解:(1)由图象可得,
图书馆到小燕家的距离是3000米,
故答案为:3000;
(2)a=1500÷150=10,
b=a+5=10+5=15,
m=(3000﹣1500)÷(22.5﹣15)=200,
故答案为:10,15,200;
(3)妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=kx,
当y=3000时,x=3000÷120=25,
则3000=25k,得k=120,
即妈妈行驶的路程y(米)关于时间x(分钟)的函数解析式是y=120x,定义域是0≤x≤25,
故答案为:y=120x,0≤x≤25.
27.【解答】解:(1)设正比比例函数的解析式为y=kx(k≠0),
∵正比例函数图象经过(﹣2,4),
∴4=﹣2k,
解得k=﹣2,
∴正比例函数的解析式为y=﹣2x.
∵点(a,1)和(﹣1,b)在函数图象上,
∴1=﹣2a,b=﹣1×(﹣2),
解得a=﹣,b=2;
(2)设P(x,﹣2x),则Q(0,﹣2x),
∵S△OPQ=,
∴﹣x(﹣2x)=,
解得x=±,
∴Q(0,)或(0,).
28.【解答】证明:(1)∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN;
(2)在Rt△PDM和Rt△PDN中,
,
∴Rt△PDM≌Rt△PDN(HL),
∴DM=DN,
∴D在MN的垂直平分线上,
∵PM=PN,
∴P在MN的垂直平分线上,
∴PD是MN的垂直平分线.
29.【解答】解:(1)把点A的纵坐标4,代入正比例函数y=得,
x=3,
∴A(3,4)代入反比例函数y=得,
k=3×4=12,
因此,反比例函数的关系式为y=;
(2)如图,过点A作AM⊥x轴,垂足为M,交BC于点N,
∵BC∥x轴,
∴AM⊥BC,
∵AB=AC,
∴CN=NB=3,
∴BC=3+3=6,
当x=6时,y==2,
∴点B(6,2),
∵AN=AM﹣MN=4﹣2=2,
∴S△ABC=BC?AN=×6×2=6,
同课章节目录
