人教版七年级下册数学8.2消元法解二元一次方程组(1)课件(20张PPT )
文档属性
| 名称 | 人教版七年级下册数学8.2消元法解二元一次方程组(1)课件(20张PPT ) |

|
|
| 格式 | zip | ||
| 文件大小 | 863.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 08:57:42 | ||
图片预览





文档简介
(共18张PPT)
消元——解二元一次方程组(1)
——代入消元法
学习目标 :
1、会用代入法解二元一次方程组。
2、体会解二元一次方程组的基本思想——“消元”。
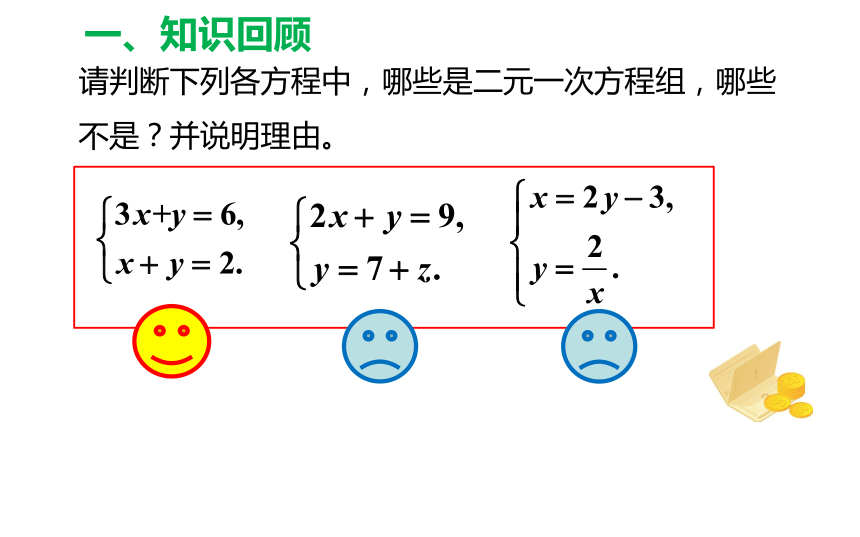
一、知识回顾
请判断下列各方程中,哪些是二元一次方程组,哪些不是?并说明理由。
二元一次方程组的解:
二元一次方程组 的解是( )
A.
B.
C.
D.
C
方程的解:使方程两边相等的未知数的值。
方程组的解:两个方程的公共解。
二、创设情境 导入新课
(列方程解应用题)篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
解:设胜x场,则负(10-x)场,根据题意得:
2x+ (10-x) =16
解得:x=6
∴负:10-6=4场
答:胜6场,负4场。
解:设篮球队胜了x场,负了y场。根据题意得方程组
x+y = 10
2x+y =16
x + y=10 ①
2x+y=16 ②
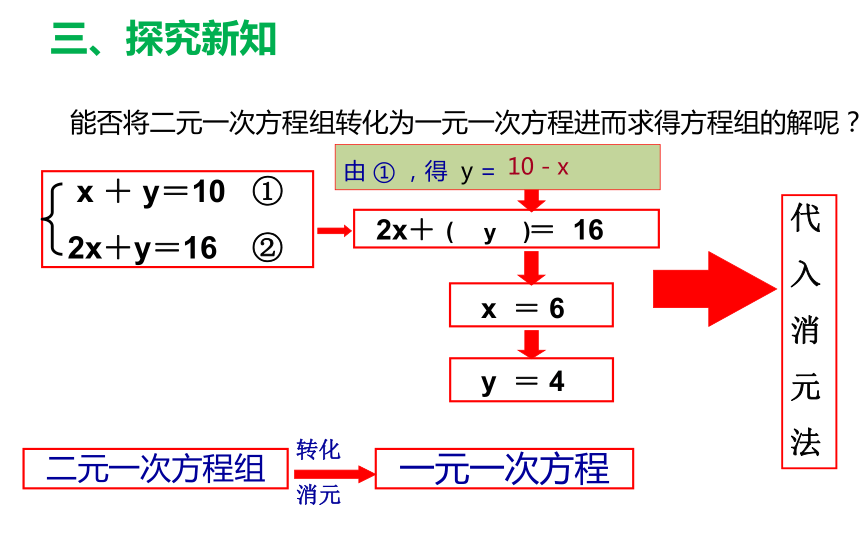
能否将二元一次方程组转化为一元一次方程进而求得方程组的解呢?
2x+ y = 16
x = 6
二元一次方程组
一元一次方程
消元
由 ① ,得 y = 10 - x
转化
代
入
消
元
法
y = 4
10 - x
( )
三、探究新知
二元一次方程组中有两个未知数,如果消去其中的一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程。我们可以先解出一个未知数,然后再求另一个未知数。这种将未知数的个数有多化少、逐一解决的想法,叫做消元思想。
消元思想
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法。
归 纳:
把下列方程写成用一个未知数表示另一个未知数的形式。
(1) x-y=3
试一试
或
解:y=x-3
x=3+y
把③代入①可以吗?试试看?
把y=-1代入①
或②可以吗?
注意:方程组解的书
写形式
由某一方程转化的方
程必须代入另一个
方程.
例1 用代入法解方程组
代入方程③简单
代入哪一个方程
较简便呢?
变形
代入
求解
回代
写解
用大括号括起来
所以这个方程组的解是
x = 2,
y =-1.
把y=-1代入③,得 x=2.
解这个方程,得 y=-1.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x = y + 3 . ③
由①得,-y = 3 - x
y = x-3
点拔:灵活选择要表示的未知数,一般选择系数较简单的那个
方程进行转化。
问题2:请同学们比较转化后方程你有什么发现?
问题1:(1)对于方程①你能用含x的式子表示y吗?
(2)对于方程②你能用含y的式 子表示x吗?
由②得,3x= 8y +14
说明 :
x-y=3
用y表示x
x = y+3
解方程组
①
②
我也来试一试
回顾我们学的知识
哪种方法解二元一次方程组?
1
思想方法?
3
代入消元法的步骤?
2
变形→代入→求解→回代→写解→检验
代入消元法
消元思想
最为简单的方法是将________式中________表示为 ,再代入__________
①
②
1、用代入法解二元一次方程组
随堂练习
D
2、用代入法解方程组
下列解法中最简便的是( )
A. 由 ① 得 代入②
B. 由① 得 代入②
C. 由② 得 代入①
D. 由②得 代入①
3.解二元一次方程组:
y-2x=0
⑴
x+y=12
(2)
5x-2y=-1
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
解得 x=4
把x=4代入③,得 y=8
∴原方程组的解是
解:由①,得
3x+7=2y ③
把x=3代入③ ,得 y=8
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
解得 x=4
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
把x=4代入③,得 y=8
∴原方程组的解是
解得 x=4
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
把③代入② ,得 5x-(3x+7)=-1
x=3
①
②
①
②
∴原方程组的解是
代入法也可以整体代入。
基本思想
步骤
方法
二元一次方
程组的解法
数学思想
消元
变形
代入法
回代
求解
代入
转化
写解
课堂小结
课后作业:
课本93页T1、T2、T3、T4
消元——解二元一次方程组(1)
——代入消元法
学习目标 :
1、会用代入法解二元一次方程组。
2、体会解二元一次方程组的基本思想——“消元”。
一、知识回顾
请判断下列各方程中,哪些是二元一次方程组,哪些不是?并说明理由。
二元一次方程组的解:
二元一次方程组 的解是( )
A.
B.
C.
D.
C
方程的解:使方程两边相等的未知数的值。
方程组的解:两个方程的公共解。
二、创设情境 导入新课
(列方程解应用题)篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?
解:设胜x场,则负(10-x)场,根据题意得:
2x+ (10-x) =16
解得:x=6
∴负:10-6=4场
答:胜6场,负4场。
解:设篮球队胜了x场,负了y场。根据题意得方程组
x+y = 10
2x+y =16
x + y=10 ①
2x+y=16 ②
能否将二元一次方程组转化为一元一次方程进而求得方程组的解呢?
2x+ y = 16
x = 6
二元一次方程组
一元一次方程
消元
由 ① ,得 y = 10 - x
转化
代
入
消
元
法
y = 4
10 - x
( )
三、探究新知
二元一次方程组中有两个未知数,如果消去其中的一个未知数,那么就把二元一次方程组转化为我们熟悉的一元一次方程。我们可以先解出一个未知数,然后再求另一个未知数。这种将未知数的个数有多化少、逐一解决的想法,叫做消元思想。
消元思想
上面的解法,是由二元一次方程组中一个方程,将一个未知数用含另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫代入消元法,简称代入法。
归 纳:
把下列方程写成用一个未知数表示另一个未知数的形式。
(1) x-y=3
试一试
或
解:y=x-3
x=3+y
把③代入①可以吗?试试看?
把y=-1代入①
或②可以吗?
注意:方程组解的书
写形式
由某一方程转化的方
程必须代入另一个
方程.
例1 用代入法解方程组
代入方程③简单
代入哪一个方程
较简便呢?
变形
代入
求解
回代
写解
用大括号括起来
所以这个方程组的解是
x = 2,
y =-1.
把y=-1代入③,得 x=2.
解这个方程,得 y=-1.
把③代入②,得 3(y+3)-8y=14.
解:由①,得 x = y + 3 . ③
由①得,-y = 3 - x
y = x-3
点拔:灵活选择要表示的未知数,一般选择系数较简单的那个
方程进行转化。
问题2:请同学们比较转化后方程你有什么发现?
问题1:(1)对于方程①你能用含x的式子表示y吗?
(2)对于方程②你能用含y的式 子表示x吗?
由②得,3x= 8y +14
说明 :
x-y=3
用y表示x
x = y+3
解方程组
①
②
我也来试一试
回顾我们学的知识
哪种方法解二元一次方程组?
1
思想方法?
3
代入消元法的步骤?
2
变形→代入→求解→回代→写解→检验
代入消元法
消元思想
最为简单的方法是将________式中________表示为 ,再代入__________
①
②
1、用代入法解二元一次方程组
随堂练习
D
2、用代入法解方程组
下列解法中最简便的是( )
A. 由 ① 得 代入②
B. 由① 得 代入②
C. 由② 得 代入①
D. 由②得 代入①
3.解二元一次方程组:
y-2x=0
⑴
x+y=12
(2)
5x-2y=-1
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
解得 x=4
把x=4代入③,得 y=8
∴原方程组的解是
解:由①,得
3x+7=2y ③
把x=3代入③ ,得 y=8
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
解得 x=4
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
把x=4代入③,得 y=8
∴原方程组的解是
解得 x=4
解:由①,得 y=2x ③
把③代入②,得 x+2x=12
把③代入② ,得 5x-(3x+7)=-1
x=3
①
②
①
②
∴原方程组的解是
代入法也可以整体代入。
基本思想
步骤
方法
二元一次方
程组的解法
数学思想
消元
变形
代入法
回代
求解
代入
转化
写解
课堂小结
课后作业:
课本93页T1、T2、T3、T4
