人教版数学七年级下册5.2平行线及其判定 课件(28张)
文档属性
| 名称 | 人教版数学七年级下册5.2平行线及其判定 课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
第五章 相交线与平行线
---5.2平行线及其判定
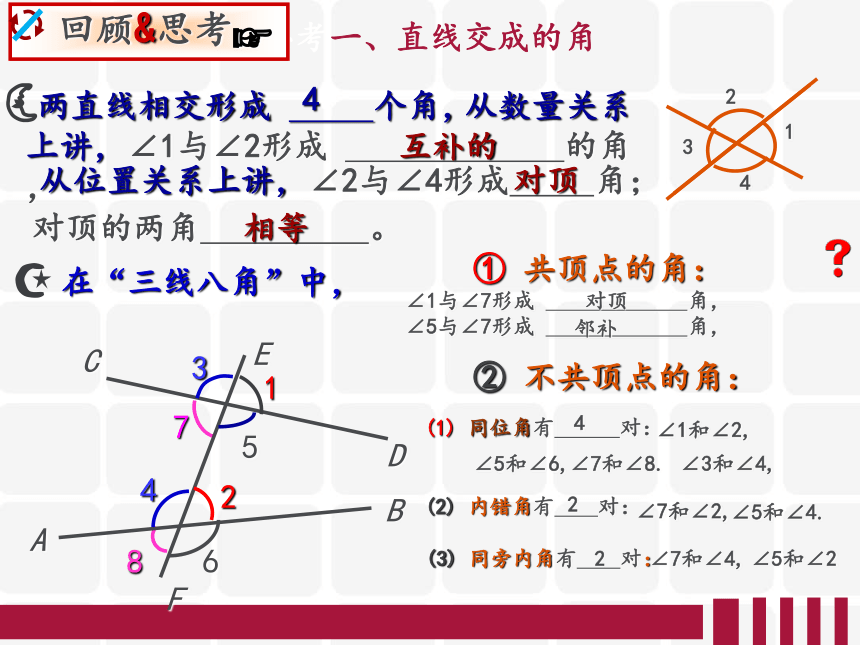
回顾与思考一、直线交成的角
两直线相交形成 个角,
1
2
3
4
互补的
从位置关系上讲,∠2与∠4形成 角;
对顶
① 共顶点的角:
∠1与∠7形成 角,
∠5与∠7形成 角,
② 不共顶点的角:
4
从数量关系上讲,∠1与∠2形成 的角,
对顶的两角 。
相等
对顶
邻补
(1) 同位角有 对:
4
(2) 内错角有 对:
2
(3) 同旁内角有 对:
2
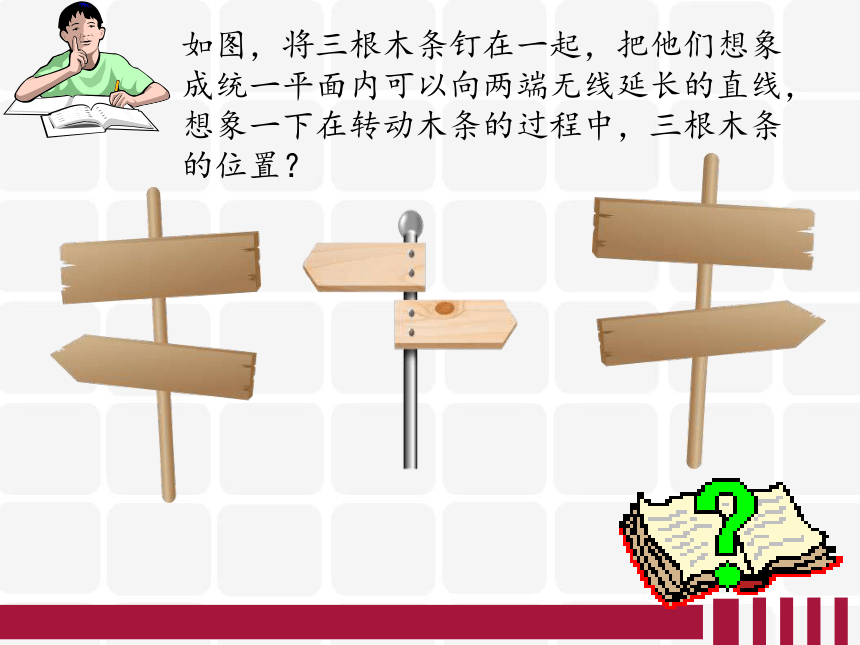
如图,将三根木条钉在一起,把他们想象成统一平面内可以向两端无线延长的直线,想象一下在转动木条的过程中,三根木条的位置?
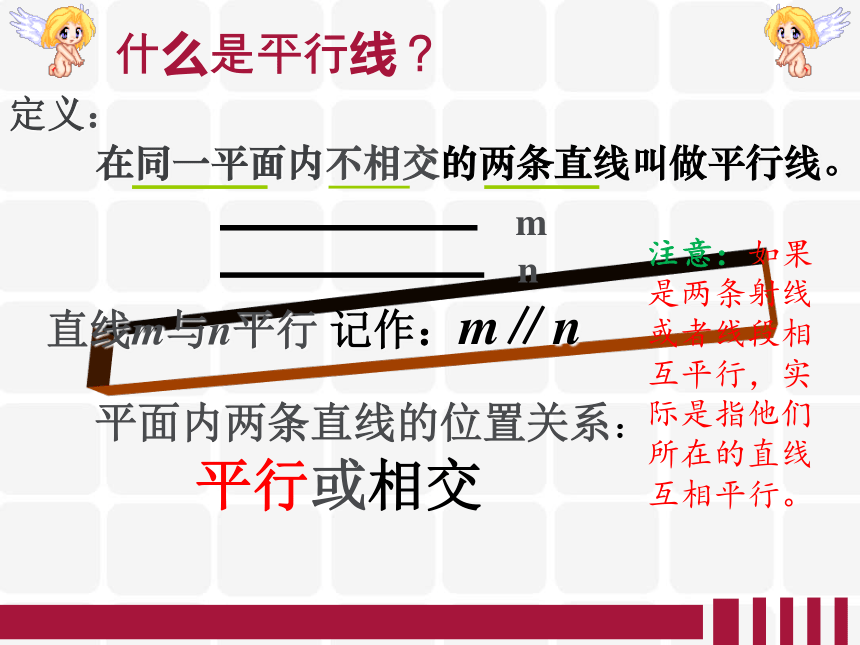
什么是平行线?
在同一平面内不相交的两条直线叫做平行线。
直线m与n平行 记作:m∥n
m
n
定义:
平面内两条直线的位置关系:
平行或相交
注意:如果是两条射线或者线段相互平行,实际是指他们所在的直线互相平行。
定义:
在同一平面内不相交的两条直线叫做平行线。
直线ɑ与b相互平行,记作 。
在同一平面内不重合的两条直线有 种位置关系,分别是 。
表示方法:
位置关系:
ɑ∥b
2
相交和平行
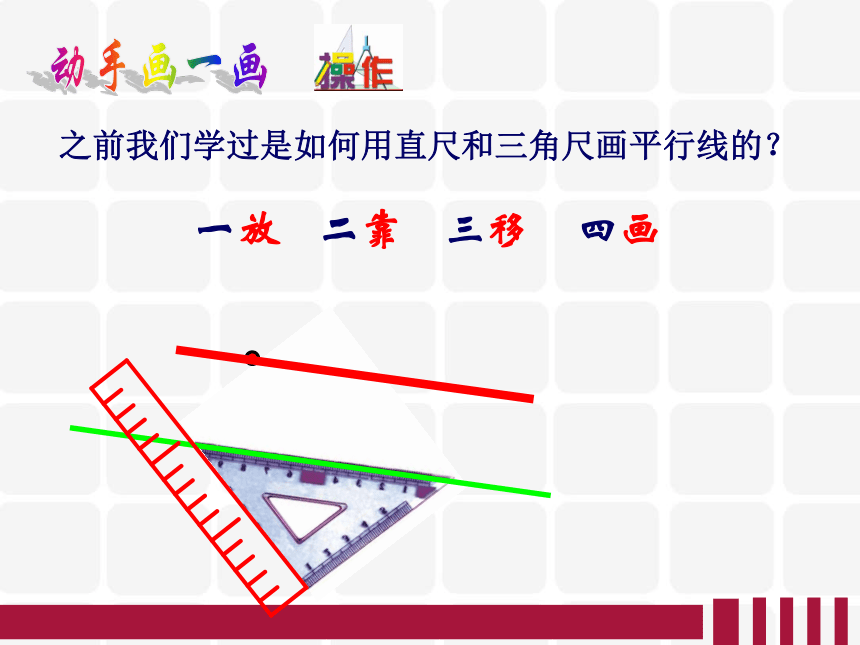
之前我们学过是如何用直尺和三角尺画平行线的?
一放
二靠
四画
三移
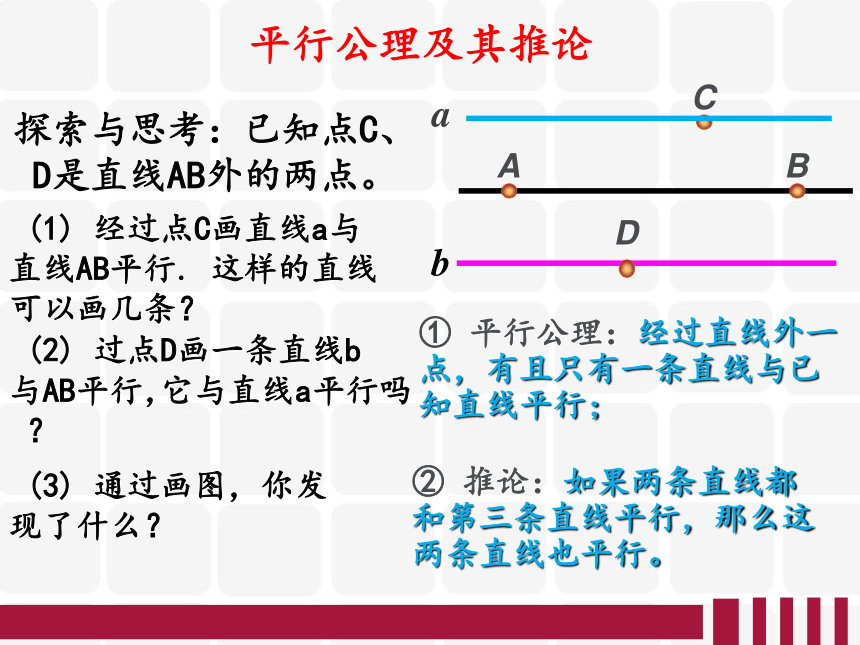
平行公理及其推论
它与直线a平行吗?
(3) 通过画图,你发现了什么?
① 平行公理:经过直线外一点,有且只有一条直线与已知直线平行;
② 推论:如果两条直线都和第三条直线平行,那么这两条直线也平行。
探索与思考:已知点C、D是直线AB外的两点。
注意:
(1)公理中“经过直线外一点”作平行线,当点在直线上时,作不出已知直线的平行线。
(2)“有且只有”中“有”表示存在,“只有”表示唯一,即有一条并且只有一条。
例题:
【例1】判断下列说法的正误
(1)在同一平面内,两条直线不平行就相交。
(2)在同一平面内,两条线段不平行就相交。
答案:(1)正确 (2)错误
【例2】下列说法正确的是( )
A.过一点有且只有一条直线与已知 直线平行。
B.在同一平面内,过一点有且只有一条直线与已知直线垂直。
C.因为a∥b,c∥d,所以a∥d。
D.一条直线的平行线只有一条。
B
根据下列要求画图。
(1)如图(1),过点A画MN∥BC.
(2)如图(2),过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H.
(3)如图(3),过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB延长线交于点F。
用直尺和三角尺画平行线的方法
一放
二靠
四画
三移
1.图中哪些线段互相平行?请分别将它们表示出。
A
B
C
D
E
F
G
H
I
P
M
N
Q
AB∥CD,BC ∥DE,FG∥MN,PQ ∥HI
2.在方格纸中,经过线段AB外一点C仅用直尺画线段AB的平行线.
A
B
C
m
之前我们学过是如何用直尺和三角尺画平行线的?在这一过程中三角尺起着什么样的作用?
一放
二靠
四画
三移
我们可以看到画AB的平行线CD,实际上就是过点P画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角。这说明如果同位角相等,那么AB∥CD。
那么如何判定两条直线平行?
判定定理1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
两条直线被第三条直线所截,同时得到同位角、内错角、同旁内角。由同位角可以判定两条直线平行,那么能否利用内错角或者同旁内角来判定两条直线平行呢?如图,如果∠2=∠3,能否得出a∥b呢?
如图,因为∠2=∠3,又因为∠3=∠1(为什么?),所以∠1=∠2,所以根据“同位角相等,两直线平行”,所以a∥b。
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
根据以上方法,同理我们可以得到平行线的判定定理3.
“转化思想”
判定定理3:如果两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
探究
遇到一个新问题时,常常把它转化为一个已(或者已经解决)的问题。
例:在同一平面内,如果两条直线都垂直与同一条直线,那么这两条直线平行吗?为什么?
解:如图, ,
∠1=∠2=90°
b∥c
判 断:
1.不相交的两条直线叫做平行线。 ( )
2.在同一平面内不相交的两条线段叫平行线。( )
5.过一点有且只有一条直线与已知直线平行. ( )
4.在同一平面内不相交的两条直线叫平行线。 ( )
×
×
×
√
练习一
3.两条直线不相交就平行。 ( )
×
选择
(1)在同一平面内有三条直线,如果要使其中两条且只 有两条直线平行,那么它们 ( )
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 有三个交点
(2)在同一平面内有三条直线,它们的交点个数是 ( )A. 0或2 B. 0或3
C. 0或1 D. 0或1或2或3
C
D
练习二
练习三
A
B
C
D
E
F
1.如图,在三棱柱中,
(1)与AE平行的棱为____;
(3)图中有无既不平行又不相交的两条棱?
(2)图中平行的棱共有___对;
BF
6
如:AE与DF
请把它们表示出来.
练习四
2.如图,P是∠AOB外一点.
(1)过点P画直线PC∥OA,与OB相交于点C;
(2)过点P画直线PD∥OB,与OA的反向延长线相交于点D;
(4)你能说出四边形PCOD的名称吗?
·
A
O
B
·
C
D
·
P
(3)分别量出∠AOB、 ∠PCO、 ∠PDO、 ∠CPD的度数,你有什么发现?
练习五
2. 如图,点O是直线CD外一点,OA∥CD,OB∥CD,那么∠AOB是平角,为什么?
·
A
B
C
D
O
解:∵OA∥CD,OB∥CD,
即 点A、O、B在同一条直线上
∴ ∠AOB是平角
∴OA、OB表示同一条直线
(经过直线外一点,有且只有一条直线与已知直线平行)
练习六:
3. 如图,已知直线 a、b、c在同一平面内 a∥b, a与c相交于点A,那么b与c一定相交吗?为什么?
a
b
c
A
解:假如b与c不相交,
那么b∥c,
又由于a∥b,
所以a∥c,
这与a与c相交于点A相矛盾,
所以b与c一定相交。
练习七
1.如图,AB∥CD,E是AC的中点。
·
A
B
C
D
E
(1)读句画图:过E作EF∥AB交BD于点F;
(2)判断EF与CD的位置关系,并说明理由。
·
F
解:∵EF∥AB, CD∥AB,
∴ EF∥CD
(平行于同一条直线的两条直线平行)
Thanks
第五章 相交线与平行线
---5.2平行线及其判定
回顾与思考一、直线交成的角
两直线相交形成 个角,
1
2
3
4
互补的
从位置关系上讲,∠2与∠4形成 角;
对顶
① 共顶点的角:
∠1与∠7形成 角,
∠5与∠7形成 角,
② 不共顶点的角:
4
从数量关系上讲,∠1与∠2形成 的角,
对顶的两角 。
相等
对顶
邻补
(1) 同位角有 对:
4
(2) 内错角有 对:
2
(3) 同旁内角有 对:
2
如图,将三根木条钉在一起,把他们想象成统一平面内可以向两端无线延长的直线,想象一下在转动木条的过程中,三根木条的位置?
什么是平行线?
在同一平面内不相交的两条直线叫做平行线。
直线m与n平行 记作:m∥n
m
n
定义:
平面内两条直线的位置关系:
平行或相交
注意:如果是两条射线或者线段相互平行,实际是指他们所在的直线互相平行。
定义:
在同一平面内不相交的两条直线叫做平行线。
直线ɑ与b相互平行,记作 。
在同一平面内不重合的两条直线有 种位置关系,分别是 。
表示方法:
位置关系:
ɑ∥b
2
相交和平行
之前我们学过是如何用直尺和三角尺画平行线的?
一放
二靠
四画
三移
平行公理及其推论
它与直线a平行吗?
(3) 通过画图,你发现了什么?
① 平行公理:经过直线外一点,有且只有一条直线与已知直线平行;
② 推论:如果两条直线都和第三条直线平行,那么这两条直线也平行。
探索与思考:已知点C、D是直线AB外的两点。
注意:
(1)公理中“经过直线外一点”作平行线,当点在直线上时,作不出已知直线的平行线。
(2)“有且只有”中“有”表示存在,“只有”表示唯一,即有一条并且只有一条。
例题:
【例1】判断下列说法的正误
(1)在同一平面内,两条直线不平行就相交。
(2)在同一平面内,两条线段不平行就相交。
答案:(1)正确 (2)错误
【例2】下列说法正确的是( )
A.过一点有且只有一条直线与已知 直线平行。
B.在同一平面内,过一点有且只有一条直线与已知直线垂直。
C.因为a∥b,c∥d,所以a∥d。
D.一条直线的平行线只有一条。
B
根据下列要求画图。
(1)如图(1),过点A画MN∥BC.
(2)如图(2),过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H.
(3)如图(3),过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB延长线交于点F。
用直尺和三角尺画平行线的方法
一放
二靠
四画
三移
1.图中哪些线段互相平行?请分别将它们表示出。
A
B
C
D
E
F
G
H
I
P
M
N
Q
AB∥CD,BC ∥DE,FG∥MN,PQ ∥HI
2.在方格纸中,经过线段AB外一点C仅用直尺画线段AB的平行线.
A
B
C
m
之前我们学过是如何用直尺和三角尺画平行线的?在这一过程中三角尺起着什么样的作用?
一放
二靠
四画
三移
我们可以看到画AB的平行线CD,实际上就是过点P画与∠2相等的∠1,而∠2和∠1正是直线AB,CD被直线EF截得的同位角。这说明如果同位角相等,那么AB∥CD。
那么如何判定两条直线平行?
判定定理1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
两条直线被第三条直线所截,同时得到同位角、内错角、同旁内角。由同位角可以判定两条直线平行,那么能否利用内错角或者同旁内角来判定两条直线平行呢?如图,如果∠2=∠3,能否得出a∥b呢?
如图,因为∠2=∠3,又因为∠3=∠1(为什么?),所以∠1=∠2,所以根据“同位角相等,两直线平行”,所以a∥b。
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
根据以上方法,同理我们可以得到平行线的判定定理3.
“转化思想”
判定定理3:如果两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
探究
遇到一个新问题时,常常把它转化为一个已(或者已经解决)的问题。
例:在同一平面内,如果两条直线都垂直与同一条直线,那么这两条直线平行吗?为什么?
解:如图, ,
∠1=∠2=90°
b∥c
判 断:
1.不相交的两条直线叫做平行线。 ( )
2.在同一平面内不相交的两条线段叫平行线。( )
5.过一点有且只有一条直线与已知直线平行. ( )
4.在同一平面内不相交的两条直线叫平行线。 ( )
×
×
×
√
练习一
3.两条直线不相交就平行。 ( )
×
选择
(1)在同一平面内有三条直线,如果要使其中两条且只 有两条直线平行,那么它们 ( )
A. 没有交点 B. 只有一个交点
C. 有两个交点 D. 有三个交点
(2)在同一平面内有三条直线,它们的交点个数是 ( )A. 0或2 B. 0或3
C. 0或1 D. 0或1或2或3
C
D
练习二
练习三
A
B
C
D
E
F
1.如图,在三棱柱中,
(1)与AE平行的棱为____;
(3)图中有无既不平行又不相交的两条棱?
(2)图中平行的棱共有___对;
BF
6
如:AE与DF
请把它们表示出来.
练习四
2.如图,P是∠AOB外一点.
(1)过点P画直线PC∥OA,与OB相交于点C;
(2)过点P画直线PD∥OB,与OA的反向延长线相交于点D;
(4)你能说出四边形PCOD的名称吗?
·
A
O
B
·
C
D
·
P
(3)分别量出∠AOB、 ∠PCO、 ∠PDO、 ∠CPD的度数,你有什么发现?
练习五
2. 如图,点O是直线CD外一点,OA∥CD,OB∥CD,那么∠AOB是平角,为什么?
·
A
B
C
D
O
解:∵OA∥CD,OB∥CD,
即 点A、O、B在同一条直线上
∴ ∠AOB是平角
∴OA、OB表示同一条直线
(经过直线外一点,有且只有一条直线与已知直线平行)
练习六:
3. 如图,已知直线 a、b、c在同一平面内 a∥b, a与c相交于点A,那么b与c一定相交吗?为什么?
a
b
c
A
解:假如b与c不相交,
那么b∥c,
又由于a∥b,
所以a∥c,
这与a与c相交于点A相矛盾,
所以b与c一定相交。
练习七
1.如图,AB∥CD,E是AC的中点。
·
A
B
C
D
E
(1)读句画图:过E作EF∥AB交BD于点F;
(2)判断EF与CD的位置关系,并说明理由。
·
F
解:∵EF∥AB, CD∥AB,
∴ EF∥CD
(平行于同一条直线的两条直线平行)
Thanks
