人教版八年级数学下册19.1.1变量与函数(第1课时)课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册19.1.1变量与函数(第1课时)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 799.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 14:55:17 | ||
图片预览





文档简介
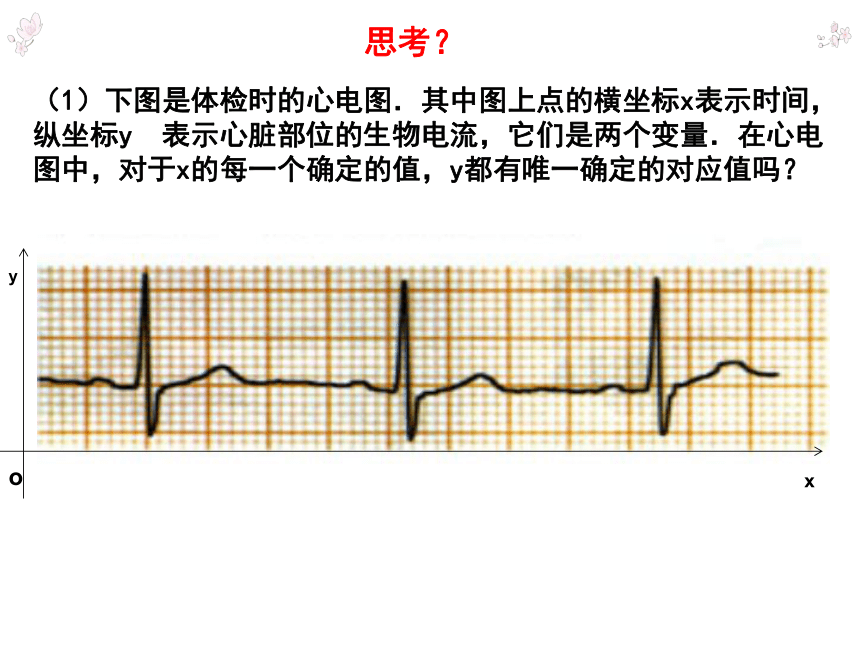
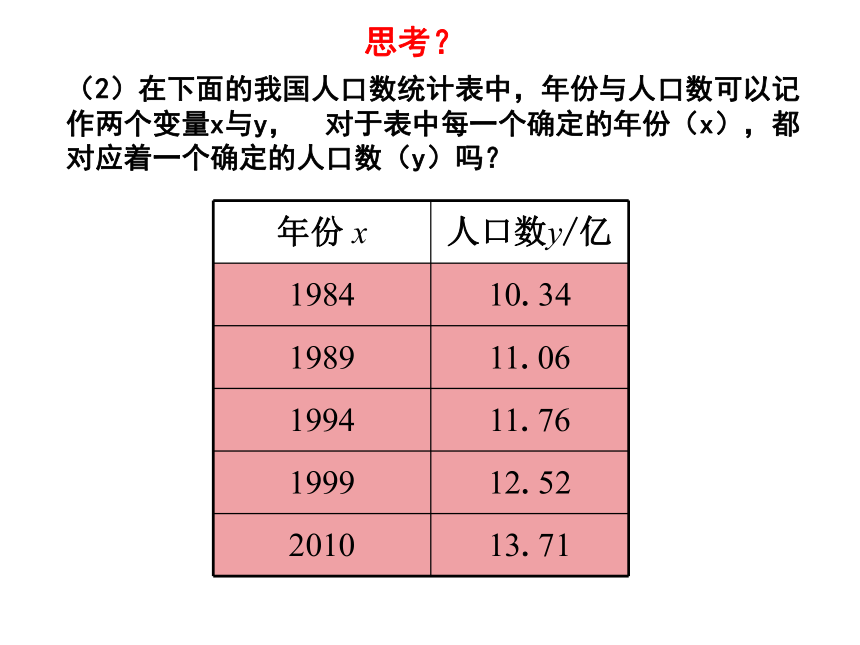
课件16张PPT。19.1.1 变量与函数(1)下图是体检时的心电图.其中图上点的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每一个确定的值,y都有唯一确定的对应值吗?oxy思考?(2)在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗?思考?问题:3、如果一个变量确定一个值时,另一个变量有唯一确定值与其对应吗?(1)s=60t;(2)y=10x;
(3)S=πr2;(4)y=5-x.2、如果一个变量发生变化,那么另一个变量随之发生变化吗?1、上面关系式有多少个变量? 函数是反映一个变化过程中的两个变量之间的一种特殊对应关系。 一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.1、函数是研究什么的呢?2、什么是函数和函数值? 如果x=a时y=b,那么b叫做当自变量的值为a时的函数值。 函数是反映一个变化过程中的两个变量之间的一种特殊对应关系。 一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.1、函数是研究什么的呢?2、什么是函数和函数值? 如果x=a时y=b,那么b叫做当自变量的值为a时的函数值。3、什么叫函数关系式? 描述自变量和函数之间的关系式叫函数关系式。
也叫函数解释式。例如:(1)s=60t;(2)y=10x;(3)S=πr2;(4)y=5-x.S=x2,S是x的函数,x是自变量;y=0.1x,y是x的函数,x是自变量;练习一1、改变正方形的边长 x,正方形的面积 S 随之变化;2、向一水池每分钟注水0.1 m3,注水量 y(单位:m3)随注水时间 x(单位:min)的变化而变化;下列问题中哪些量是自变量,哪些量是自变量的函数?
试写出函数的解释式。v=10-0.05t,v是t的函数,t是自变量.3、秀水村的耕地面积是106 m2,这个村人均占有耕
地面积 y (单位:m2)随这个村人数 n 的变化而变化;(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化。1、下列式子中的y是x的函数吗?为什么?练习二2、下列曲线中,表示y不是x的函数是( )B3、下图是一只蚂蚁在竖直的墙面上的爬行图,请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗?
为什么? 蚂蚁离起点的水平距离 t 是离地高度 h 的函数吗?
为什么?水平距离 t/cm 离地高度 h/cm 1 2 3 4 5 6 6
5
4
3
2
1讲例:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?解:(1)关系式为:y=50-0.1x;
(2) 0≤x≤500;
(3)∵当x=200时,y=50-0.1×200=30,
∴汽车行驶200 km时,油箱中还有30L汽油.练习三1、课本75页第2题2、求下列函数关系式的自变量的取值范围。3、我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.练习三 3. 甲、乙两辆汽车分别从相距200 km的A、B两地同时出发,相向而行,甲的平均速度为60 km/h,乙的平均速度为 40 km/h,当甲乙两车相遇时,两车都停止运动,设甲车的运动时间为x(h),甲、乙两车相距为y(km).
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)当甲车行驶1h时,两车相距多远?
(4)求当两车相距50 km时,甲车行驶的时间 .练习三作业课本82页第4、5题课本83页第10、11题
(3)S=πr2;(4)y=5-x.2、如果一个变量发生变化,那么另一个变量随之发生变化吗?1、上面关系式有多少个变量? 函数是反映一个变化过程中的两个变量之间的一种特殊对应关系。 一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.1、函数是研究什么的呢?2、什么是函数和函数值? 如果x=a时y=b,那么b叫做当自变量的值为a时的函数值。 函数是反映一个变化过程中的两个变量之间的一种特殊对应关系。 一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.1、函数是研究什么的呢?2、什么是函数和函数值? 如果x=a时y=b,那么b叫做当自变量的值为a时的函数值。3、什么叫函数关系式? 描述自变量和函数之间的关系式叫函数关系式。
也叫函数解释式。例如:(1)s=60t;(2)y=10x;(3)S=πr2;(4)y=5-x.S=x2,S是x的函数,x是自变量;y=0.1x,y是x的函数,x是自变量;练习一1、改变正方形的边长 x,正方形的面积 S 随之变化;2、向一水池每分钟注水0.1 m3,注水量 y(单位:m3)随注水时间 x(单位:min)的变化而变化;下列问题中哪些量是自变量,哪些量是自变量的函数?
试写出函数的解释式。v=10-0.05t,v是t的函数,t是自变量.3、秀水村的耕地面积是106 m2,这个村人均占有耕
地面积 y (单位:m2)随这个村人数 n 的变化而变化;(4)水池中有水10L,此后每小时漏水0.05L,水池中的水量V(单位:L)随时间t(单位:h)的变化而变化。1、下列式子中的y是x的函数吗?为什么?练习二2、下列曲线中,表示y不是x的函数是( )B3、下图是一只蚂蚁在竖直的墙面上的爬行图,请问:蚂蚁离地高度 h 是离起点的水平距离 t 的函数吗?
为什么? 蚂蚁离起点的水平距离 t 是离地高度 h 的函数吗?
为什么?水平距离 t/cm 离地高度 h/cm 1 2 3 4 5 6 6
5
4
3
2
1讲例:汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?解:(1)关系式为:y=50-0.1x;
(2) 0≤x≤500;
(3)∵当x=200时,y=50-0.1×200=30,
∴汽车行驶200 km时,油箱中还有30L汽油.练习三1、课本75页第2题2、求下列函数关系式的自变量的取值范围。3、我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.练习三 3. 甲、乙两辆汽车分别从相距200 km的A、B两地同时出发,相向而行,甲的平均速度为60 km/h,乙的平均速度为 40 km/h,当甲乙两车相遇时,两车都停止运动,设甲车的运动时间为x(h),甲、乙两车相距为y(km).
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)当甲车行驶1h时,两车相距多远?
(4)求当两车相距50 km时,甲车行驶的时间 .练习三作业课本82页第4、5题课本83页第10、11题
