人教版七年级数学下册10.1 统计调查课件(共59张PPT)
文档属性
| 名称 | 人教版七年级数学下册10.1 统计调查课件(共59张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 00:00:00 | ||
图片预览








文档简介
(共58张PPT)
10.1统计调查
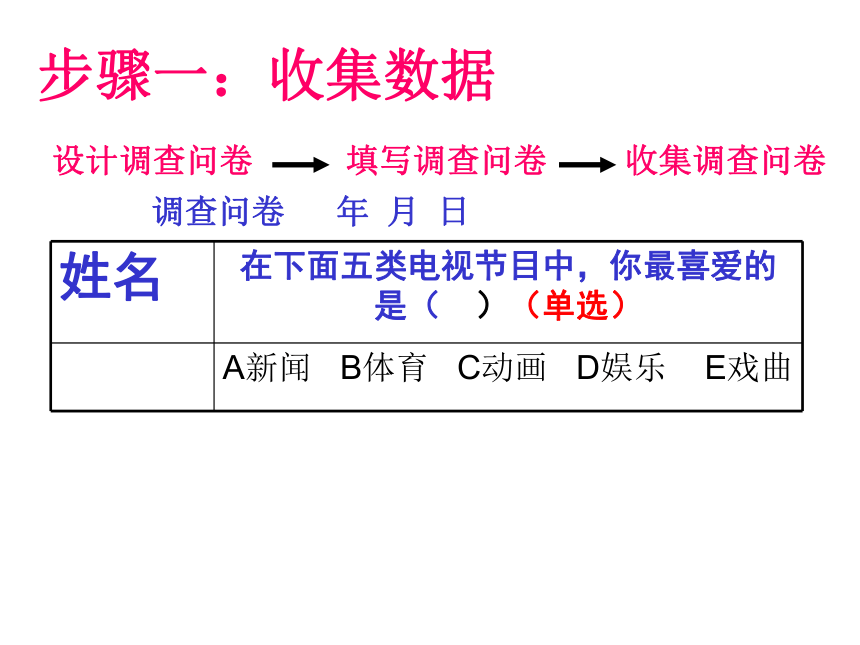
步骤一:收集数据
设计调查问卷
调查问卷 年 月 日
姓名 在下面五类电视节目中,你最喜爱的是( )(单选)
A新闻 B体育 C动画 D娱乐 E戏曲
填写调查问卷
收集调查问卷
问题1
某同学经调查,得到如下50个数据:
CCADBCADCD
CEABDDBCCC
DBDCDDDCDC
EBBDDCCEBD
ABDDCBCBDD
设计调查问卷
填写调查问卷
收集调查问卷
讨论1:从上面的数据中,你能看出全班同学喜爱各类节目的情况吗?怎样才能很清楚地看出全班同学喜爱各类节目的情况?
问题1
统计中经常用表格整理数据:
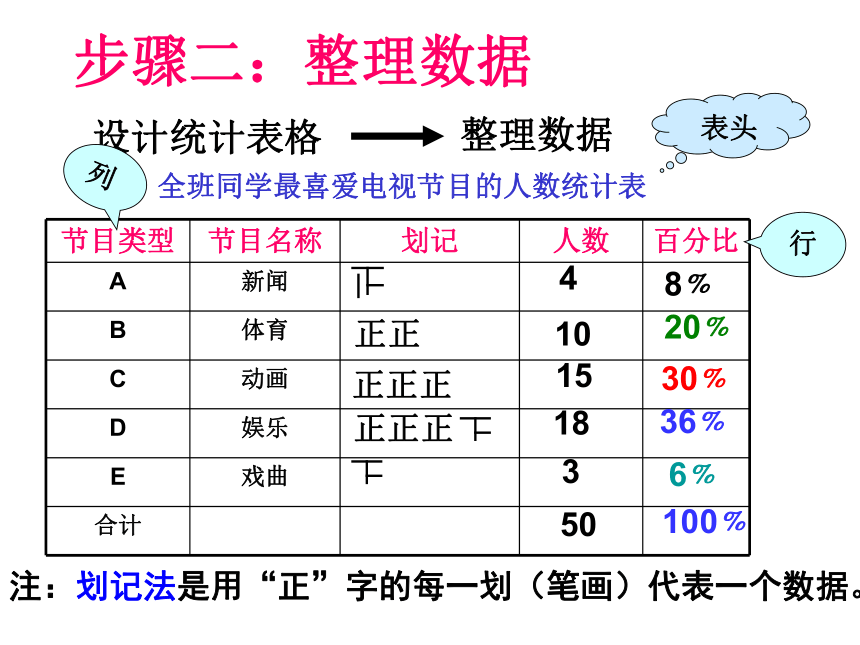
步骤二:整理数据
设计统计表格
整理数据
节目类型 节目名称 划记 人数 百分比
A 新闻
B 体育
C 动画
D 娱乐
E 戏曲
合计
全班同学最喜爱电视节目的人数统计表
表头
行
列
注:划记法是用“正”字的每一划(笔画)代表一个数据。
正正
正正正
正正正
4
10
15
18
3
50
8﹪
20﹪
30﹪
36﹪
6﹪
100﹪
步骤三:数据的描述
条形统计图
人数
节目类别
20
15
10
5
0
新闻 体育 动画 娱乐 戏曲
4
10
15
18
3
图10.1-1 (1)
全班同学最喜爱节目的人数统计图
条形统计图的特点: 条形统计图能清楚
地表示出每个项目
的具体数目。
问题1
讨论2:你能根据表10-1和图10.1-1
说出全班同学喜爱五类电视节目的情况
吗?
讨论3:如何根据百分比或圆心角画出相应的扇形图?
问题1
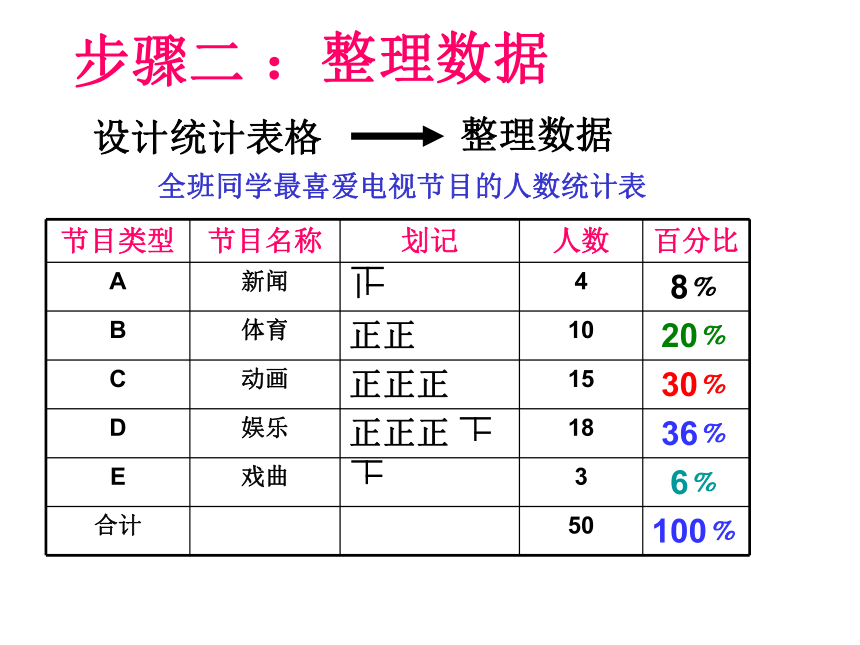
步骤二
设计统计表格
整理数据
节目类型 节目名称 划记 人数 百分比
A 新闻 4 8﹪
B 体育 正正 10 20﹪
C 动画 正正正 15 30﹪
D 娱乐 正正正 18 36﹪
E 戏曲 3 6﹪
合计 50 100﹪
全班同学最喜爱电视节目的人数统计表
:整理数据
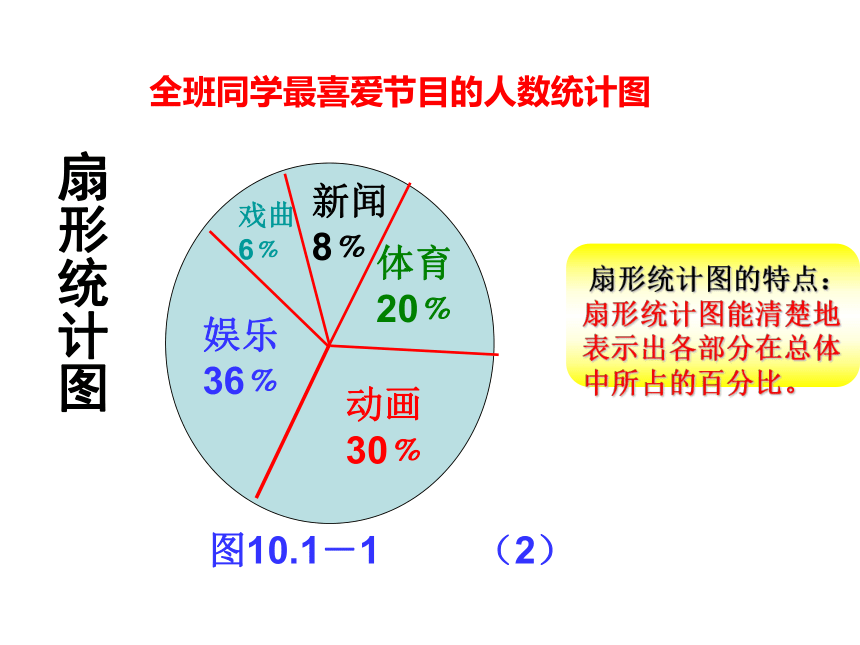
扇形统计图
全班同学最喜爱节目的人数统计图
动画
30﹪
娱乐
36﹪
戏曲
6﹪
新闻8﹪
体育
20﹪
图10.1-1 (2)
扇形统计图的特点: 扇形统计图能清楚地表示出各部分在总体中所占的百分比。
在全班同学中,喜爱娱乐的最多,有18人,占全班人数的36%;喜爱动画的同学人数排在第二位,分别有15人,各占全班人数的30%;喜爱体育的同学人数排在第三位,有10人,占全班人数的20%;喜爱新闻和戏曲的同学人数分别排在第四位和第五位,各有4人和3人,占全班人数的8%和 6%
步骤四:数据分析
假设有一位同学忘了上交调查问卷,
这次调查是全面调查吗?
在这次调查中,全班同学是我们要
考察的全体对象,我们对全体对象进行
了调查,像这样考察全体对象的调查属
于全面调查(也叫普查).
你还能举出生活中全面调查的
实例吗?与同伴交流.
全体对象
下列调查属于全面调查有:( )
D、调查我们班全体同学的体重情况
C、中央电视台2005年春节联欢晚会“您最喜
欢的节目”网上调查
B、乘飞机时,机场对旅客的行李安全检查
A、调查南大附中全体教师某一周内用电情况
A
B
D
如图是某校七年级二班学生最喜欢的球类活动的调查结果,整个圆表示全班的学生数共50人。由图可知:喜欢足球运动的有 人,喜欢篮球运动的有 人。
运动的有 人,喜欢篮球运动的有 人。
运动的有 人,喜欢篮球运动的有 人。
喜欢足球的人数=全班学生数×喜欢足球的人数的百分比,因此,有:
50 ×30%=15
喜欢篮球的人数=全班学生数×喜欢篮球的人数的百分比,因此,有:
50 ×28%=14
15
14
篮球28%
对某班40名同学的一次数学成绩进
行统计, 适当分组后80~90分这个分数段
的划记人数为: 正一 , 那么这个班这个分
数段的人数占全班人数的百分比是( )
A、20% B、40%
C、15% D、25%
C
你会看扇形图吗 某校对七年级200名
学生对“月球上是否有水”进行统计调查,
从图中可以看出,认为“没有”的学生有多
少人 “不知道”的呢?
描述数据
全面调查的基本过程
整理数据
收集数据
(调查问卷)
(统计表格)
(条形图、扇形图)
全面调查
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样.
在抽样调查中,我们把要考察的全体对象称为总体。
组成总体的每一个考察对象称为个体。
被抽取的那些个体组成一个样本。
样本中个体的数目叫样本容量。
样本容量不含单位
问题一:某班有50名学生,想要了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,你会怎么做
问题二:某校有2000名学生,想要了解全校同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,你会怎么做
问题三:某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,我们又该怎么做
(全面调查)
(抽样调查——简单随机抽样)
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题二中对学生的调查数据去估计整个地区电视观众的情况呢?
答:(1)用对学生的调查数据去估计整个地区观众的情况是不合适的.因为学生、成年人、老年人喜欢的电视节目往往有明显的不同,所以要了解整个地区的观众的情况,需要在更大范围内抽取样本.
问题3
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题2中对学生的调查数据去估计整个地区电视观众的情况呢?
(2)如果抽取一个容量为1 000的样本进行调查,你会怎样调查?
答:(2)由于各年龄段对节目爱好有明显的不同,而同一个年龄段对节目的喜爱又存在共性,因此可以对青少年、成年人、老年人各个人群分别独立进行简单随机抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果.
问题3
一、分层抽样的定义: 先将总体分成几个年龄段(层)然后再在各年龄段(层)中进行简单随机抽样 ,我们把这样的抽样方法叫分层抽样。
二、分层抽样的步骤:
⑴分层:将总体按一定标准分层;
⑵计算:按各层个体数的比确定各层应抽取的数量.
⑶抽样:在每一层进行抽样 --简单随机抽样。
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题2中对学生的调查数据去估计整个地区电视观众的情况呢?
(2)如果抽取一个容量为1 000的样本进行调查,你会怎样调查?
(3)若该地区青少年、成年人、老年人的人数比为2:5:3.现抽取一个容量为1 000的样本进行调查,则各需抽取多少名?
方法: 根据各年龄段实际人口的比例,确定青少年、成年人、老年人的人数比为2:5 :3,抽取一个容量为1 000的样本,具体按下表进行抽取:
青少年 成年人 老年人 合计
抽取
人数
1. 这样获取的样本与这个地区所有观众的年龄结构基本相同.
2.因为各年龄段对某一节目喜好程度有明显差别,所以这样抽取样本,与在整个地区直接进行简单随机抽样相比,更具有代表性,能更好地反映总体.
200
500
1000
300
人数
类型 青少年 成年人 老年人 合计 百分比
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
抽样调查1000名观众最喜爱节目的人数统计表
若根据合计这一列,可用哪种统计图描述数据?
根据统计图得出什么结论?
一、同一年龄段对各节目的喜爱情况(纵向比较)
人数
类型 青少年 成年人 老年人 合计 百分
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
二、各年龄段对同一节目的喜爱情况(横向比较)
各个年龄段中观众对动画类节目喜爱情况统计表
年龄段
类型 青少年 成年人 老年人
人数 55 53 18
百分比 27.5% 10.6% 6%
根据这张统计表,可用哪种统计图描述数据?
折线统计图的特点:折线统计图能清楚地反映数据的变化趋势。
人数
类型 青少年 成年人 老年人 合计 百分
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
二、各年龄段对新闻类节目的喜爱情况(横向比较)
各个年龄段中喜爱新闻类节目情况统计表
年龄段
类型 青少年 成年人 老年人
人数 11 125 103
百分比 5.5% 25% 34%
各年龄段喜欢新闻类节目百分比的折线统计图
结论?
由表10-3中的数据,可以估计各个年龄段中观众对动画类节目和娱乐类节目喜爱的百分比比为:
青少年 成年人 老年人
动画 27.5% 10.6% 6%
娱乐 37% 35.2% 19.7%
40﹪
30﹪
20﹪
10﹪
0﹪
青少年 成年人 老年人 年龄段
百分率
娱乐
动画
各年龄段喜欢动画类节目和娱乐类节目
百分比的折线统计图
可以在同一图中作多种折线
如图是某商场销售雨伞的情况:
请观察折线图回答问题:
(1)哪个季度雨伞销售量最大?
(2)请你为这家商场就进货问题提出建议。
折线统计图的特点: 折线统计图能清楚地反映事物的变化情况。
分层抽样的步骤是:
(1)将总体按一定标准分层;
(2)计算各层的个体数与总体的个体数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(4)在每一层进行抽样(可用简单随机抽样)。
类 别 各自特点 相互联系 适用范围 共同点
简单随机抽样 从总体中逐个抽取 总体中的个体个数较少 在抽样过程中每个个体被抽取的概率相等(体现抽样方法的客观性和公平性)
分层抽样 将总体分成几层,按各层个体数之比 各层抽样时采用简单随机抽样 总体由差异明显的几部分组成
两种抽样方法的比较
8、我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,
统计结果如下:
每户丢弃塑料袋的个数 2 3 4 5
户 数 6 30 27 12
根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃______个塑料袋。
(2)这天,丢弃3个塑料袋的家庭户数占总户数的________。
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃
的塑料袋有_________个。
作业:1、为了解某中学初中三年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
175 161 171 176 167 181 161 173 171 177 179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分:
(1)请填写表中未完成的部分。
(2)根据表中数据整理与计算回答:该校初中三年级男学生身高在171.5~176.5(厘米)范围内的人数为多少。
分 组 划记 人数 百分比
156.5~161.5 3 15%
161.5~166.5 丅 2 10%
166.5~171.5 4 20%
171.5~176.5 正- 30%
176.5~181.5 正 5
合 计 20 100%
2、春节文艺晚会是大家都喜欢的节目,下面是路刚班级喜爱某种节目的人数分布表,但因不小心,他打翻墨水,有些地方被墨水遮掉了。请你帮他解决以下问题。
节目编号 节目类别 划计 人数 百分比
1 相声 ① ② ③
2 小品 8 19%
3 歌曲 正 5 12%
4 舞蹈 8 19%
5 杂技 7 17%
6 戏曲 3 7%
合计 42 42 100%
(1)被墨水遮掉的3处应是
① _______ ②_______
③________
(2)从上表中可知
该班同学喜欢_______
的人数最多。
(3)画出条形图表示全班同学喜欢某种节目的分布情况。
2000年10万人中受教育程度分布统计图
例2.
(1)三幅统计图分别表示什么内容?
(2)哪幅统计图你能看出10万人中大学人
数变化情况?
(3)2000年10万人中初中人数是多少?你
是从哪幅图中得到这个数据的?
(4)2000年10万人中初中人数约占多少 吗?
你从哪幅统计图中可以明显得到?
(5)比较三种统计图的特点,并相互交流
答:折线统计图表示了2000年10万人 中各教育程度的变化情况; 扇形统计图表示了10万人中受教 育程度分布情况;条形统计图表示了10万人中各教育程度的人均具体数量。
(1)三幅统计图分别表示什么内容?
(2)哪幅统计图你能看出10万人中大学人 数变化情况?
答:折线统计图
答: 2000年10万人中初中人数是33961,
是从条形统计图中得出的。
(3)2000年10万人中初中人数是多少?你是从哪幅图中得到这个数据的?
答: 2000年10万人中初中人数占34% ,
是从扇形统计图中得到的。
(4)2000年10万人中初中人数约占多少 吗?你从哪幅统计图中可以明显得到?
(5)比较三种统计图的特点,并相互交流
扇形统计图
条形统计图
折线统计图
条形统计图能清楚地表示出每个项目的具体数目。
扇形统计图能清楚地表示出各部分在总体中所占的百分比。
折线统计图能清楚地反映事物的变化情况。
2.
思考:
运动名称 划记 人数 百分比
乒乓球 正正正 16
羽毛球 正正正 15
篮球 正正 10
足球 正 9
合计
下表是王刚对全班同学喜爱某一项球类活动进行的一次全面调查,统计数据如下:
全班同学喜爱某种球类活动的人数分布表
请填表和画出它的条形图。
32%
30%
20%
18%
50
50
100%
人数
16 14 12 10 8 6 4 2 0
乒乓球 羽毛球 篮球 足球 名称
解:
课后练习
1. 统计图可以帮助我们非常直观地发现一些有意义的结结论,我们已经学过三种统计图,分别是____统计图, ___统计图 ___ 统计图.
2.要描述我国连续5年在奥运会上获得金牌总数的变化情况,应选择_______统计图表示。
条形
折线
扇形
折线
3.如图4.1 所示,回答下列问题:
(1)如果整个圆表示总体,那么扇形____代表整体的25%.
(2)如果整个圆代表9公顷稻田,那么扇形C大约代表_____公顷稻田.
A
5.247
例3.制作适当统计图表示下列数据:
(1)2000年平均每人每月消费性支出446元,其中食品占40.6%,衣着12.2%,家庭设备用品及服务7.0%,医疗保健5.9%,交通和通迅8.7%,娱乐教育文化服务12.7%,居住8.6%,杂项商品4.3%。
第一组数据表示的是各部分所占百分比,宜用扇形统计图。
2、某校对七年级800名学生的上学方式
进行调查如图所示:
骑自行车60%
公共汽车
步行28%
则乘公共汽车的人数占总人数的 ,有 人。
96
12%
例4 小李通过某地区1998年至2000年快餐公司发展情况的调查,制成了该地区的快餐公司个数情况的条形图1.1-2①和快餐公司盒饭年销量的平均数情况条形图1.1-2②.利用图1.1-2①、图1.1-2②共同提供的信息解答下列问题.
(1)2000年该地区快餐公司有 个;
(2)1999年平均每个快餐公司盒饭年销
量是 万盒,2000年每个快
餐公司盒饭年销量是 万盒.
(3)2000年该地区快餐公司共销售盒饭
_____万盒.
80
1.5
2
160
10.1统计调查
步骤一:收集数据
设计调查问卷
调查问卷 年 月 日
姓名 在下面五类电视节目中,你最喜爱的是( )(单选)
A新闻 B体育 C动画 D娱乐 E戏曲
填写调查问卷
收集调查问卷
问题1
某同学经调查,得到如下50个数据:
CCADBCADCD
CEABDDBCCC
DBDCDDDCDC
EBBDDCCEBD
ABDDCBCBDD
设计调查问卷
填写调查问卷
收集调查问卷
讨论1:从上面的数据中,你能看出全班同学喜爱各类节目的情况吗?怎样才能很清楚地看出全班同学喜爱各类节目的情况?
问题1
统计中经常用表格整理数据:
步骤二:整理数据
设计统计表格
整理数据
节目类型 节目名称 划记 人数 百分比
A 新闻
B 体育
C 动画
D 娱乐
E 戏曲
合计
全班同学最喜爱电视节目的人数统计表
表头
行
列
注:划记法是用“正”字的每一划(笔画)代表一个数据。
正正
正正正
正正正
4
10
15
18
3
50
8﹪
20﹪
30﹪
36﹪
6﹪
100﹪
步骤三:数据的描述
条形统计图
人数
节目类别
20
15
10
5
0
新闻 体育 动画 娱乐 戏曲
4
10
15
18
3
图10.1-1 (1)
全班同学最喜爱节目的人数统计图
条形统计图的特点: 条形统计图能清楚
地表示出每个项目
的具体数目。
问题1
讨论2:你能根据表10-1和图10.1-1
说出全班同学喜爱五类电视节目的情况
吗?
讨论3:如何根据百分比或圆心角画出相应的扇形图?
问题1
步骤二
设计统计表格
整理数据
节目类型 节目名称 划记 人数 百分比
A 新闻 4 8﹪
B 体育 正正 10 20﹪
C 动画 正正正 15 30﹪
D 娱乐 正正正 18 36﹪
E 戏曲 3 6﹪
合计 50 100﹪
全班同学最喜爱电视节目的人数统计表
:整理数据
扇形统计图
全班同学最喜爱节目的人数统计图
动画
30﹪
娱乐
36﹪
戏曲
6﹪
新闻8﹪
体育
20﹪
图10.1-1 (2)
扇形统计图的特点: 扇形统计图能清楚地表示出各部分在总体中所占的百分比。
在全班同学中,喜爱娱乐的最多,有18人,占全班人数的36%;喜爱动画的同学人数排在第二位,分别有15人,各占全班人数的30%;喜爱体育的同学人数排在第三位,有10人,占全班人数的20%;喜爱新闻和戏曲的同学人数分别排在第四位和第五位,各有4人和3人,占全班人数的8%和 6%
步骤四:数据分析
假设有一位同学忘了上交调查问卷,
这次调查是全面调查吗?
在这次调查中,全班同学是我们要
考察的全体对象,我们对全体对象进行
了调查,像这样考察全体对象的调查属
于全面调查(也叫普查).
你还能举出生活中全面调查的
实例吗?与同伴交流.
全体对象
下列调查属于全面调查有:( )
D、调查我们班全体同学的体重情况
C、中央电视台2005年春节联欢晚会“您最喜
欢的节目”网上调查
B、乘飞机时,机场对旅客的行李安全检查
A、调查南大附中全体教师某一周内用电情况
A
B
D
如图是某校七年级二班学生最喜欢的球类活动的调查结果,整个圆表示全班的学生数共50人。由图可知:喜欢足球运动的有 人,喜欢篮球运动的有 人。
运动的有 人,喜欢篮球运动的有 人。
运动的有 人,喜欢篮球运动的有 人。
喜欢足球的人数=全班学生数×喜欢足球的人数的百分比,因此,有:
50 ×30%=15
喜欢篮球的人数=全班学生数×喜欢篮球的人数的百分比,因此,有:
50 ×28%=14
15
14
篮球28%
对某班40名同学的一次数学成绩进
行统计, 适当分组后80~90分这个分数段
的划记人数为: 正一 , 那么这个班这个分
数段的人数占全班人数的百分比是( )
A、20% B、40%
C、15% D、25%
C
你会看扇形图吗 某校对七年级200名
学生对“月球上是否有水”进行统计调查,
从图中可以看出,认为“没有”的学生有多
少人 “不知道”的呢?
描述数据
全面调查的基本过程
整理数据
收集数据
(调查问卷)
(统计表格)
(条形图、扇形图)
全面调查
抽样调查是一种方法,它只抽取了一部分对象进行调查,然后根据样本数据推断全体对象的情况。
如果在抽取样本的过程中,总体的每一个个体都有相等的机会被抽到,这样的抽样方法就叫简单的随机抽样.
在抽样调查中,我们把要考察的全体对象称为总体。
组成总体的每一个考察对象称为个体。
被抽取的那些个体组成一个样本。
样本中个体的数目叫样本容量。
样本容量不含单位
问题一:某班有50名学生,想要了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,你会怎么做
问题二:某校有2000名学生,想要了解全校同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,你会怎么做
问题三:某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,我们又该怎么做
(全面调查)
(抽样调查——简单随机抽样)
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题二中对学生的调查数据去估计整个地区电视观众的情况呢?
答:(1)用对学生的调查数据去估计整个地区观众的情况是不合适的.因为学生、成年人、老年人喜欢的电视节目往往有明显的不同,所以要了解整个地区的观众的情况,需要在更大范围内抽取样本.
问题3
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题2中对学生的调查数据去估计整个地区电视观众的情况呢?
(2)如果抽取一个容量为1 000的样本进行调查,你会怎样调查?
答:(2)由于各年龄段对节目爱好有明显的不同,而同一个年龄段对节目的喜爱又存在共性,因此可以对青少年、成年人、老年人各个人群分别独立进行简单随机抽样,使每个年龄段都能抽取一定的人数来代表所在的人群,然后汇总调查结果.
问题3
一、分层抽样的定义: 先将总体分成几个年龄段(层)然后再在各年龄段(层)中进行简单随机抽样 ,我们把这样的抽样方法叫分层抽样。
二、分层抽样的步骤:
⑴分层:将总体按一定标准分层;
⑵计算:按各层个体数的比确定各层应抽取的数量.
⑶抽样:在每一层进行抽样 --简单随机抽样。
问题3:
某地区有500万电视观众,要想了解他们对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.
(1)能不能用问题2中对学生的调查数据去估计整个地区电视观众的情况呢?
(2)如果抽取一个容量为1 000的样本进行调查,你会怎样调查?
(3)若该地区青少年、成年人、老年人的人数比为2:5:3.现抽取一个容量为1 000的样本进行调查,则各需抽取多少名?
方法: 根据各年龄段实际人口的比例,确定青少年、成年人、老年人的人数比为2:5 :3,抽取一个容量为1 000的样本,具体按下表进行抽取:
青少年 成年人 老年人 合计
抽取
人数
1. 这样获取的样本与这个地区所有观众的年龄结构基本相同.
2.因为各年龄段对某一节目喜好程度有明显差别,所以这样抽取样本,与在整个地区直接进行简单随机抽样相比,更具有代表性,能更好地反映总体.
200
500
1000
300
人数
类型 青少年 成年人 老年人 合计 百分比
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
抽样调查1000名观众最喜爱节目的人数统计表
若根据合计这一列,可用哪种统计图描述数据?
根据统计图得出什么结论?
一、同一年龄段对各节目的喜爱情况(纵向比较)
人数
类型 青少年 成年人 老年人 合计 百分
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
二、各年龄段对同一节目的喜爱情况(横向比较)
各个年龄段中观众对动画类节目喜爱情况统计表
年龄段
类型 青少年 成年人 老年人
人数 55 53 18
百分比 27.5% 10.6% 6%
根据这张统计表,可用哪种统计图描述数据?
折线统计图的特点:折线统计图能清楚地反映数据的变化趋势。
人数
类型 青少年 成年人 老年人 合计 百分
A新闻 11 125 103 239 23.9%
B体育 47 114 63 224 22.4%
C动画 55 53 18 126 12.6%
D娱乐 74 176 59 309 30.9%
E戏曲 13 32 57 102 10.2%
合计 200 500 300 1000 100%
二、各年龄段对新闻类节目的喜爱情况(横向比较)
各个年龄段中喜爱新闻类节目情况统计表
年龄段
类型 青少年 成年人 老年人
人数 11 125 103
百分比 5.5% 25% 34%
各年龄段喜欢新闻类节目百分比的折线统计图
结论?
由表10-3中的数据,可以估计各个年龄段中观众对动画类节目和娱乐类节目喜爱的百分比比为:
青少年 成年人 老年人
动画 27.5% 10.6% 6%
娱乐 37% 35.2% 19.7%
40﹪
30﹪
20﹪
10﹪
0﹪
青少年 成年人 老年人 年龄段
百分率
娱乐
动画
各年龄段喜欢动画类节目和娱乐类节目
百分比的折线统计图
可以在同一图中作多种折线
如图是某商场销售雨伞的情况:
请观察折线图回答问题:
(1)哪个季度雨伞销售量最大?
(2)请你为这家商场就进货问题提出建议。
折线统计图的特点: 折线统计图能清楚地反映事物的变化情况。
分层抽样的步骤是:
(1)将总体按一定标准分层;
(2)计算各层的个体数与总体的个体数的比;
(3)按各层个体数占总体的个体数的比确定各层应抽取的样本容量;
(4)在每一层进行抽样(可用简单随机抽样)。
类 别 各自特点 相互联系 适用范围 共同点
简单随机抽样 从总体中逐个抽取 总体中的个体个数较少 在抽样过程中每个个体被抽取的概率相等(体现抽样方法的客观性和公平性)
分层抽样 将总体分成几层,按各层个体数之比 各层抽样时采用简单随机抽样 总体由差异明显的几部分组成
两种抽样方法的比较
8、我校50名学生在某一天调查了75户家庭丢弃塑料袋的情况,
统计结果如下:
每户丢弃塑料袋的个数 2 3 4 5
户 数 6 30 27 12
根据上表回答下列问题:
(1)这天,一个家庭一天最多丢弃______个塑料袋。
(2)这天,丢弃3个塑料袋的家庭户数占总户数的________。
(3)该校所在的居民区共有居民0.8万户,则该区一天丢弃
的塑料袋有_________个。
作业:1、为了解某中学初中三年级300名男学生的身体发育情况,从中对20名男学生的身高进行了测量,结果如下:(单位:厘米)
175 161 171 176 167 181 161 173 171 177 179 172 165 157 173 173 166 177 169 181
下表是根据上述数据填写的表格的一部分:
(1)请填写表中未完成的部分。
(2)根据表中数据整理与计算回答:该校初中三年级男学生身高在171.5~176.5(厘米)范围内的人数为多少。
分 组 划记 人数 百分比
156.5~161.5 3 15%
161.5~166.5 丅 2 10%
166.5~171.5 4 20%
171.5~176.5 正- 30%
176.5~181.5 正 5
合 计 20 100%
2、春节文艺晚会是大家都喜欢的节目,下面是路刚班级喜爱某种节目的人数分布表,但因不小心,他打翻墨水,有些地方被墨水遮掉了。请你帮他解决以下问题。
节目编号 节目类别 划计 人数 百分比
1 相声 ① ② ③
2 小品 8 19%
3 歌曲 正 5 12%
4 舞蹈 8 19%
5 杂技 7 17%
6 戏曲 3 7%
合计 42 42 100%
(1)被墨水遮掉的3处应是
① _______ ②_______
③________
(2)从上表中可知
该班同学喜欢_______
的人数最多。
(3)画出条形图表示全班同学喜欢某种节目的分布情况。
2000年10万人中受教育程度分布统计图
例2.
(1)三幅统计图分别表示什么内容?
(2)哪幅统计图你能看出10万人中大学人
数变化情况?
(3)2000年10万人中初中人数是多少?你
是从哪幅图中得到这个数据的?
(4)2000年10万人中初中人数约占多少 吗?
你从哪幅统计图中可以明显得到?
(5)比较三种统计图的特点,并相互交流
答:折线统计图表示了2000年10万人 中各教育程度的变化情况; 扇形统计图表示了10万人中受教 育程度分布情况;条形统计图表示了10万人中各教育程度的人均具体数量。
(1)三幅统计图分别表示什么内容?
(2)哪幅统计图你能看出10万人中大学人 数变化情况?
答:折线统计图
答: 2000年10万人中初中人数是33961,
是从条形统计图中得出的。
(3)2000年10万人中初中人数是多少?你是从哪幅图中得到这个数据的?
答: 2000年10万人中初中人数占34% ,
是从扇形统计图中得到的。
(4)2000年10万人中初中人数约占多少 吗?你从哪幅统计图中可以明显得到?
(5)比较三种统计图的特点,并相互交流
扇形统计图
条形统计图
折线统计图
条形统计图能清楚地表示出每个项目的具体数目。
扇形统计图能清楚地表示出各部分在总体中所占的百分比。
折线统计图能清楚地反映事物的变化情况。
2.
思考:
运动名称 划记 人数 百分比
乒乓球 正正正 16
羽毛球 正正正 15
篮球 正正 10
足球 正 9
合计
下表是王刚对全班同学喜爱某一项球类活动进行的一次全面调查,统计数据如下:
全班同学喜爱某种球类活动的人数分布表
请填表和画出它的条形图。
32%
30%
20%
18%
50
50
100%
人数
16 14 12 10 8 6 4 2 0
乒乓球 羽毛球 篮球 足球 名称
解:
课后练习
1. 统计图可以帮助我们非常直观地发现一些有意义的结结论,我们已经学过三种统计图,分别是____统计图, ___统计图 ___ 统计图.
2.要描述我国连续5年在奥运会上获得金牌总数的变化情况,应选择_______统计图表示。
条形
折线
扇形
折线
3.如图4.1 所示,回答下列问题:
(1)如果整个圆表示总体,那么扇形____代表整体的25%.
(2)如果整个圆代表9公顷稻田,那么扇形C大约代表_____公顷稻田.
A
5.247
例3.制作适当统计图表示下列数据:
(1)2000年平均每人每月消费性支出446元,其中食品占40.6%,衣着12.2%,家庭设备用品及服务7.0%,医疗保健5.9%,交通和通迅8.7%,娱乐教育文化服务12.7%,居住8.6%,杂项商品4.3%。
第一组数据表示的是各部分所占百分比,宜用扇形统计图。
2、某校对七年级800名学生的上学方式
进行调查如图所示:
骑自行车60%
公共汽车
步行28%
则乘公共汽车的人数占总人数的 ,有 人。
96
12%
例4 小李通过某地区1998年至2000年快餐公司发展情况的调查,制成了该地区的快餐公司个数情况的条形图1.1-2①和快餐公司盒饭年销量的平均数情况条形图1.1-2②.利用图1.1-2①、图1.1-2②共同提供的信息解答下列问题.
(1)2000年该地区快餐公司有 个;
(2)1999年平均每个快餐公司盒饭年销
量是 万盒,2000年每个快
餐公司盒饭年销量是 万盒.
(3)2000年该地区快餐公司共销售盒饭
_____万盒.
80
1.5
2
160
