18.2特殊的平行四边形学案(5课时,无答案)
文档属性
| 名称 | 18.2特殊的平行四边形学案(5课时,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 109.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 22:00:17 | ||
图片预览




文档简介
课题:18.2.1矩形1 班级: 姓名:
学习目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.???
2.会初步运用矩形的概念和性质来解决有关问题.???
学习重点、难点:
1.重点:矩形的性质.2.难点:矩形的性质的灵活应用.
环节一、先学后议:
1.矩形定义:有一个角是 的平行四边形叫做矩形(通常也叫长方形).
2.【探究矩形的性质】
⑴矩形性质1 矩形的四个角都是 .
⑵矩形性质2 矩形的对角线 .
⑶证明矩形性质2
已知,四边形ABCD是矩形,求证:AC=BD
如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=AC=BD.因此可以得到直角三角形的一个性质:直角三角形斜边上的中线等于 .
⑷证明这个性质:
已知,Rt△ABC中,∠C=90°,CD是斜边AB上的中线,求证:CD=AB
环节二、例题精练:
例1 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
练习:如图 ,矩形 ABCD,AB长8 cm ,对角线BD比AD边长4 cm.求AD的长及点A到BD的距离AE的长.
环节三、随堂练习:
1. 已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的锐角的度数为 .(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的宽为 cm,长为 cm.
2.(选择)(1)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
(A)2对 (B)4对 (C)6对 (D)8对
3.如图,矩形ABCD中,AB=2BC,且AB=AE,求∠CBE的度数.
课题:18.2.1矩形 2 班级: 姓名:
学习目标:
1.理解并掌握矩形的判定方法;
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
学习重点、难点:
1.重点:矩形的判定;2.难点:矩形的判定及性质的综合应用.
学习过程:
(一)复习、预习
1.⑴平行四边形的定义: ;
⑵矩形的定义: ;
2.矩形的特殊性质:⑴ ;⑵ ;
3.【探究矩形的判定方法】
⑴问题:我们知道,课桌的桌面都应该是矩形,小明特别想知道自己课桌的桌面是否为矩形,你能帮他设计测量的方法检验判断课桌面是否为矩形吗?
⑵ 猜测:
矩形判定方法1: 是矩形.
矩形判定方法2: 是矩形.
⑶证明:
已知: 。
求证:
练习: 下列各句判定矩形的说法是否正确?为什么?
??? (1)有一个角是直角的四边形是矩形; ( )
??? (2)有三个角是直角的四边形是矩形; ( )
??? (3)四个角都相等的四边形是矩形; ( )
?????(4)对角线相等的四边形是矩形; ( )
?????(5)对角线相等且互相垂直的四边形是矩形; ( )
(6)对角线互相平分且相等的四边形是矩形; ( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
??? (9)两组对边分别平行,且对角线相等的四边形是矩形. ( )
二、例题与练习
例1: 已知 □ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,
⑴求证:□ABCD是矩形;⑵求这个平行四边形的面积.
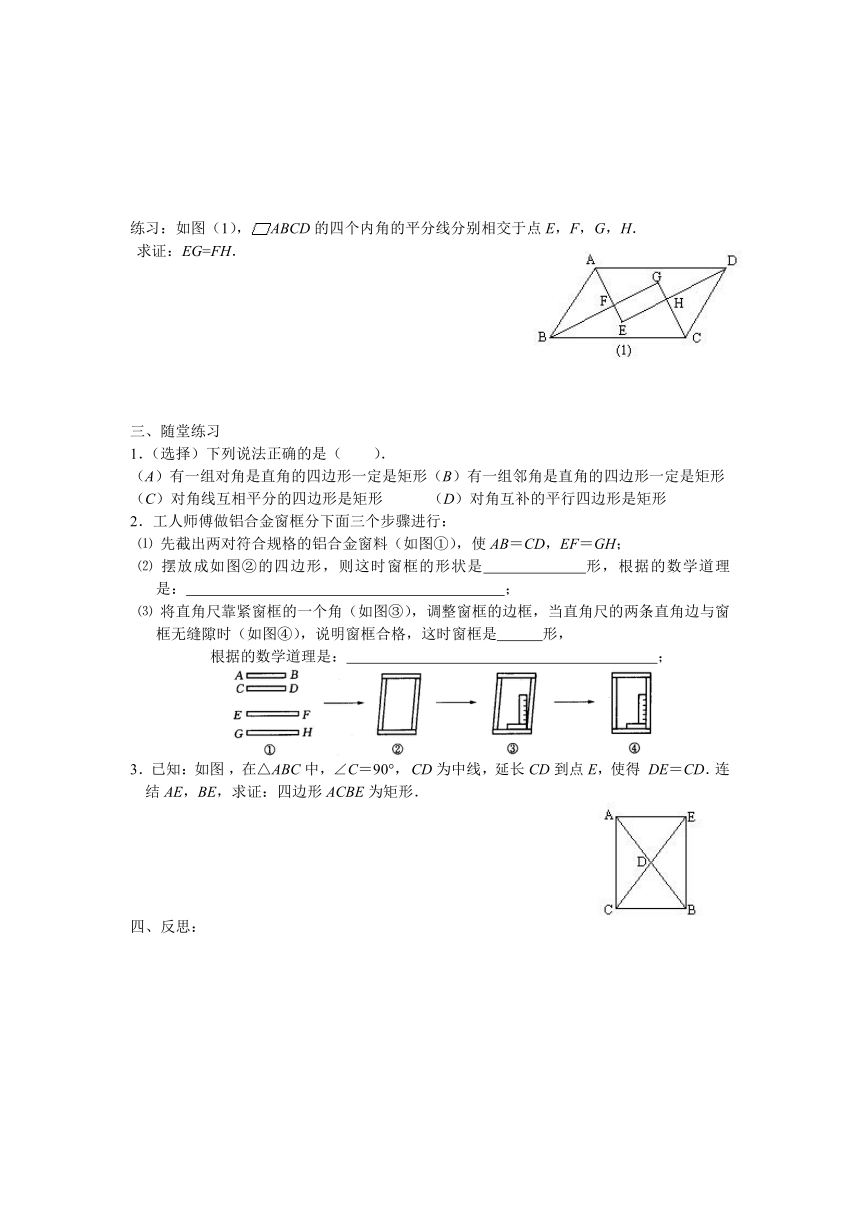
练习:如图(1),ABCD的四个内角的平分线分别相交于点E,F,G,H.
求证:EG=FH.
三、随堂练习
1.(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形 (D)对角互补的平行四边形是矩形
2.工人师傅做铝合金窗框分下面三个步骤进行:
⑴ 先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
⑵ 摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: ;
⑶ 将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是 形,
根据的数学道理是: ;
3.已知:如图?,在△ABC中,∠C=90°,?CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,求证:四边形ACBE为矩形.
四、反思:
课题:18.2.2菱形 1 班级: 姓名:
学习目标:
1.理解菱形的定义;
2.掌握菱形的性质。
学习重点、难点:
1.重点:菱形的性质.2.难点:菱形的性质的灵活应用.
学习过程:
一、复习引入新知
(一).复习
1. 的四边形叫平行四边形。
2. 的平行四边形叫矩形。
(二).新知导学
1.有一组_____ _ ___相等的平行四边形叫菱形。
平移平行四边形的一条边,使它与相邻的一条边_________就能得到一个菱形。
2.菱形的性质:
菱形是特殊的 ,它具有 的一切性质。
如图,菱形ABCD的对角线AC与BD相交于点O,请你回答下列问题,并说明理由。
图中的那些线段相等?那些角相等?
_________________________ _____
②AC与BD有什么特殊的位置关系?
_____________________ ________
经历上述问题的思考与解决你可以发现菱形具有的特殊(一般平行四边形没有的)性质:
①菱形的四条边____________________
②菱形的两条对角线_____________,并且每一条对角线平分______________.
二、例题与练习
1.在菱形ABCD中,对角线AC、BD的长分别为a、b,AC、BD相交于点O
(1)用含有a、b的代数式表示菱形ABCD的面积S;
(2)若a=3cm,b=4cm,求菱形ABCD的面积和周长
2.菱形ABCD的周长为20cm,相邻两角的度数的比为1﹕2,求对角线的长
回顾与反思:菱形的面积等于它两条对角线长的积的__________
三、随堂练习
1.菱形是轴对称图形,对称轴是_________,又是中心对称图形,对称中心是____
2.菱形的两条对角线把菱形分成_____个全等的_______三角形.
3.菱形的两对角线长分别为10cm和24cm,则周长为_________cm,面积为 c㎡。
4.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
5.菱形ABCD中,∠D∶∠A=3∶1,菱形的周长为 8cm,则菱形的高是 .
6.菱形具有而平行四边形不一定具有的性质是___________________(填代号)
①对边平行且相等; ②4条边都相等; ③对角线互相垂直;
④对角相等 ⑤对角线相等; ⑥中心对称图形;
⑦轴对称图形; ⑧每一条对角线平分一组对角
7.菱形具有而矩形不一定具有的特征是( )
A对角线相等; B四个内角都相等;
C对角线互相平分 ; D对角线互相垂直。
8.如图,菱形ABCD中,AC=6cm,BD=8cm求菱形ABCD的周长和面积
9.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.
求证:∠AEF=∠AFE.
四、反思:
课题:18.2.2菱形2 班级: 姓名:
学习目标:
1.理解菱形的判定;
2.会证明四边形是菱形。
学习重点、难点:
重点:菱形的判定.2.难点:菱形的性质与判定的综合应用.
学习过程:
一、复习引入新知
(一)、复习
1、有一组_____ _ ___相等的平行四边形叫菱形。
2、菱形是特殊的平行四边形,它具有平行四边形一切性质,还具有特殊性质。
其特殊性质有:①四边___ __________,
②对角线互相________,且每一条对角线平分_______________.
(二)、新知导学
1、在平行四边形ABCD中,AC⊥BD,垂足为O,平行四边形是菱形吗?为什么?
经历上述问题的思考、解答,你可以发现判定菱形的方法:
判定1:对角线 的平行四边形是菱形。
2、画菱形的方法:先画两条等长的线段AB、AD,然后分别以B、D为圆心,以AB为半径画弧,得到两弧交于点C,连接BC、DC,就画出了一个_________。(按上述操作画出图形)
判定2:四边相等的____________是菱形。
归纳:菱形常用的判定方法为:
二、例题与练习
1、在平行四边形ABCD中,对角线AC的垂直平分线与边AD、BC分别相交于点E、F,
四边形AFCE是菱形吗?说说你的理由.
练习、矩形ABCD的对角线相交于点O,DE//AC,AE//DB,AE、DE交于点E,
请问:四边形DOAE是什么四边形?请说明理由
三、随堂练习 1、下列说法中,正确的有( )
①一组邻边相等的四边形是菱形.
②对角线互相垂直且有一组邻边相等的四边形是菱形.
③对角线互相平分且有一组邻边相等的四边形是菱形.
④一组邻边相等且有一条对角线平分一组对角的四边形是菱形.
⑤四条边都相等的四边形是菱形.
A、1个 B、2个 C、3个 D、 4个
2、如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD就是菱形;
3、如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,EF∥AB交BC于F,试问:图中的四边形ABFE和四边形EFCD都是菱形吗?请说明理由。
4、如图,△ABC中,AB=AC,AD是角平分线,E为AD延长线上一点,CF//BE交AD于F,连接BF、CE,求证:四边形BECF是菱形。
四、反思
课题:18.2.3正方形 班级: 姓名:
学习目标:
1、理解正方形的定义;
2、掌握正方形的性质和判定。会用正方形的性质解决问题;
3、理解正方形与矩形,菱形区别与联系。
学习过程:
一.新知导学
1.(1)有一组邻边 且有一个角是 的平行四边形叫做正方形
(2)正方形既是特殊的矩形,又是特殊的菱形,因而正方形具有矩形、菱形的一切性质,请写出正方形的所有性质:
边 角 对角线 对称性
正 方 形 的 性 质
2.正方形的判定
(1)有一组邻边 的矩形是正方形。
(2)有一个角是 的菱形是正方形。
(3)有一组邻边 且有一个角是 的平行四边形叫做正方形
(4)对角线____________________的平行四边形是正方形.
二、例题与练习
1.把如图的正方形剪成四个全等的直角三角形。
请用这4个全等的直角三角形拼成符合下列要求的图形
(全部用上,互不重叠且不留空隙),把你的拼法按照实际大小画出。
(1)不是正方形的菱形;
(2)不是正方形的矩形;
(3)既不是矩形也不是菱形的平行四边形
2.如图,四边形ABCD和四边形CEFG都是正方形,试探索BG与DE的关系。
三、随堂练习
1.(1)正方形的边长为2,则对角线长为 。
(2)正方形的边长与对角线长之比为 。
(3)正方形的对角线长为a,则正方形的面积为 。
2.正方形具有而菱形不一定具有的特征是( )
A对角线互相垂直; B对角线互相平分 ; C对角线相等 ; D四条边都相等。
3.正方形具备而矩形不一定具备的性质是 ( )
A.四个角都是直角 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
4.矩形、菱形、正方形都具有的性质是( )
A对角线相等 B对角线互相平分
C对角线平分一组对角 D对角线互相垂直
5.已知:如图,四边形ABCD是正方形,对角线AC、BD交于点O。
求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形。
6.已知:如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且DE=BF.
求证:EA⊥AF.
四、反思
D
C
B
A
D
C
B
A
O
D
C
B
A
A
D
C
B
O
C
A
D
B
C
A
E
D
F
B
F
B
D
A
C
G
E
A
O
D
C
B
