北师大版七年级数学下册 第四章 三角形中角度计算相关的模型 讲义含答案
文档属性
| 名称 | 北师大版七年级数学下册 第四章 三角形中角度计算相关的模型 讲义含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 22:35:35 | ||
图片预览

文档简介
三角形中与角度计算相关的模型
两个定理:
1、平面内,三角形的三个内角和为180°。
2、平面内,三角形的一个外角等于其不相邻的两个外角和。
由上述两个定理可导出本文如下说要讲述的相关模型:8字模型、飞镖模型、两内角角平分线模型、两外角角平分线模型、内外角角平分线模型、共顶点的角平分线与高线夹角模型。下面一一推导证明。
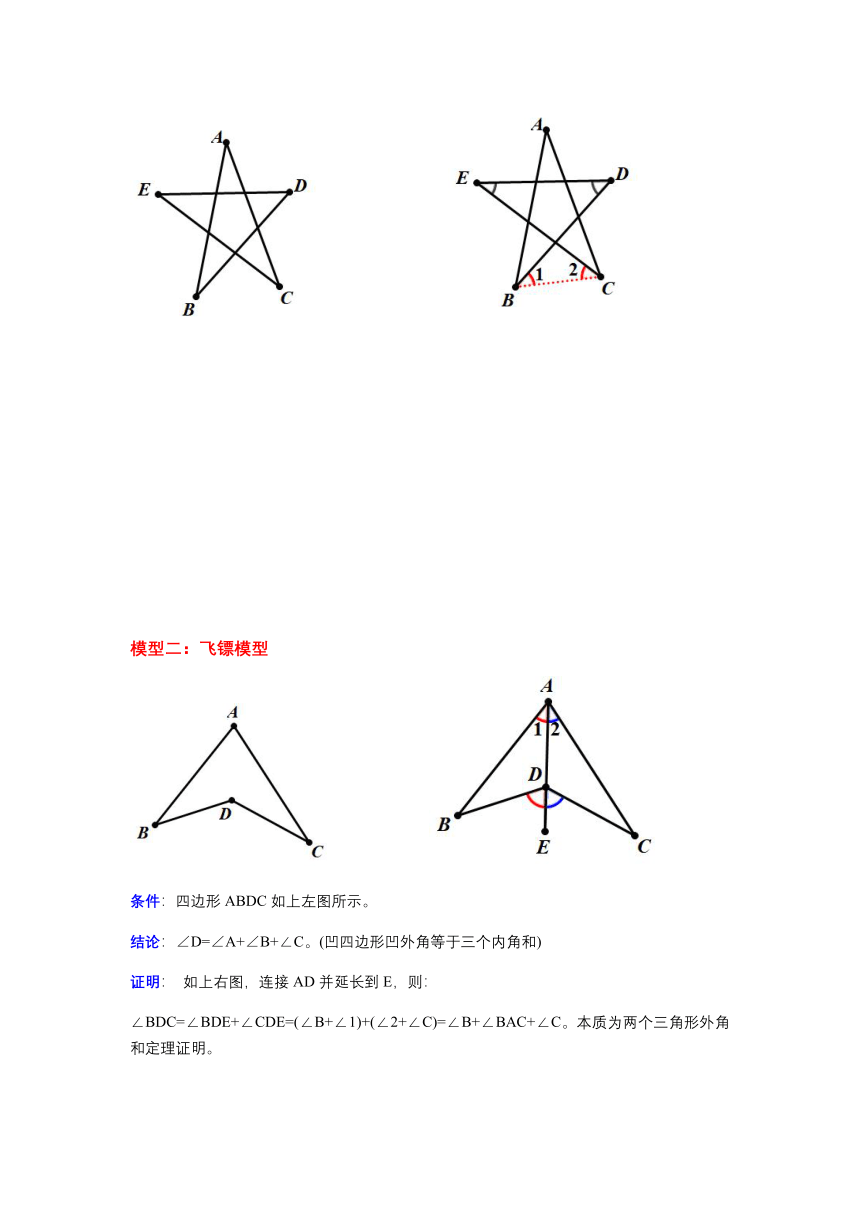
模型一:8字模型
条件:AD、BC相交于点O。
结论:∠A+∠B=∠C+∠D。(上面两角之和等于下面两角之和)
证明: 在△ABO中,由内角和定理:∠A+∠B+∠BOA=180°
在△CDO中,∠C+∠D+∠COD=180°,
∴∠A+∠B+∠BOA=180°=∠C+∠D+∠COD,
由对顶角相等:∠BOA=∠COD
故有∠A+∠B=∠C+∠D
应用:如下左图所示,五角星中,∠A+∠B+∠C+∠D+∠E=180°
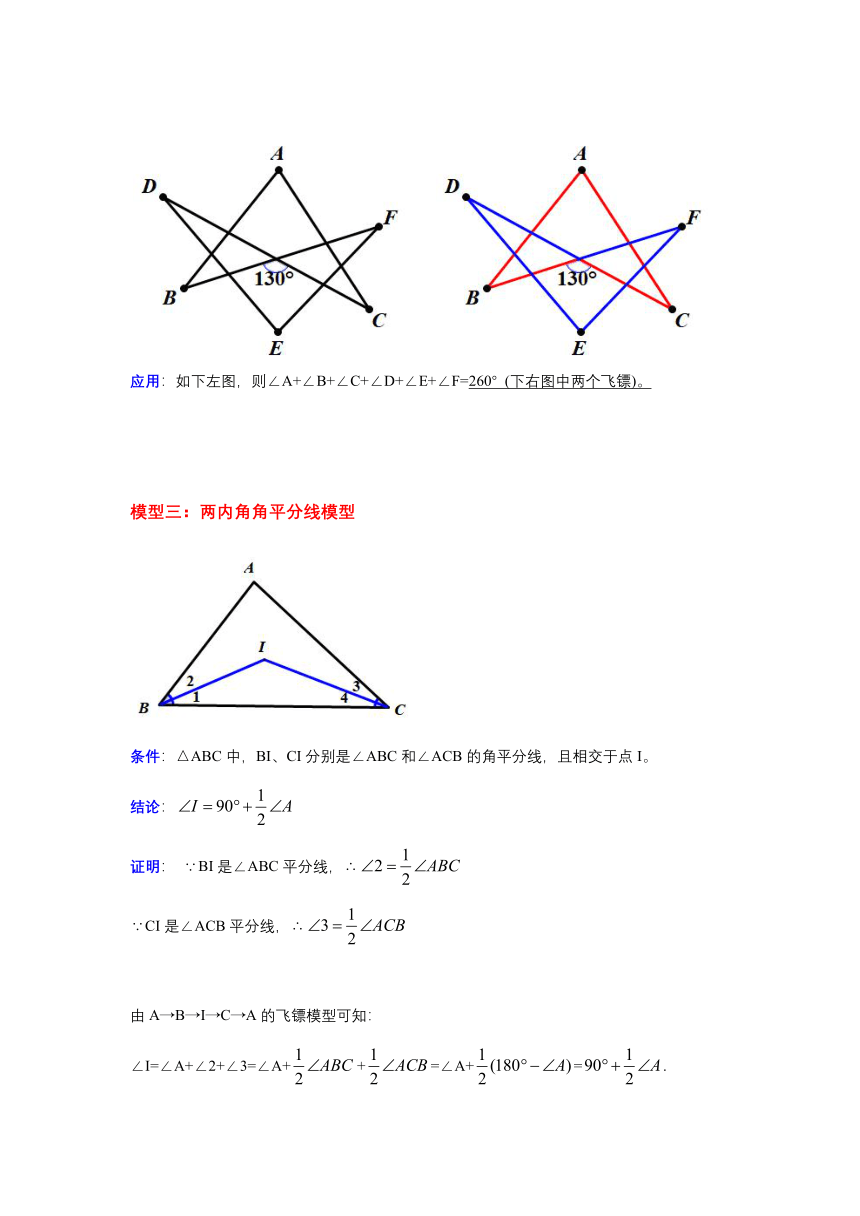
模型二:飞镖模型
条件:四边形ABDC如上左图所示。
结论:∠D=∠A+∠B+∠C。(凹四边形凹外角等于三个内角和)
证明: 如上右图,连接AD并延长到E,则:
∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C。本质为两个三角形外角和定理证明。
应用:如下左图,则∠A+∠B+∠C+∠D+∠E+∠F=260° (下右图中两个飞镖)。
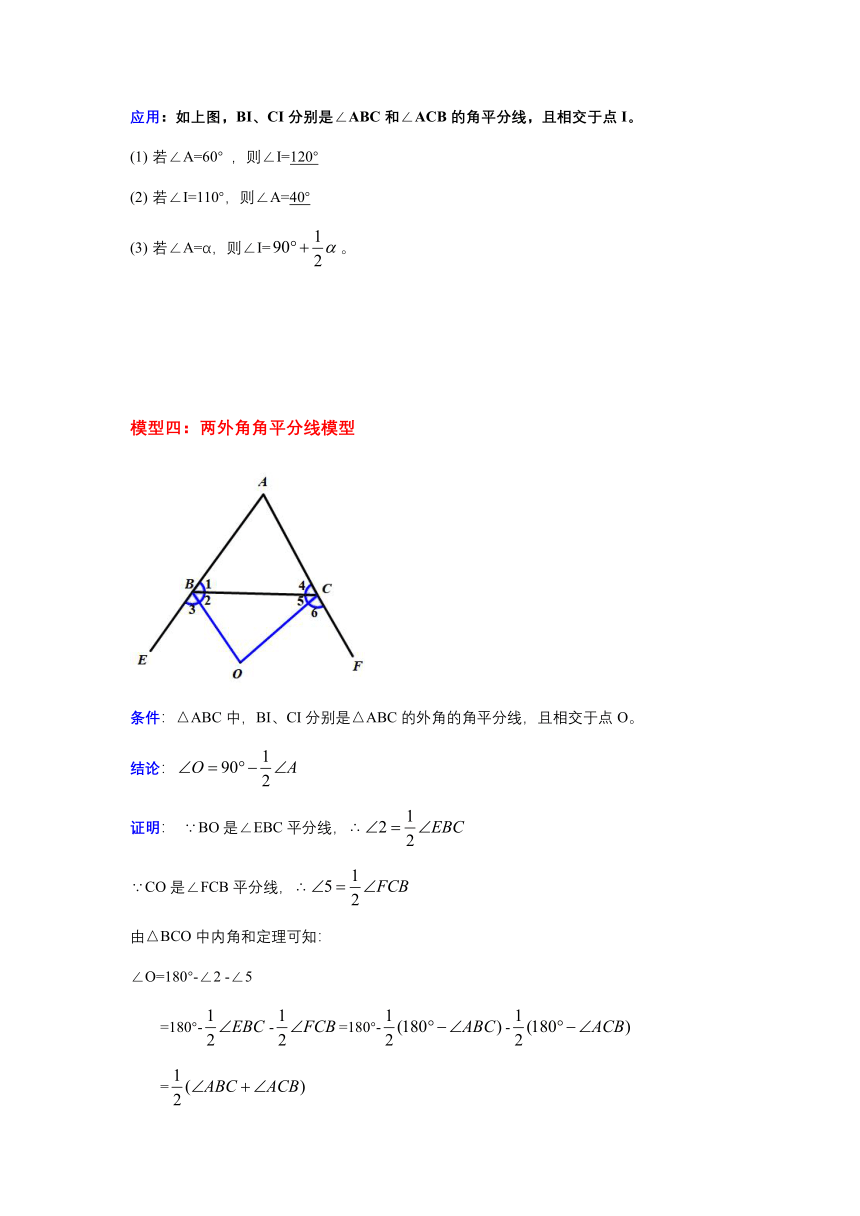
模型三:两内角角平分线模型
条件:△ABC中,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I。
结论:
证明: ∵BI是∠ABC平分线,∴
∵CI是∠ACB平分线,∴
由A→B→I→C→A的飞镖模型可知:
∠I=∠A+∠2+∠3=∠A++=∠A+=.
应用:如上图,BI、CI分别是∠ABC和∠ACB的角平分线,且相交于点I。
(1) 若∠A=60° ,则∠I=120°
(2) 若∠I=110°,则∠A=40°
(3) 若∠A=α,则∠I=。
模型四:两外角角平分线模型
条件:△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O。
结论:
证明: ∵BO是∠EBC平分线,∴
∵CO是∠FCB平分线,∴
由△BCO中内角和定理可知:
∠O=180°-∠2 -∠5
=180°--=180°--
=
=
=
应用:如上图,BO、CO分别是∠ABC和∠ACB的外角角平分线,且相交于点O。
(1)若∠A=60° ,则∠O=60°
(2)若∠O=70°,则∠A=40°
(3)若∠A=α,则∠O=。
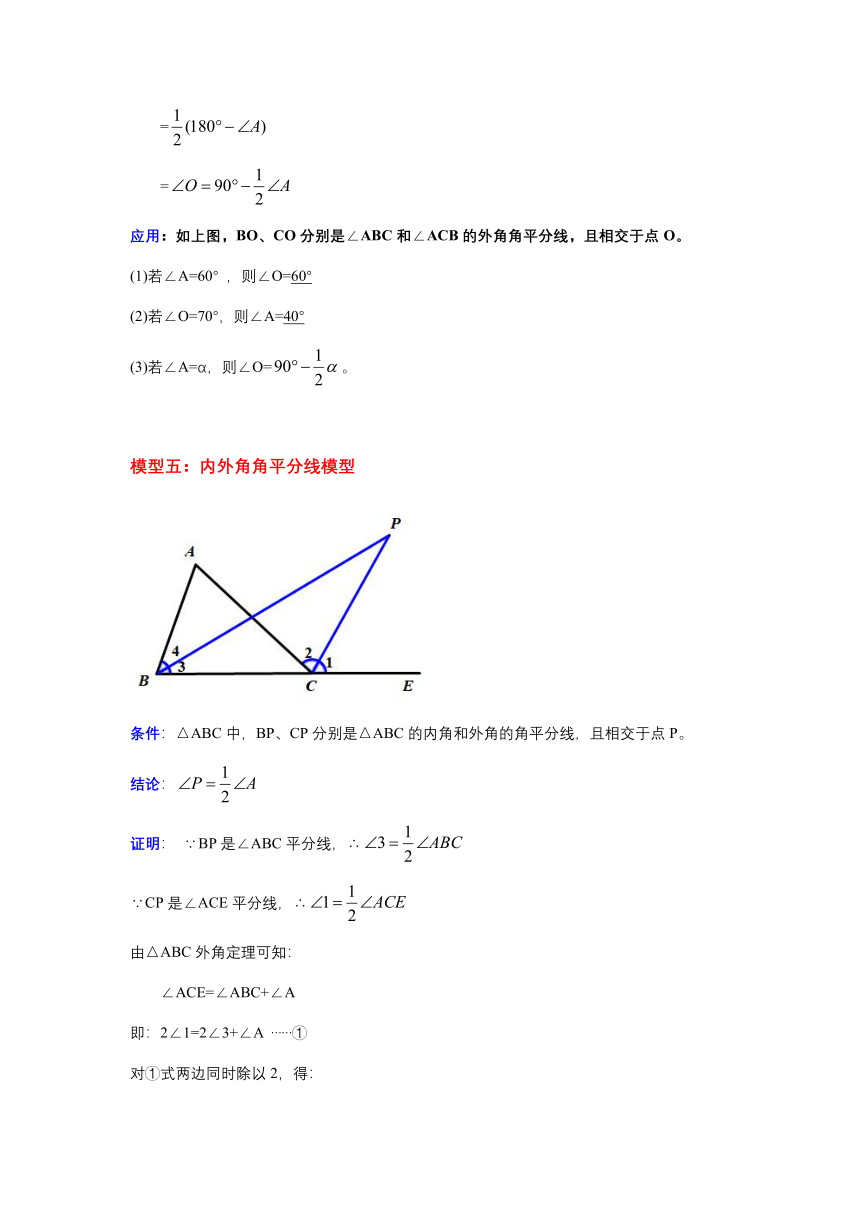
模型五:内外角角平分线模型
条件:△ABC中,BP、CP分别是△ABC的内角和外角的角平分线,且相交于点P。
结论:
证明: ∵BP是∠ABC平分线,∴
∵CP是∠ACE平分线,∴
由△ABC外角定理可知:
∠ACE=∠ABC+∠A
即:2∠1=2∠3+∠A ……①
对①式两边同时除以2,得:
∠1=∠3+ ……②
又在△BPC中由外角定理可知:
∠1=∠3+∠P ……③
比较②③式子可知:
。
应用:如上图,BP、CP分别是∠ABC和∠ACB的外角角平分线,且相交于点P。
(1)若∠A=60° ,则∠O=30°
(2)若∠O=70°,则∠A=140°
(3)若∠A=α,则∠O=
模型六:共顶点角平分线与高线夹角模型
条件:△ABC中,AH是高、AD是∠BAC的角平分线。
结论: (共顶点的高线与角平分线夹角等于两底角之差的一半)
证明: ∵AD是∠ABC平分线,∴
在△AHD中:
∠HAD=90°-∠1=90°-(∠C+∠DAC)
=90°-(∠C+)
=90° - [∠C+]
=
应用:如上图,△ABC中,AH是高、AD是∠BAC的角平分线。
(1) 若∠C=30°,∠B=60°,则∠HAD=15°。
(2) 若∠HAD=15°,∠C=25°,则∠B=55°。
(3) 若∠B=α,∠C=β,则∠HAD=。
三角形中角度模型汇总
名称 图形 结论
八 字模 型 ∠A+∠B=∠C+∠D
飞 镖模 型 ∠D=∠A+∠B+∠C
两内角角平分线模型
两外角角平分线模型
内外角角平分线模型
共顶点角平分线和中线模型
【课后演练】
1、如下图,∠A=30°,∠B=45°,∠C=50°,则∠D=______°
2、如图,∠B=45°,∠A=30°,∠C=25°,则∠ADC=______°
3、如图,∠A+∠B+∠C+∠D=______°
4、如图,△ABC的内角角平分线相交于点O,若∠O=110° ,则∠A=_____°
5、如图,△ABC的内角角平分线交于点P,△ABC的外角角平分线交于点Q,∠P=130°,则∠A=_____°,∠Q=_____°。
6、在△ABC中,∠A=n°,∠ABC和∠ACD的平分线交于A1,得∠A1=_____°,∠A1BC和∠A1CD的角平分线交于A2,得A2=_____°,∠A2020BC和∠A2020CD的角平分线交于A2021,则∠A2020=________°
7、已知△ABC中,∠A=30°
(1) 如图,∠ABC、∠ACB角平分线交于O,则∠BOC=_______;
(2) 如图,∠ABC、∠ACB三等分线交于点O1和O2,∠BO2C=________;
(3) 如图,∠ABC、∠ACB的n等分线交于点O1、O2....、On-1,请求出∠BOn-1C的度数(用n的代数式表示)
【答案】
1、25°
2、100°
3、230°
4、40°
5、80°、50°
6、、、
7、(1)105°
(2)80°
(3)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
