北师大版高中数学选修2-3第一章第4节《简单计数问题-分配选派问题》课件(共17张PPT)
文档属性
| 名称 | 北师大版高中数学选修2-3第一章第4节《简单计数问题-分配选派问题》课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 15:46:36 | ||
图片预览






文档简介
(共17张PPT)
§4.1简单计数问题--分配问题
北师大版高中数学选修2-3第一章
复习回顾一 排列、组合的基础原理
分类计数原理(加法原理)与分步计数原理(乘法原理)是排列组合的基础原理,是排列组合知识的奠基石。
N=m1+m2+m3+…+mn N=m1.m2.m3.….mn
区别:这些m1,m2,…,mn中的每一个都把任务完成了没?
↑团结协作、众志成城!
↑每一个都光荣地完成啦!
在解决复杂的排列组合问题时常常以这两个原理为出发点,甚至两个原理需要交叉使用,往往“开笔”就需分类或分步!
分组分配问题
(1)合理分类、准确分步的策略,灵活运用位置分析法或元素
分析法;
(2)特殊元素、特殊位置优先法简称“特优法”
(3)正难则反、等价转化的策略;
(4)平均分成问题,用除法去掉分组过程中产生的顺序,
平均分成n组除以“n!”,不均分不必用除法;
复习回顾二 排列、组合部分方法公式
如两个不同的小球分成两组就是1种分法,
用公式推导:
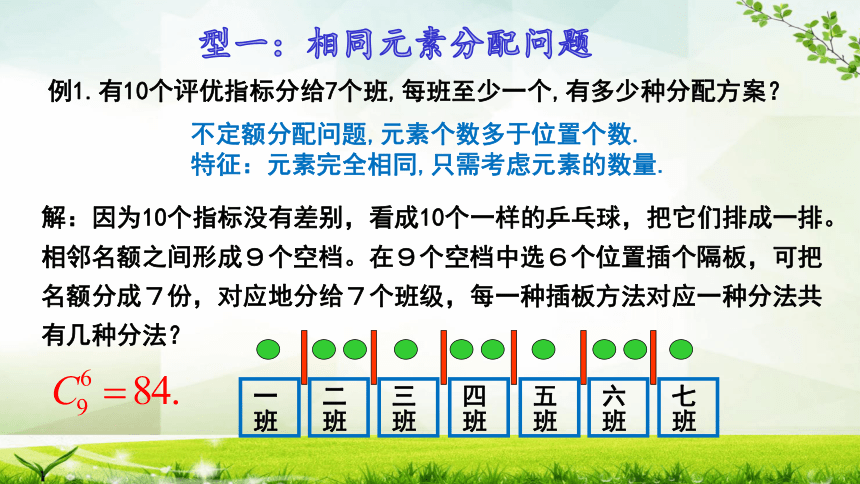
例1.有10个评优指标分给7个班,每班至少一个,有多少种分配方案?
解:因为10个指标没有差别,看成10个一样的乒乓球,把它们排成一排。相邻名额之间形成9个空档。在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有几种分法?
一班
二班
三班
四班
五班
六班
七班
型一:相同元素分配问题
不定额分配问题,元素个数多于位置个数.
特征:元素完全相同,只需考虑元素的数量.
如:将10个相同的球放入5个不同的盒中,每盒至少一个,有多少放法?
结论1:相同元素分配问题---隔板策略
隔板法:将n个相同的元素分成m份,每份至少一个元素,可以将n个
元素排成一排,形成n-1个空隙。将m-1块隔板插入n-1个空
隙中即得m份。分配方法数:
注:隔板法使用条件有两个:(1)元素相同;
(2)每份至少一个元素(人人有份).
例2.求方程 x+y+z+w=100 的正整数解的组数.
隔板法应用之n元一次方程整数解组数问题
变式1.求方程 x+y+z+w=100 的非负整数解的组数.
分析:将每个未知数加1,令X=x+1,Y=y+1,Z=z+1,W=w+1.
方程 X+Y+Z+W=104 的正整数解的组数即为所求.
方法总结:换元法,使得每一个新元为正整数(人人有份).
方法:换元法,使得每一个新元为正整数(每份至少一个元素).
解: x+y+z+w=10变形为:(x-1)+(y-2)+(z+3)+(w+4)=14
令X=x-1,Y=y-2,Z=z+3,W=w+4,即求方程 X+Y+Z+W=14 的正整数解的组数.
隔板法应用之n元一次方程整数解组数问题
变式2.求方程 x+y+z+w=10 的整数解的组数,其中x,y,z,w分
别满足条件:x≥2,y≥3,z≥-2,w>-4.
结论:通过换元法将整数解问题化归为正整数解问题.
例1. 设有6个不同颜色的球,放入3个不同的盒子中,要求每个盒子中至少有一个球,则不同的放法有几种?
1 | 23 | 456 与 1 | 32 | 456 属同一种情况!
结论:不同元素分配问题不能使用隔板法!
型二:不同元素分配问题
X
X
例2、有4本不同的书,若全部借给3个人,每人至少1本,则不同
的借法共有( )种.
B
A错的隐秘!表示首先从4本中选3本分别给3个人,多余的一本随便发.
得两本书的那人重复计数了----误人子弟的“保底法”.
甲 乙 丙
a b cd
a b dc
丙的两本书是分先后发放的(有顺序),导致重复。解决问题的策略:先分成三组(2+1+1)再一次性分配,如答案B.
型二:不同元素分配问题
例3 有6本不同的书,分给甲、乙、丙三个人.(1)如果每人得2本,有多少种不同的分法?(2)如果其中一个人得1本,一个人得2本,一个人得3本,有多少种不同的分法?
两问区别:(1)定额定向分配,均分,(2)定额不定向分配,不均分.
法二:位置分析法(6本书即6个元素,3个人即3个位置):甲,乙,丙
结论2:不同元素分配问题通法--先分组(或堆)再分配
解:
具体分配模式有三种:①1+1+4 ②1+2+3 ③2+2+2
①1+1+4 不完全平均分
②1+2+3 不均分
③2+2+2 平均分(定额定向)
分析:不定额分配问题分类讨论化归为定额分配问题.
总分配方法数N=360+90+90=540.
结论2:不同元素分配问题通法:先分组(或堆)再分配
其中对于定额定向型分配问题也可以采用位置分析法!
回到例1. 设有6个不同颜色的球,放入3个不同的盒子中,
要求每个盒子中至少有一个球,则不同的放法有几种?
1、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加
三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法____种.
分析 分两步考虑, 先选人再分配(先选后排策略).
第一步 按要求取4人;
第二步 将4人分配到三项竞赛活动,分配模式:1+1+2.
不同参赛方法数N=30×36=1080.
法二、定额不定向分配,只能用先分组再分配方法.
随堂演练
2、现有3名医生和6名护士需分配到3所学校为学生体检,每校去1名医生和2名护士,不同的分配方法共有多少种?
随堂演练
法一、分两步:先分组再分配.
1°分组: 将3名医生6名护士9人按要求分成三组
首先6名护士平均分成三组再对应到三个医生(看成三个位
置)方法数:
2°分配: 将三个医护组分配到三所学校:
法二、定额定向分配,可以采用位置分析法.
例1、将4名大学生分配到A,B,C三个不同的学校实习,每个学校至
少分配一人,若甲要求不到A学校,则不同的分配方案共有 种.
型三:有限制条件的分组分配问题
A校 B校 C校
4人:甲,乙,丙,丁
分配模式:1+1+2,按甲属1人组还是2人组讨论:
甲 O OO 或 甲O O O
有限制条件的分组问题,特殊元素优先考虑 (特优法).
例2、有10名学生需分成3组,其中一组4人, 另两组3人但甲、乙不能分在同一组,有多少种不同的分组方法?
分析 10人:甲乙、 OOOOOOOO(8人)
有限制条件的分组问题,特殊元素优先考虑 (特优法).
分组模式:4+3+3. 甲乙是特殊元素,4人组是特殊位置.
分两类:①两人中一人在4人组:甲OOO,乙OO,OOO
②两人均不在4人组:OOOO,甲OO,乙OO
型三:有限制条件的分组分配问题
因为3组有区别,所以可以看成3个盒子,属于分配问题且为定额定向分配,采用位置分析法分步处理更方便!
例3、今有个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有 种.
型三:有限制条件的分组分配问题
车1 车2 车3
4大人2小孩:OOOO oo
①随意搭配
②O OO Ooo 或 O Oo OOo
③OO Oo Oo
分配模式:①3+3; ②1+2+3; ③2+2+2.
方法数为:60+216+72=348.
再见
课堂小结
1、相同元素分配问题,隔板法
2、不同元素分配问题,当元素个数多于位置个数时,总的原则是先分组再分配,属于定额定向分配问题时可采用位置分析法,根据分步计数原理,逐个逐个位置考虑。
3、含特殊元素或特殊位置情形,需要结合特优法---特殊情况优先考虑。
§4.1简单计数问题--分配问题
北师大版高中数学选修2-3第一章
复习回顾一 排列、组合的基础原理
分类计数原理(加法原理)与分步计数原理(乘法原理)是排列组合的基础原理,是排列组合知识的奠基石。
N=m1+m2+m3+…+mn N=m1.m2.m3.….mn
区别:这些m1,m2,…,mn中的每一个都把任务完成了没?
↑团结协作、众志成城!
↑每一个都光荣地完成啦!
在解决复杂的排列组合问题时常常以这两个原理为出发点,甚至两个原理需要交叉使用,往往“开笔”就需分类或分步!
分组分配问题
(1)合理分类、准确分步的策略,灵活运用位置分析法或元素
分析法;
(2)特殊元素、特殊位置优先法简称“特优法”
(3)正难则反、等价转化的策略;
(4)平均分成问题,用除法去掉分组过程中产生的顺序,
平均分成n组除以“n!”,不均分不必用除法;
复习回顾二 排列、组合部分方法公式
如两个不同的小球分成两组就是1种分法,
用公式推导:
例1.有10个评优指标分给7个班,每班至少一个,有多少种分配方案?
解:因为10个指标没有差别,看成10个一样的乒乓球,把它们排成一排。相邻名额之间形成9个空档。在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有几种分法?
一班
二班
三班
四班
五班
六班
七班
型一:相同元素分配问题
不定额分配问题,元素个数多于位置个数.
特征:元素完全相同,只需考虑元素的数量.
如:将10个相同的球放入5个不同的盒中,每盒至少一个,有多少放法?
结论1:相同元素分配问题---隔板策略
隔板法:将n个相同的元素分成m份,每份至少一个元素,可以将n个
元素排成一排,形成n-1个空隙。将m-1块隔板插入n-1个空
隙中即得m份。分配方法数:
注:隔板法使用条件有两个:(1)元素相同;
(2)每份至少一个元素(人人有份).
例2.求方程 x+y+z+w=100 的正整数解的组数.
隔板法应用之n元一次方程整数解组数问题
变式1.求方程 x+y+z+w=100 的非负整数解的组数.
分析:将每个未知数加1,令X=x+1,Y=y+1,Z=z+1,W=w+1.
方程 X+Y+Z+W=104 的正整数解的组数即为所求.
方法总结:换元法,使得每一个新元为正整数(人人有份).
方法:换元法,使得每一个新元为正整数(每份至少一个元素).
解: x+y+z+w=10变形为:(x-1)+(y-2)+(z+3)+(w+4)=14
令X=x-1,Y=y-2,Z=z+3,W=w+4,即求方程 X+Y+Z+W=14 的正整数解的组数.
隔板法应用之n元一次方程整数解组数问题
变式2.求方程 x+y+z+w=10 的整数解的组数,其中x,y,z,w分
别满足条件:x≥2,y≥3,z≥-2,w>-4.
结论:通过换元法将整数解问题化归为正整数解问题.
例1. 设有6个不同颜色的球,放入3个不同的盒子中,要求每个盒子中至少有一个球,则不同的放法有几种?
1 | 23 | 456 与 1 | 32 | 456 属同一种情况!
结论:不同元素分配问题不能使用隔板法!
型二:不同元素分配问题
X
X
例2、有4本不同的书,若全部借给3个人,每人至少1本,则不同
的借法共有( )种.
B
A错的隐秘!表示首先从4本中选3本分别给3个人,多余的一本随便发.
得两本书的那人重复计数了----误人子弟的“保底法”.
甲 乙 丙
a b cd
a b dc
丙的两本书是分先后发放的(有顺序),导致重复。解决问题的策略:先分成三组(2+1+1)再一次性分配,如答案B.
型二:不同元素分配问题
例3 有6本不同的书,分给甲、乙、丙三个人.(1)如果每人得2本,有多少种不同的分法?(2)如果其中一个人得1本,一个人得2本,一个人得3本,有多少种不同的分法?
两问区别:(1)定额定向分配,均分,(2)定额不定向分配,不均分.
法二:位置分析法(6本书即6个元素,3个人即3个位置):甲,乙,丙
结论2:不同元素分配问题通法--先分组(或堆)再分配
解:
具体分配模式有三种:①1+1+4 ②1+2+3 ③2+2+2
①1+1+4 不完全平均分
②1+2+3 不均分
③2+2+2 平均分(定额定向)
分析:不定额分配问题分类讨论化归为定额分配问题.
总分配方法数N=360+90+90=540.
结论2:不同元素分配问题通法:先分组(或堆)再分配
其中对于定额定向型分配问题也可以采用位置分析法!
回到例1. 设有6个不同颜色的球,放入3个不同的盒子中,
要求每个盒子中至少有一个球,则不同的放法有几种?
1、某学习小组有5个男生3个女生,从中选3名男生和1名女生参加
三项竞赛活动,每项活动至少有1人参加,则有不同参赛方法____种.
分析 分两步考虑, 先选人再分配(先选后排策略).
第一步 按要求取4人;
第二步 将4人分配到三项竞赛活动,分配模式:1+1+2.
不同参赛方法数N=30×36=1080.
法二、定额不定向分配,只能用先分组再分配方法.
随堂演练
2、现有3名医生和6名护士需分配到3所学校为学生体检,每校去1名医生和2名护士,不同的分配方法共有多少种?
随堂演练
法一、分两步:先分组再分配.
1°分组: 将3名医生6名护士9人按要求分成三组
首先6名护士平均分成三组再对应到三个医生(看成三个位
置)方法数:
2°分配: 将三个医护组分配到三所学校:
法二、定额定向分配,可以采用位置分析法.
例1、将4名大学生分配到A,B,C三个不同的学校实习,每个学校至
少分配一人,若甲要求不到A学校,则不同的分配方案共有 种.
型三:有限制条件的分组分配问题
A校 B校 C校
4人:甲,乙,丙,丁
分配模式:1+1+2,按甲属1人组还是2人组讨论:
甲 O OO 或 甲O O O
有限制条件的分组问题,特殊元素优先考虑 (特优法).
例2、有10名学生需分成3组,其中一组4人, 另两组3人但甲、乙不能分在同一组,有多少种不同的分组方法?
分析 10人:甲乙、 OOOOOOOO(8人)
有限制条件的分组问题,特殊元素优先考虑 (特优法).
分组模式:4+3+3. 甲乙是特殊元素,4人组是特殊位置.
分两类:①两人中一人在4人组:甲OOO,乙OO,OOO
②两人均不在4人组:OOOO,甲OO,乙OO
型三:有限制条件的分组分配问题
因为3组有区别,所以可以看成3个盒子,属于分配问题且为定额定向分配,采用位置分析法分步处理更方便!
例3、今有个人组成的旅游团,包括4个大人,2个小孩,去庐山旅游,准备同时乘缆车观光,现有三辆不同的缆车可供选择,每辆缆车最多可乘3人,为了安全起见,小孩乘缆车必须要大人陪同,则不同的乘车方式有 种.
型三:有限制条件的分组分配问题
车1 车2 车3
4大人2小孩:OOOO oo
①随意搭配
②O OO Ooo 或 O Oo OOo
③OO Oo Oo
分配模式:①3+3; ②1+2+3; ③2+2+2.
方法数为:60+216+72=348.
再见
课堂小结
1、相同元素分配问题,隔板法
2、不同元素分配问题,当元素个数多于位置个数时,总的原则是先分组再分配,属于定额定向分配问题时可采用位置分析法,根据分步计数原理,逐个逐个位置考虑。
3、含特殊元素或特殊位置情形,需要结合特优法---特殊情况优先考虑。
同课章节目录
