华东师大版数学七年级下册10.5图形的全等课件(共33张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册10.5图形的全等课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览







文档简介
课件33张PPT。回顾:上节课你学到了什么 ? 1.中心对称图形与成中心对称的概念,会判断两个图形是否成中心对称.
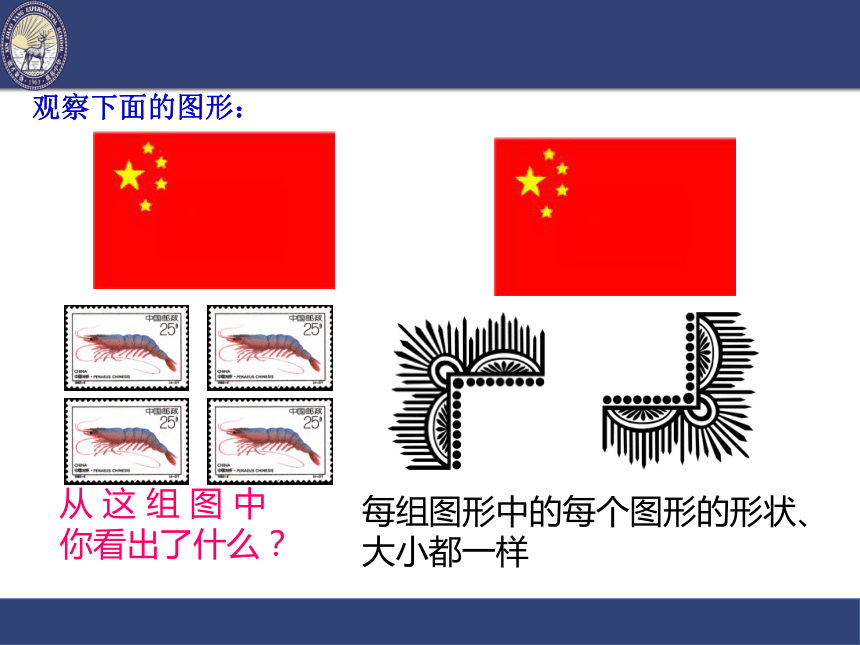
2. 成中心对称两个图形的性质,如何画一个图形关于一个点成中心对称的图形。10.5 图形的全等七年数学组观察下面的图形:从 这 组 图 中
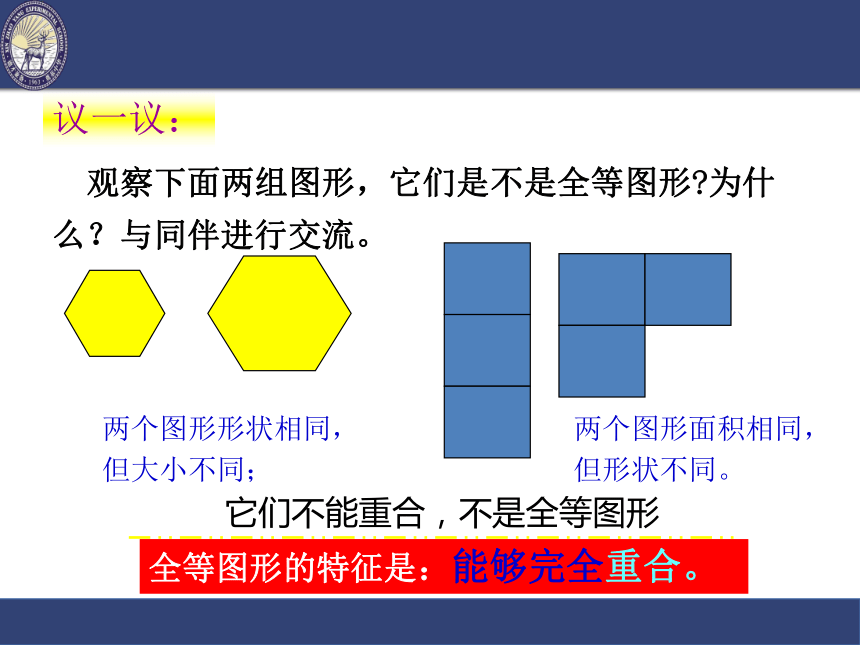
你看出了什么?每组图形中的每个图形的形状、大小都一样能够完全重合的两个图形叫做全等图形。说一说: 说说你生活中见过的全等图形的例子。议一议: 观察下面两组图形,它们是不是全等图形?为什
么?与同伴进行交流。全等图形的特征是:能够完全重合。两个图形形状相同,但大小不同;两个图形面积相同,但形状不同。它们不能重合,不是全等图形议一议: 如果两个图形全等,它们
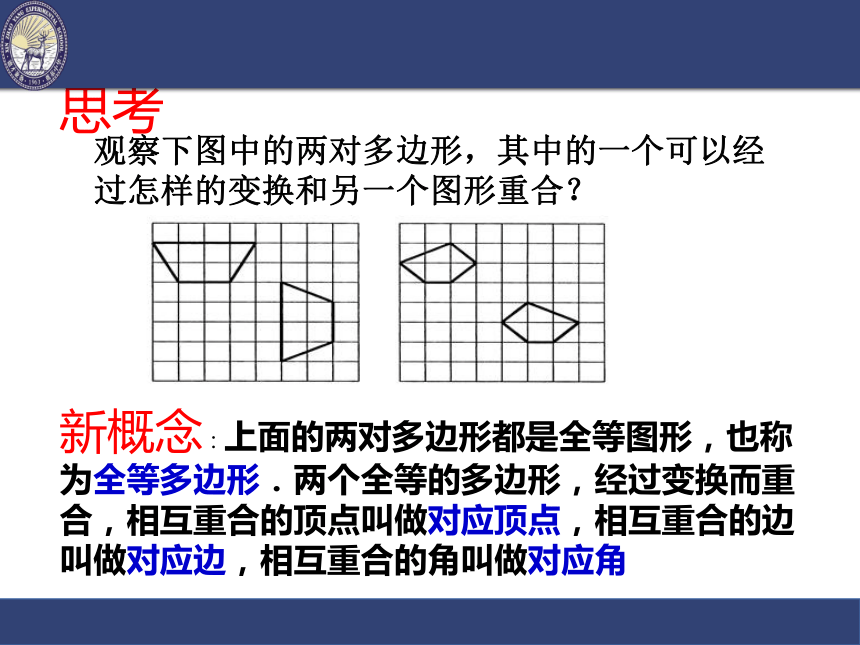
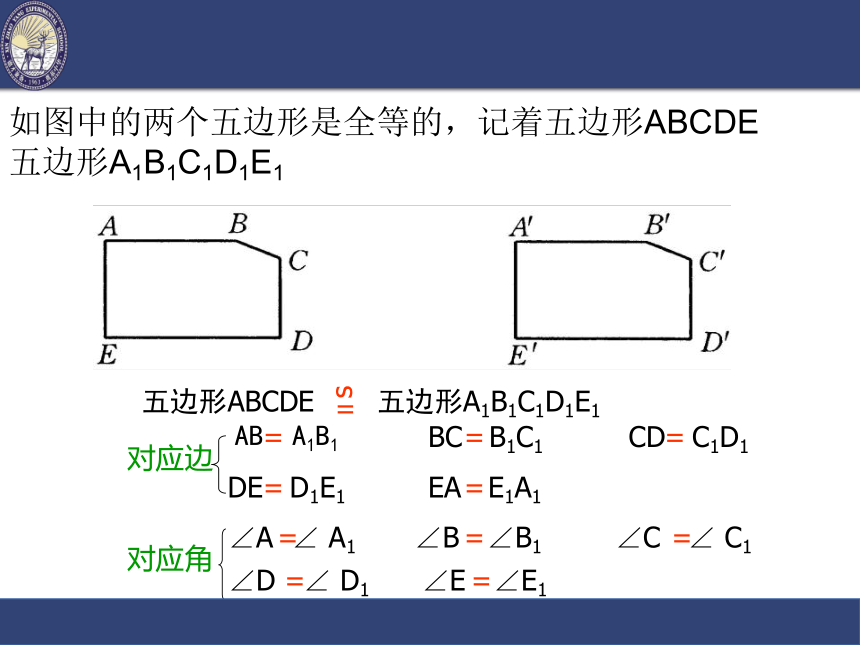
的形状与大小一定相同吗?全等图形的形状与大小都相同1.两个能够完全重合的图形称为全等图形。2.图形经过翻折、旋转或平移这三种基本的变换,前后两个图形是全等图形。3.两个全等图形经过翻折、旋转或平移这三种基本的变换后一定能够完全重合。全等图形的特征:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?思考新概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角 表示方法:记作:△ABC △ A′B′C′≌如图中的两个三角形是全等的 想一想能否记作?ABC≌ ?DEF?应该记作:?ABC≌ ?DFE原因:A与D、B与F、C与E对应。对应顶点要写在对应位置上。五边形ABCDE 五边形A1B1C1D1E1s= 对应边AB A1B1BC B1C1CD C1D1DE D1E1EA E1A1=====对应角∠A ∠ A1∠B ∠B1 ∠C ∠ C1 ∠D ∠ D1 ∠E ∠E1=====如图中的两个五边形是全等的,记着五边形ABCDE 五边形A1B1C1D1E1
全等多边形的性质:全等多边形的对应边、对应角分别相等全等多边形的判定方法:如果两个多边形的边、角分别对应相等,那么这两个多边形全等。全等三角形的性质:全等三角形的对应边、对应角分别相等全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。说一说(1)如果△ABC ≌△DEF,那么你可以得到: (2)如果具备: ∠A=∠D,∠B=∠E,∠C=∠F。ABCDEFAB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F。那么可以得出 △ABC ≌△DEF 。想一想如图,AB=DE,BC=EF,AC=DF;例1:如图△ABC沿着BC的方向平移至△DEF,∠A =800,
∠B =600,求∠F的度数。解:由图形平移的特征,可知△ABC与△DEF的形状与大小相同,即 △ABC≌△DEF ∴∠D = ∠A =800﹙全等三角形的对应角相等﹚同理 ∠DEF= ∠B =600 ∵∠D + ∠DEF+ ∠F=1800﹙三角形的内角和等于1800﹚∴∠F=1800- ∠D- ∠DEF =1800-800-600=400例2:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。解:∵ △ABC≌△DEF (已知) ∴AC=DF。(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm。 ABCDEF练一练2.如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.BDAC?4.如图,如果△ADE ≌ △CBF,那么AE∥CF吗?___ (口答“是”或“不是”)是课堂小结全等图形概念对应点、对应角、对应边性质对应角相等,对应边相等全等多边形
(全等三角形)性质:对应边、角分别相等.
判定方法:
边、角分别对应相等,则多边形(三角形)全等.补充练习做一做:沿着右边图中的虚线,分别把右面的图形划分为两个全等图形,并与同伴进行交流。
(至少找出两种方法)图形一图形二做一做:我们看看下面的几种划分方法,与你的划分方法对比一下,看看自己是如何划分的。图形一划分方法图形一划分方法做一做:做一做:图形二划分方法做一做:图形二划分方法
2. 成中心对称两个图形的性质,如何画一个图形关于一个点成中心对称的图形。10.5 图形的全等七年数学组观察下面的图形:从 这 组 图 中
你看出了什么?每组图形中的每个图形的形状、大小都一样能够完全重合的两个图形叫做全等图形。说一说: 说说你生活中见过的全等图形的例子。议一议: 观察下面两组图形,它们是不是全等图形?为什
么?与同伴进行交流。全等图形的特征是:能够完全重合。两个图形形状相同,但大小不同;两个图形面积相同,但形状不同。它们不能重合,不是全等图形议一议: 如果两个图形全等,它们
的形状与大小一定相同吗?全等图形的形状与大小都相同1.两个能够完全重合的图形称为全等图形。2.图形经过翻折、旋转或平移这三种基本的变换,前后两个图形是全等图形。3.两个全等图形经过翻折、旋转或平移这三种基本的变换后一定能够完全重合。全等图形的特征:观察下图中的两对多边形,其中的一个可以经过怎样的变换和另一个图形重合?思考新概念:上面的两对多边形都是全等图形,也称为全等多边形.两个全等的多边形,经过变换而重合,相互重合的顶点叫做对应顶点,相互重合的边叫做对应边,相互重合的角叫做对应角 表示方法:记作:△ABC △ A′B′C′≌如图中的两个三角形是全等的 想一想能否记作?ABC≌ ?DEF?应该记作:?ABC≌ ?DFE原因:A与D、B与F、C与E对应。对应顶点要写在对应位置上。五边形ABCDE 五边形A1B1C1D1E1s= 对应边AB A1B1BC B1C1CD C1D1DE D1E1EA E1A1=====对应角∠A ∠ A1∠B ∠B1 ∠C ∠ C1 ∠D ∠ D1 ∠E ∠E1=====如图中的两个五边形是全等的,记着五边形ABCDE 五边形A1B1C1D1E1
全等多边形的性质:全等多边形的对应边、对应角分别相等全等多边形的判定方法:如果两个多边形的边、角分别对应相等,那么这两个多边形全等。全等三角形的性质:全等三角形的对应边、对应角分别相等全等三角形的判定方法:如果两个三角形的边、角分别对应相等,那么这两个三角形全等。说一说(1)如果△ABC ≌△DEF,那么你可以得到: (2)如果具备: ∠A=∠D,∠B=∠E,∠C=∠F。ABCDEFAB=DE,BC=EF,AC=DF; ∠A=∠D,∠B=∠E,∠C=∠F。那么可以得出 △ABC ≌△DEF 。想一想如图,AB=DE,BC=EF,AC=DF;例1:如图△ABC沿着BC的方向平移至△DEF,∠A =800,
∠B =600,求∠F的度数。解:由图形平移的特征,可知△ABC与△DEF的形状与大小相同,即 △ABC≌△DEF ∴∠D = ∠A =800﹙全等三角形的对应角相等﹚同理 ∠DEF= ∠B =600 ∵∠D + ∠DEF+ ∠F=1800﹙三角形的内角和等于1800﹚∴∠F=1800- ∠D- ∠DEF =1800-800-600=400例2:已知△ABC≌△DEF, △ ABC的周长是40cm, AB=10cm,BC=16cm,求DF的长度。解:∵ △ABC≌△DEF (已知) ∴AC=DF。(全等三角形的对应边相等) ∵△ABC的周长是40cm, AB=10cm,BC=16cm, (已知) ∴ AC=40-10-16=14(cm), ∴ DF=14cm。 ABCDEF练一练2.如图,已知△ ABC和△ DCB全等,AB和DC是对应边,BC是公共边,说出这两个全等三角形的其他对应边和对应角以及对应顶点.BDAC?4.如图,如果△ADE ≌ △CBF,那么AE∥CF吗?___ (口答“是”或“不是”)是课堂小结全等图形概念对应点、对应角、对应边性质对应角相等,对应边相等全等多边形
(全等三角形)性质:对应边、角分别相等.
判定方法:
边、角分别对应相等,则多边形(三角形)全等.补充练习做一做:沿着右边图中的虚线,分别把右面的图形划分为两个全等图形,并与同伴进行交流。
(至少找出两种方法)图形一图形二做一做:我们看看下面的几种划分方法,与你的划分方法对比一下,看看自己是如何划分的。图形一划分方法图形一划分方法做一做:做一做:图形二划分方法做一做:图形二划分方法
