第二章第4节电源的电动势和内阻 闭合电路欧姆定律(第2课时)(共20张PPT)
文档属性
| 名称 | 第二章第4节电源的电动势和内阻 闭合电路欧姆定律(第2课时)(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 896.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-12 07:39:40 | ||
图片预览







文档简介
(共20张PPT)
2.4 电源的电动势和内阻
闭合电路欧姆定律(2)
1.电源:
基本概念和规律复习:
2.电动势:
电动势在数值上等于非静电力把单位正电荷在电源内从负极移送到正极所做的功
电动势在数值上等于电源未接入电路时两级间的电势差
电动势在数值上等于闭合电路中总的电势降落之和(内外电压之和)
3、内阻(r)
是通过非静电力做功,不断把其它形式的能转化为电势能的装置.
描述电源将其他形式的能转化为电势能能的本领,用 E 表示
4、闭合电路欧姆定律
在外电路为纯电阻的闭合电路中,电流的大小跟电源的电动势成正比,跟内、外电路的电阻之和成反比,这个规律成为闭合电路欧姆定律。
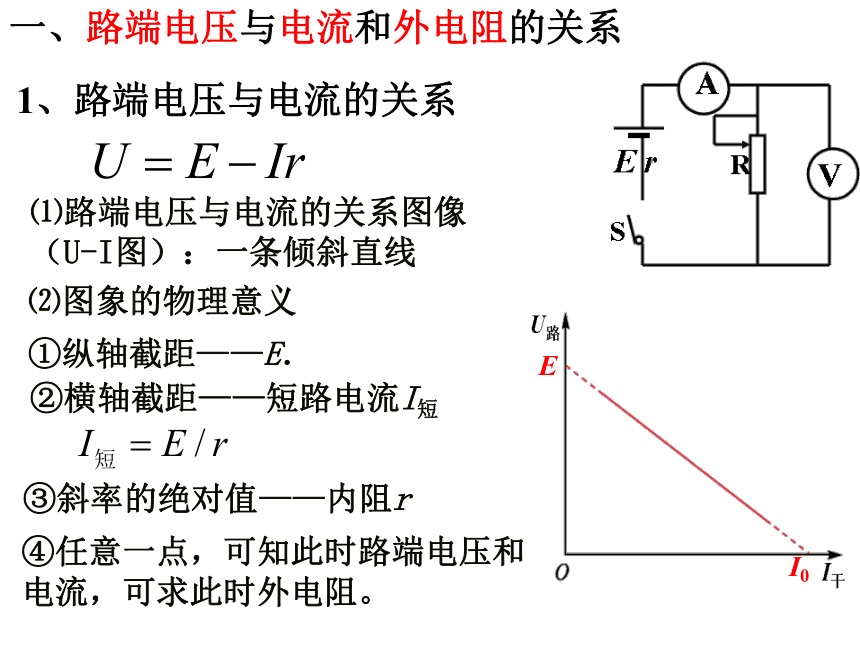
1、路端电压与电流的关系
⑴路端电压与电流的关系图像 (U-I图):一条倾斜直线
⑵图象的物理意义
①纵轴截距——E.
②横轴截距——短路电流I短
③斜率的绝对值——内阻r
E
I0
④任意一点,可知此时路端电压和电流,可求此时外电阻。
一、路端电压与电流和外电阻的关系
一、路端电压与外电阻和电流的关系
2、路端电压与外电阻的关系
① I = E /(R+ r)
② U内 =I r
③ U路= E - U内
R增大
①
I 减小
②
U内减小
③
U路增大
特例: R→∞, 外电路断开
①
I →0
②
U内=0
③
U路=E (断路)
R减小
①
I 增大
②
U内增大
③
U路减小
特例: R→0, 外电路短路
①
I =E/ r
②
U内=E
③
U路= 0 ( 短路)
典型问题:动态分析问题
解题主要策略:程序法(部分-整体-部分)
2.如图所示,电路中的电源的电动势为E、内电阻为r,开关S闭合后,当滑动变阻器的滑片P从滑动变阻器R的中点位置向左滑动时,小灯泡L1、L2、L3的亮度变化情况是( )
A. L1灯变亮,L2灯变暗,L3灯变亮
B. L1灯变暗,L2灯变亮,L3灯变暗
C. L1、L2两灯都变亮,L3灯变暗
D. L1、L2两灯都变暗,L3灯变亮
“恒定电流二”
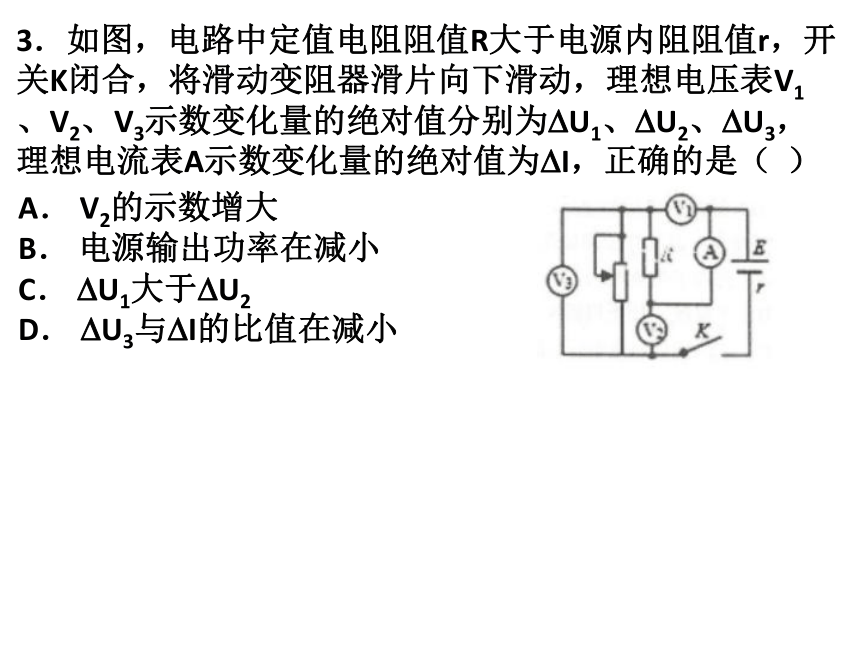
3.如图,电路中定值电阻阻值R大于电源内阻阻值r,开关K闭合,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为?U1、?U2、?U3,理想电流表A示数变化量的绝对值为?I,正确的是( )
A. V2的示数增大
B. 电源输出功率在减小
C. ?U1大于?U2
D. ?U3与?I的比值在减小
二、含电容器电路的分析与计算
1、电容器充放电结束,电路稳定后电容器所在支路可视为断路,与其串联的电阻无电流无电压,视作导线,电容器可视作理想电压表
2、注意极板正、负极
5.电源电动势为E内阻为r的电源和一个水平放置的电容为C的平行板电容器及三个电阻阻值分别为R1、R2、R3的电阻组成如图所示的电路。当开关S闭合后,电容器中有一个带电液滴正好处于静止状态,现将开关S断开,则以下判断正确的是( )
A. 液滴带正电
B. 液滴将向下运动
C. S断开前电容器上的带电荷量为
D. S断开稳定后电容器上的带电量为
6.如图电路中,电源的电动势E=3V,内阻r=1Ω,电阻R1=2Ω,R2=R4=1Ω,R3=8Ω,R5=5Ω,电容器的电容C=100μF,求闭合电键K后,通过电阻R3的总电量.
7.如图所示的电路中,闭合开关S后,灯a和b都正常发光, 后来由于某种故障使灯b突然变亮,电压表读数增加,由此推断这故障可能是( )
A. 电阻R2断路
B. 电阻R2短路
C. a灯灯丝烧断
D. 电容被击穿短路
三、故障电路的分析
8.如图所示,因线路故障,接通S时,灯泡L1和L2均不亮,用电压表测得Uab=0,Ubc=0,Ucd=4 V.因此可知开路处为 ( )
A. 灯泡L1 B. 灯泡L2
C. 变阻器 D. 不能确定
用电压表检测故障:
1、有示数:与其串联的支路无段路,并联的支路无短路
2、无示数,情况可能正好相反
2.4 电源的电动势和内阻
闭合电路欧姆定律(2)
1.电源:
基本概念和规律复习:
2.电动势:
电动势在数值上等于非静电力把单位正电荷在电源内从负极移送到正极所做的功
电动势在数值上等于电源未接入电路时两级间的电势差
电动势在数值上等于闭合电路中总的电势降落之和(内外电压之和)
3、内阻(r)
是通过非静电力做功,不断把其它形式的能转化为电势能的装置.
描述电源将其他形式的能转化为电势能能的本领,用 E 表示
4、闭合电路欧姆定律
在外电路为纯电阻的闭合电路中,电流的大小跟电源的电动势成正比,跟内、外电路的电阻之和成反比,这个规律成为闭合电路欧姆定律。
1、路端电压与电流的关系
⑴路端电压与电流的关系图像 (U-I图):一条倾斜直线
⑵图象的物理意义
①纵轴截距——E.
②横轴截距——短路电流I短
③斜率的绝对值——内阻r
E
I0
④任意一点,可知此时路端电压和电流,可求此时外电阻。
一、路端电压与电流和外电阻的关系
一、路端电压与外电阻和电流的关系
2、路端电压与外电阻的关系
① I = E /(R+ r)
② U内 =I r
③ U路= E - U内
R增大
①
I 减小
②
U内减小
③
U路增大
特例: R→∞, 外电路断开
①
I →0
②
U内=0
③
U路=E (断路)
R减小
①
I 增大
②
U内增大
③
U路减小
特例: R→0, 外电路短路
①
I =E/ r
②
U内=E
③
U路= 0 ( 短路)
典型问题:动态分析问题
解题主要策略:程序法(部分-整体-部分)
2.如图所示,电路中的电源的电动势为E、内电阻为r,开关S闭合后,当滑动变阻器的滑片P从滑动变阻器R的中点位置向左滑动时,小灯泡L1、L2、L3的亮度变化情况是( )
A. L1灯变亮,L2灯变暗,L3灯变亮
B. L1灯变暗,L2灯变亮,L3灯变暗
C. L1、L2两灯都变亮,L3灯变暗
D. L1、L2两灯都变暗,L3灯变亮
“恒定电流二”
3.如图,电路中定值电阻阻值R大于电源内阻阻值r,开关K闭合,将滑动变阻器滑片向下滑动,理想电压表V1、V2、V3示数变化量的绝对值分别为?U1、?U2、?U3,理想电流表A示数变化量的绝对值为?I,正确的是( )
A. V2的示数增大
B. 电源输出功率在减小
C. ?U1大于?U2
D. ?U3与?I的比值在减小
二、含电容器电路的分析与计算
1、电容器充放电结束,电路稳定后电容器所在支路可视为断路,与其串联的电阻无电流无电压,视作导线,电容器可视作理想电压表
2、注意极板正、负极
5.电源电动势为E内阻为r的电源和一个水平放置的电容为C的平行板电容器及三个电阻阻值分别为R1、R2、R3的电阻组成如图所示的电路。当开关S闭合后,电容器中有一个带电液滴正好处于静止状态,现将开关S断开,则以下判断正确的是( )
A. 液滴带正电
B. 液滴将向下运动
C. S断开前电容器上的带电荷量为
D. S断开稳定后电容器上的带电量为
6.如图电路中,电源的电动势E=3V,内阻r=1Ω,电阻R1=2Ω,R2=R4=1Ω,R3=8Ω,R5=5Ω,电容器的电容C=100μF,求闭合电键K后,通过电阻R3的总电量.
7.如图所示的电路中,闭合开关S后,灯a和b都正常发光, 后来由于某种故障使灯b突然变亮,电压表读数增加,由此推断这故障可能是( )
A. 电阻R2断路
B. 电阻R2短路
C. a灯灯丝烧断
D. 电容被击穿短路
三、故障电路的分析
8.如图所示,因线路故障,接通S时,灯泡L1和L2均不亮,用电压表测得Uab=0,Ubc=0,Ucd=4 V.因此可知开路处为 ( )
A. 灯泡L1 B. 灯泡L2
C. 变阻器 D. 不能确定
用电压表检测故障:
1、有示数:与其串联的支路无段路,并联的支路无短路
2、无示数,情况可能正好相反
同课章节目录
