北师大版九年级数学下册3.7切线长定理同步测试(附答案)
文档属性
| 名称 | 北师大版九年级数学下册3.7切线长定理同步测试(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览


文档简介
3.7 切线长定理
同步测试
选择题
1.如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ,则∠EDC的度数为(?? )
A.?60°????B.?90°???C.?30°??D.?75°
2.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A. B. C. D.
4.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为(? ).
A.1:5??????B.2:5???C.3:5????D.?4:5
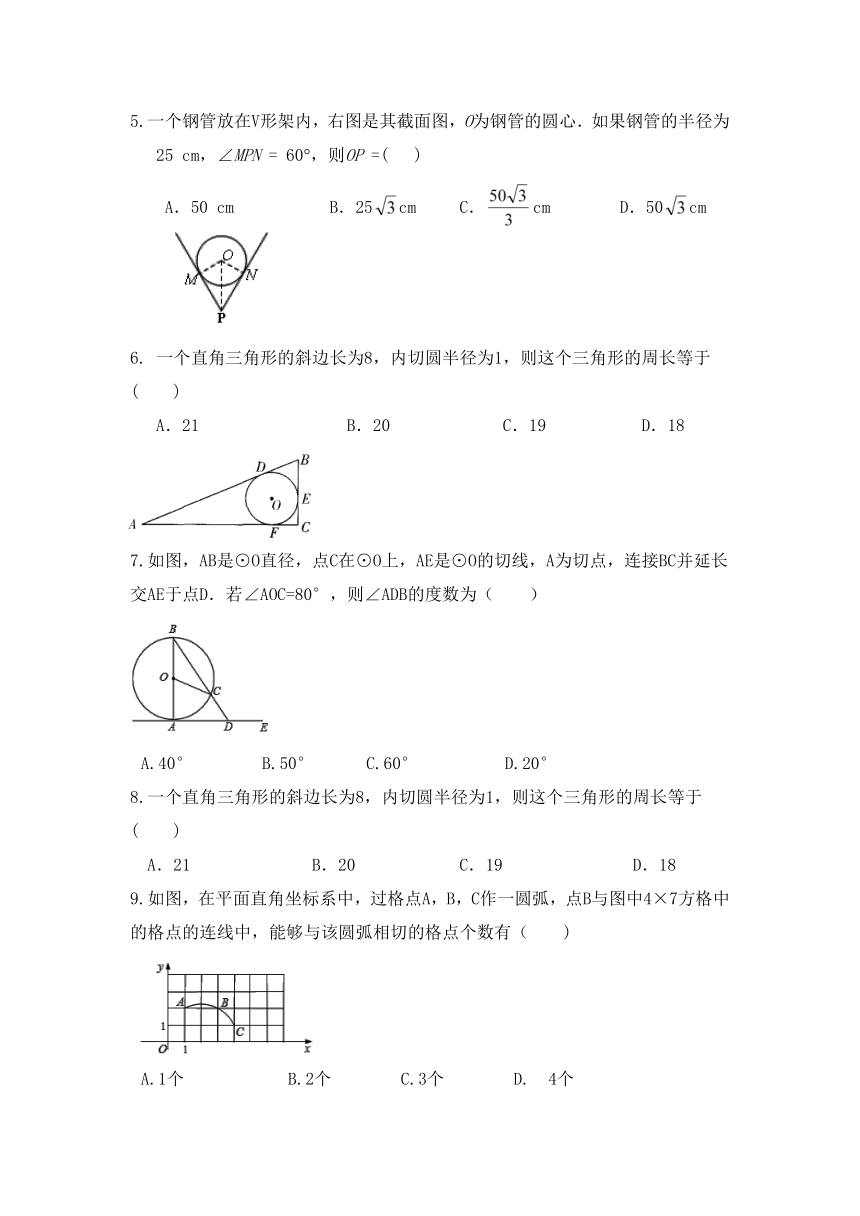
5.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm,∠MPN = 60(,则OP =( )
A.50 cm B.25cm C.cm D.50cm
6. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
7.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40°????B.50°???C.60°?????D.20°
8.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
9.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有( )
A.1个??????B.2个????C.3个????D.?4个
10.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是( )
A.?20°???B.?25°???C.?30°??D.?35°
填空题
11.如图,在△ABC中,,cosB.如果⊙O的半径为cm,且经过点B、C,那么线段AO= cm.
12.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则
∠BOC= .
14.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
15.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠ACB=70°,那么∠OPA的度数是________度.
综合题
16. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
17.如图,AB是(O的直径,点P是BA延长线上一点,过点P作(O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.
(1)求证:PD是(O的切线;
(2)若AB=10,tanB=,求PA的长;
18.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
(1)求证:∠ABC=∠CBD;
(2)若BC=4,CD=4,则⊙O的半径是 .
19.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,求DM的长.
3.7 切线长定理
同步测试答案
选择题
1.A 2.C 3.A 4.C 5.D 6.B 7.C 8.C 9.D 10.B
二、填空题
11.
12.200 4
13.1100
14.52
15.200
三、综合题
16.解:(1)∵在△ABO中,OA=OB,∠OAB=30°
∴∠AOB=180°-2×30°=120°????
∵PA、PB是⊙O的切线
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°
∴在四边形OAPB中,
∠APB=360°-120°-90°-90°=60°.???
(2)如图①,连结OP?? ???
∵PA、PB是⊙O的切线
∴PO平分∠APB,即∠APO=∠APB=30°
又∵在Rt△OAP中,OA=3, ∠APO=30°
∴AP==3.
17.解:(1)连接OD,∵CD⊥AB,∴CE=ED,∴PC=PD,∵OC=OD,∴△POC≌△POD,∴∠PDO=∠PCO,∵PC是(O的切线,∴PC⊥OC,∠PCO=90°,∴∠PDO=90°,∴PD⊥DO,∴PD是(O的切线;
(2)连接AC,∵tanB=,∴设AC=x,则BC=2x,∵AB=10,∴AO=CO=5,在Rt△ABC中,由勾股定理可求得:AC=,BC=,∴CE=4,EO=3,∵△COE∽△POC,∴PO=,∴AP=PO-AO=;
18.(1)证明:连接OC,
∵MN为⊙O的切线,
∴OC⊥MN,
∵BD⊥MN,
∴OC∥BD,
∴∠CBD=∠BCO.
又∵OC=OB,
∴∠BCO=∠ABC,
∴∠CBD=∠ABC.;
(2)解:连接AC,
在Rt△BCD中,BC=4,CD=4,
∴BD=8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠CDB=90°,
∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴,即=,
∴AB=10,
∴⊙O的半径是5,
故答案为5.
19.解:连接OE,OF,ON,OG.∵四边形ABCD是矩形,∴∠A=∠B=90°,CD=AB=4.∵AD,AB,BC分别与⊙O相切于E,F,G三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,OE=OF=OG,∴四边形AFOE,FBGO是正方形,∴AF=BF=AE=BG=2,∴DE=3.∵DM是⊙O的切线,∴DN=DE=3,MN=MG,∴CM=BC-BG-MG=5-2-MN=3-MN.在Rt△DMC中,DM2=CD2+CM2,∴(3+MN)2=42+(3-MN)2,∴MN=,∴DM=3+=.
同步测试
选择题
1.如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ,则∠EDC的度数为(?? )
A.?60°????B.?90°???C.?30°??D.?75°
2.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,
则与∠PAB相等的角(不包括∠PAB本身)有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=2,以AB的中点O为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A. B. C. D.
4.边长分别为3,4,5的三角形的内切圆半径与外接圆的半径之比为(? ).
A.1:5??????B.2:5???C.3:5????D.?4:5
5.一个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm,∠MPN = 60(,则OP =( )
A.50 cm B.25cm C.cm D.50cm
6. 一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
7.如图,AB是⊙O直径,点C在⊙O上,AE是⊙O的切线,A为切点,连接BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( )
A.40°????B.50°???C.60°?????D.20°
8.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )
A.21 B.20 C.19 D.18
9.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中4×7方格中的格点的连线中,能够与该圆弧相切的格点个数有( )
A.1个??????B.2个????C.3个????D.?4个
10.如图,AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC.若∠P=20°,则∠B的度数是( )
A.?20°???B.?25°???C.?30°??D.?35°
填空题
11.如图,在△ABC中,,cosB.如果⊙O的半径为cm,且经过点B、C,那么线段AO= cm.
12.如图,PA、PB是⊙O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
如图,已知点O是△ABC 的内心,且∠ABC= 60 °, ∠ACB= 80 °,则
∠BOC= .
14.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
15.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在⊙O上,如果∠ACB=70°,那么∠OPA的度数是________度.
综合题
16. 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
17.如图,AB是(O的直径,点P是BA延长线上一点,过点P作(O的切线PC,切点是C,过点C作弦CD⊥AB于E,连接CO,CB.
(1)求证:PD是(O的切线;
(2)若AB=10,tanB=,求PA的长;
18.如图,AB是⊙O的直径,BC是⊙O的弦,直线MN与⊙O相切于点C,过点B作BD⊥MN于点D.
(1)求证:∠ABC=∠CBD;
(2)若BC=4,CD=4,则⊙O的半径是 .
19.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,求DM的长.
3.7 切线长定理
同步测试答案
选择题
1.A 2.C 3.A 4.C 5.D 6.B 7.C 8.C 9.D 10.B
二、填空题
11.
12.200 4
13.1100
14.52
15.200
三、综合题
16.解:(1)∵在△ABO中,OA=OB,∠OAB=30°
∴∠AOB=180°-2×30°=120°????
∵PA、PB是⊙O的切线
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°
∴在四边形OAPB中,
∠APB=360°-120°-90°-90°=60°.???
(2)如图①,连结OP?? ???
∵PA、PB是⊙O的切线
∴PO平分∠APB,即∠APO=∠APB=30°
又∵在Rt△OAP中,OA=3, ∠APO=30°
∴AP==3.
17.解:(1)连接OD,∵CD⊥AB,∴CE=ED,∴PC=PD,∵OC=OD,∴△POC≌△POD,∴∠PDO=∠PCO,∵PC是(O的切线,∴PC⊥OC,∠PCO=90°,∴∠PDO=90°,∴PD⊥DO,∴PD是(O的切线;
(2)连接AC,∵tanB=,∴设AC=x,则BC=2x,∵AB=10,∴AO=CO=5,在Rt△ABC中,由勾股定理可求得:AC=,BC=,∴CE=4,EO=3,∵△COE∽△POC,∴PO=,∴AP=PO-AO=;
18.(1)证明:连接OC,
∵MN为⊙O的切线,
∴OC⊥MN,
∵BD⊥MN,
∴OC∥BD,
∴∠CBD=∠BCO.
又∵OC=OB,
∴∠BCO=∠ABC,
∴∠CBD=∠ABC.;
(2)解:连接AC,
在Rt△BCD中,BC=4,CD=4,
∴BD=8,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠CDB=90°,
∵∠ABC=∠CBD,
∴△ABC∽△CBD,
∴,即=,
∴AB=10,
∴⊙O的半径是5,
故答案为5.
19.解:连接OE,OF,ON,OG.∵四边形ABCD是矩形,∴∠A=∠B=90°,CD=AB=4.∵AD,AB,BC分别与⊙O相切于E,F,G三点,∴∠AEO=∠AFO=∠OFB=∠BGO=90°,OE=OF=OG,∴四边形AFOE,FBGO是正方形,∴AF=BF=AE=BG=2,∴DE=3.∵DM是⊙O的切线,∴DN=DE=3,MN=MG,∴CM=BC-BG-MG=5-2-MN=3-MN.在Rt△DMC中,DM2=CD2+CM2,∴(3+MN)2=42+(3-MN)2,∴MN=,∴DM=3+=.
