人教版数学八年级下册 17.1勾股定理 同步练习 (解析版)
文档属性
| 名称 | 人教版数学八年级下册 17.1勾股定理 同步练习 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 333.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 06:48:43 | ||
图片预览


文档简介
人教版八年级下册 17.1勾股定理 同步练习
一、单选题
1.我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A. B. C. D.
2.在中,,若,,则的长为( )
A. B.5 C.6 D.7
3.下列说法正确的是( ).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
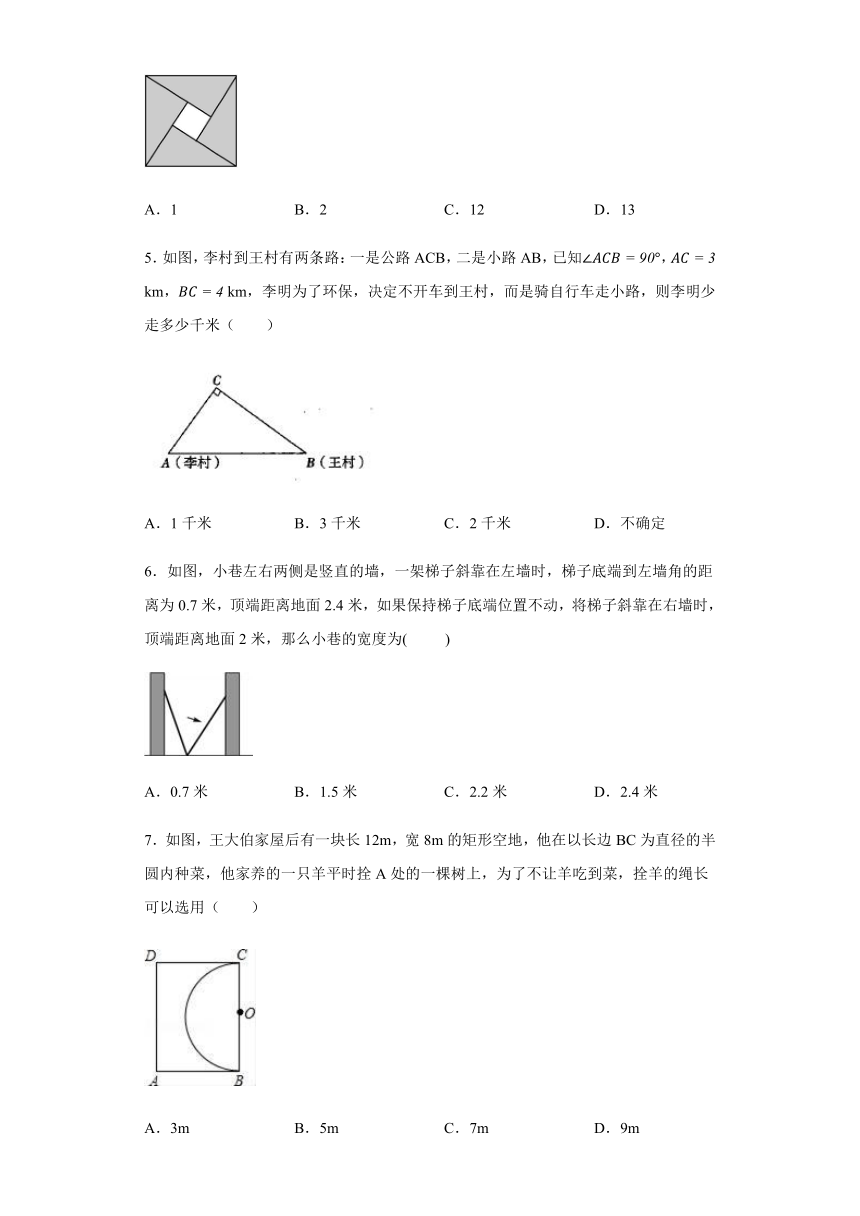
4.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是( )
A.1 B.2 C.12 D.13
5.如图,李村到王村有两条路:一是公路ACB,二是小路AB,已知, km, km,李明为了环保,决定不开车到王村,而是骑自行车走小路,则李明少走多少千米( )
A.1千米 B.3千米 C.2千米 D.不确定
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
7.如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3m B.5m C.7m D.9m
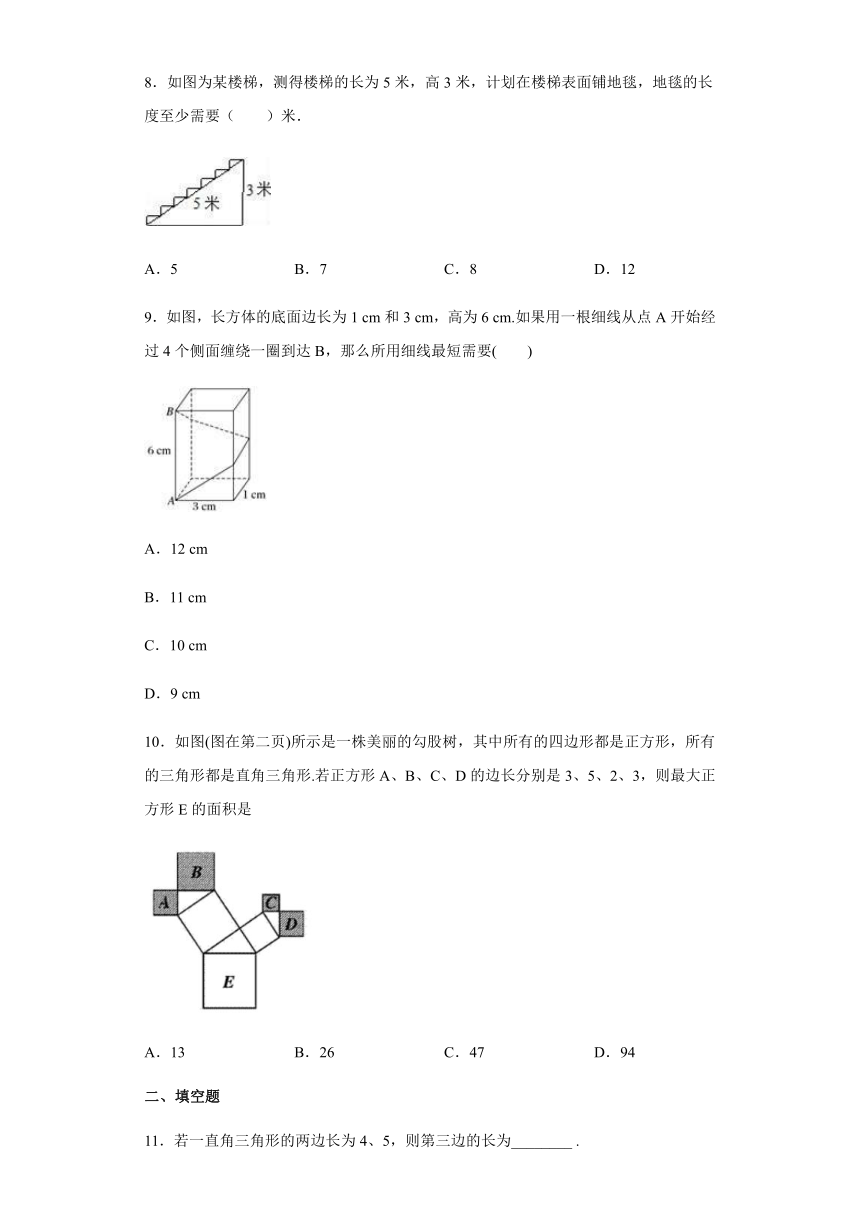
8.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
A.5 B.7 C.8 D.12
9.如图,长方体的底面边长为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
A.12 cm
B.11 cm
C.10 cm
D.9 cm
10.如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
A.13 B.26 C.47 D.94
二、填空题
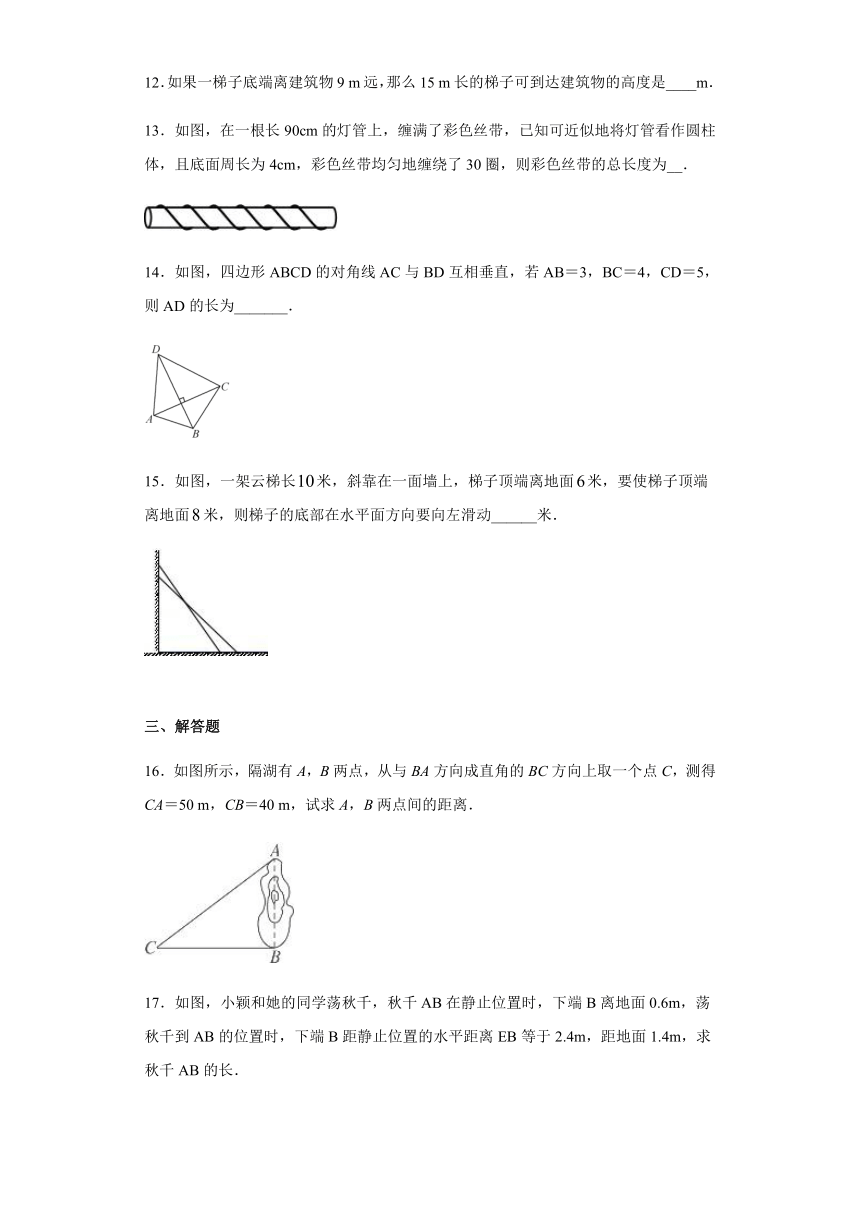
11.若一直角三角形的两边长为4、5,则第三边的长为________ .
12.如果一梯子底端离建筑物9 m远,那么15 m长的梯子可到达建筑物的高度是____m.
13.如图,在一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为__.
14.如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为_______.
15.如图,一架云梯长米,斜靠在一面墙上,梯子顶端离地面米,要使梯子顶端离地面米,则梯子的底部在水平面方向要向左滑动______米.
三、解答题
16.如图所示,隔湖有A,B两点,从与BA方向成直角的BC方向上取一个点C,测得CA=50 m,CB=40 m,试求A,B两点间的距离.
17.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
18.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方m处,过了2s后,测得小汽车与车速检测仪间距离为m,这辆小汽车超速了吗?
19.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
20.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?
21.一架方梯AB长25米,如图所示,斜靠在一面上:
(1)若梯子底端离墙OB=7米,这个梯子的顶端距地面AO有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了BB?几米?
参考答案
1.C
【解析】
解:A、有三个直角三角形, 其面积分别为ab,ab和,
还可以理解为一个直角梯形,其面积为,由图形可知:
=ab+ab+,
整理得:(a+b)=2ab+c,a+b+2ab=2ab+ c, a+b= c
能证明勾股定理;
B、中间正方形的面积= c,中间正方形的面积=(a+b)-4ab=a+b,
a+b= c,能证明勾股定理;
C、不能利用图形面积证明勾股定理, 它是对完全平方公式的说明.
D、大正方形的面积= c,大正方形的面积=(b-a)+4ab = a+b,,
a+b= c,能证明勾股定理;
故选C.
2.B
【解析】
在直角△ABC中,∠C=90°,由勾股定理可得,所以.故选B.
3.D
【解析】
解:由勾股定理,
A、没有确定直角和斜边,故A 错误;
B、没有确定斜边,故B错误;
C、斜边为,则,故C错误;
D、,则与为直角边,为斜边,则,故D正确;
故选择:D.
4.A
【解析】
根据勾股定理可得a2+b2=13
四个直角三角形的面积是:ab×4=13?1=12,即:2ab=12
则(a?b)2=a2?2ab+b2=13?12=1
故选:A
5.C
【解析】
解:∵,,,
∴,
∴(km),
故选C.
6.C
【解析】
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+22=6.25,∴BD2=2.25,∵BD>0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.故选C.
7.A
【解析】
解:连接OA,交⊙O于E点,
在Rt△OAB中,OB=6,AB=8,
所以OA==10;
又OE=OB=6,
所以AE=OA-OE=4.
因此选用的绳子应该不大于4,
故选A.
8.B
【解析】
根据勾股定理求得楼梯的水平宽度==4,然后由地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,地毯的长度至少是3+4=7米.故选B.
9.C
【解析】
解:将长方体展开,连接A、B,
根据两点之间线段最短,AB==10(cm).
故选C.
10.C
【解析】
解:如图
根据勾股定理的几何意义,可得A、B的面积和为,C、D的面积和为,,于是,即故选C.
11. 或3
【解析】
解:当4和5都是直角边时,则第三边是 ;
当5是斜边时,则第三边是 ;
故答案是:和3.
12.12
【解析】
∵直角三角形的斜边长为15m,一直角边长为9m,
∴另一直角边长=,
故梯子可到达建筑物的高度是12m.
故答案是:12m.
13.150cm
【解析】
如图,彩色丝带的总长度为=150cm.
14.3
【解析】
在Rt△AOB中,= ?;
Rt△DOC中可得:=?;
∴=+
= –+?
= –+
= –
=18,
即可得AD==3.故答案为3.
15.
【解析】
如图,AB=DE=10,AC=6,DC=8,∠C =90°,
∴BC==8,
CE==6,
∴BE=BC-CE=2(米),
故答案为2.
16.A,B两点间的距离是30 m.
【解析】
由图可知,三角形ABC是直角三角形.
∵CA=50m,CB=40m,∴AB30(m).
答:A,B两点间的距离是30 m.
17.4m
【解析】
由题意可得出:B′E=1.4﹣0.6=0.8(m),
则AE=AB﹣0.8,
在Rt△AEB中,
AE2+BE2=AB2,
∴(AB﹣0.8)2+2.42=AB2
解得:AB=4,
答:秋千AB的长为4m.
18.见解析
【解析】
解:在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:
BC==40(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
19.(1)DE=3;(2).
【解析】
(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,由勾股定理得:,
∴△ADB的面积为.
20.(1)它爬行一圈的路程是50cm;(2)树干高6m.
【解析】
解:(1)如图为圆柱侧面沿AB剪开的展开图.
圆柱的底面周长为30cm,即AC=30cm,高为40cm,即CD=40cm,
∴AD==50cm.
答:它爬行一圈的路程是50cm.
(2)树干的周长为80cm,即AC=80cm,绕一圈爬行100cm,即AD=100cm,
∴绕一圈上升的高度CD==60cm.
∴树干的高为60×10=600(cm)=6(m).
答:树干高6m.
21.(1)24米;(2)8.
【解析】
(1)在Rt△AOB中,AB=25米,OB=7米,OA24(米).
答:梯子的顶端距地面24米;
(2)在Rt△AOB中,A'O=24﹣4=20米,OB'15(米),BB'=15﹣7=8米.
答:梯子的底端在水平方向滑动了8米.
一、单选题
1.我国是最早了解勾股定理的国家之一.下面四幅图中,不能用来证明勾股定理的是( )
A. B. C. D.
2.在中,,若,,则的长为( )
A. B.5 C.6 D.7
3.下列说法正确的是( ).
A.若、、是的三边长,则
B.若、、是的三边长,则
C.若、、是的三边长,,则
D.若、、是的三边长,,则
4.我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是( )
A.1 B.2 C.12 D.13
5.如图,李村到王村有两条路:一是公路ACB,二是小路AB,已知, km, km,李明为了环保,决定不开车到王村,而是骑自行车走小路,则李明少走多少千米( )
A.1千米 B.3千米 C.2千米 D.不确定
6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
7.如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
A.3m B.5m C.7m D.9m
8.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要( )米.
A.5 B.7 C.8 D.12
9.如图,长方体的底面边长为1 cm和3 cm,高为6 cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B,那么所用细线最短需要( )
A.12 cm
B.11 cm
C.10 cm
D.9 cm
10.如图(图在第二页)所示是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是
A.13 B.26 C.47 D.94
二、填空题
11.若一直角三角形的两边长为4、5,则第三边的长为________ .
12.如果一梯子底端离建筑物9 m远,那么15 m长的梯子可到达建筑物的高度是____m.
13.如图,在一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为__.
14.如图,四边形ABCD的对角线AC与BD互相垂直,若AB=3,BC=4,CD=5,则AD的长为_______.
15.如图,一架云梯长米,斜靠在一面墙上,梯子顶端离地面米,要使梯子顶端离地面米,则梯子的底部在水平面方向要向左滑动______米.
三、解答题
16.如图所示,隔湖有A,B两点,从与BA方向成直角的BC方向上取一个点C,测得CA=50 m,CB=40 m,试求A,B两点间的距离.
17.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
18.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方m处,过了2s后,测得小汽车与车速检测仪间距离为m,这辆小汽车超速了吗?
19.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
20.葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?
21.一架方梯AB长25米,如图所示,斜靠在一面上:
(1)若梯子底端离墙OB=7米,这个梯子的顶端距地面AO有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了BB?几米?
参考答案
1.C
【解析】
解:A、有三个直角三角形, 其面积分别为ab,ab和,
还可以理解为一个直角梯形,其面积为,由图形可知:
=ab+ab+,
整理得:(a+b)=2ab+c,a+b+2ab=2ab+ c, a+b= c
能证明勾股定理;
B、中间正方形的面积= c,中间正方形的面积=(a+b)-4ab=a+b,
a+b= c,能证明勾股定理;
C、不能利用图形面积证明勾股定理, 它是对完全平方公式的说明.
D、大正方形的面积= c,大正方形的面积=(b-a)+4ab = a+b,,
a+b= c,能证明勾股定理;
故选C.
2.B
【解析】
在直角△ABC中,∠C=90°,由勾股定理可得,所以.故选B.
3.D
【解析】
解:由勾股定理,
A、没有确定直角和斜边,故A 错误;
B、没有确定斜边,故B错误;
C、斜边为,则,故C错误;
D、,则与为直角边,为斜边,则,故D正确;
故选择:D.
4.A
【解析】
根据勾股定理可得a2+b2=13
四个直角三角形的面积是:ab×4=13?1=12,即:2ab=12
则(a?b)2=a2?2ab+b2=13?12=1
故选:A
5.C
【解析】
解:∵,,,
∴,
∴(km),
故选C.
6.C
【解析】
在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+22=6.25,∴BD2=2.25,∵BD>0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.故选C.
7.A
【解析】
解:连接OA,交⊙O于E点,
在Rt△OAB中,OB=6,AB=8,
所以OA==10;
又OE=OB=6,
所以AE=OA-OE=4.
因此选用的绳子应该不大于4,
故选A.
8.B
【解析】
根据勾股定理求得楼梯的水平宽度==4,然后由地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,地毯的长度至少是3+4=7米.故选B.
9.C
【解析】
解:将长方体展开,连接A、B,
根据两点之间线段最短,AB==10(cm).
故选C.
10.C
【解析】
解:如图
根据勾股定理的几何意义,可得A、B的面积和为,C、D的面积和为,,于是,即故选C.
11. 或3
【解析】
解:当4和5都是直角边时,则第三边是 ;
当5是斜边时,则第三边是 ;
故答案是:和3.
12.12
【解析】
∵直角三角形的斜边长为15m,一直角边长为9m,
∴另一直角边长=,
故梯子可到达建筑物的高度是12m.
故答案是:12m.
13.150cm
【解析】
如图,彩色丝带的总长度为=150cm.
14.3
【解析】
在Rt△AOB中,= ?;
Rt△DOC中可得:=?;
∴=+
= –+?
= –+
= –
=18,
即可得AD==3.故答案为3.
15.
【解析】
如图,AB=DE=10,AC=6,DC=8,∠C =90°,
∴BC==8,
CE==6,
∴BE=BC-CE=2(米),
故答案为2.
16.A,B两点间的距离是30 m.
【解析】
由图可知,三角形ABC是直角三角形.
∵CA=50m,CB=40m,∴AB30(m).
答:A,B两点间的距离是30 m.
17.4m
【解析】
由题意可得出:B′E=1.4﹣0.6=0.8(m),
则AE=AB﹣0.8,
在Rt△AEB中,
AE2+BE2=AB2,
∴(AB﹣0.8)2+2.42=AB2
解得:AB=4,
答:秋千AB的长为4m.
18.见解析
【解析】
解:在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:
BC==40(m)
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h);
∵72(km/h)>70(km/h);
∴这辆小汽车超速行驶.
答:这辆小汽车超速了.
19.(1)DE=3;(2).
【解析】
(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,由勾股定理得:,
∴△ADB的面积为.
20.(1)它爬行一圈的路程是50cm;(2)树干高6m.
【解析】
解:(1)如图为圆柱侧面沿AB剪开的展开图.
圆柱的底面周长为30cm,即AC=30cm,高为40cm,即CD=40cm,
∴AD==50cm.
答:它爬行一圈的路程是50cm.
(2)树干的周长为80cm,即AC=80cm,绕一圈爬行100cm,即AD=100cm,
∴绕一圈上升的高度CD==60cm.
∴树干的高为60×10=600(cm)=6(m).
答:树干高6m.
21.(1)24米;(2)8.
【解析】
(1)在Rt△AOB中,AB=25米,OB=7米,OA24(米).
答:梯子的顶端距地面24米;
(2)在Rt△AOB中,A'O=24﹣4=20米,OB'15(米),BB'=15﹣7=8米.
答:梯子的底端在水平方向滑动了8米.
