苏科版八年级数学下册:9.1 图形的旋转 培优练习(含答案)
文档属性
| 名称 | 苏科版八年级数学下册:9.1 图形的旋转 培优练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 349.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 20:50:30 | ||
图片预览


文档简介
苏科版(2012)八年级数学下册9.1图形的旋转培优练习
一、单选题
1.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.在成中心对称的两个图形中,连结对称点的线段都被对称中心平分
C.在平面直角坐标系中,一点向右平移2个单位,纵坐标加2
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
2.如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(﹣2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
A.(1,﹣1) B.(1,1) C.(﹣1,1) D.(﹣1,﹣1)
3.王涵将如图1所示的等边三角形绕三条角平分线的交点旋转一定角度后可得到如图2所示的图形,则王涵的旋转方法可以是( )
A.逆时针旋转 B.顺时针旋转 C.逆时针旋转 D.顺时针旋转
4.如图,紫荆花绕自己的旋转中心,按下列角度旋转,不能与其自身重合的是( )
A. B. C. D.
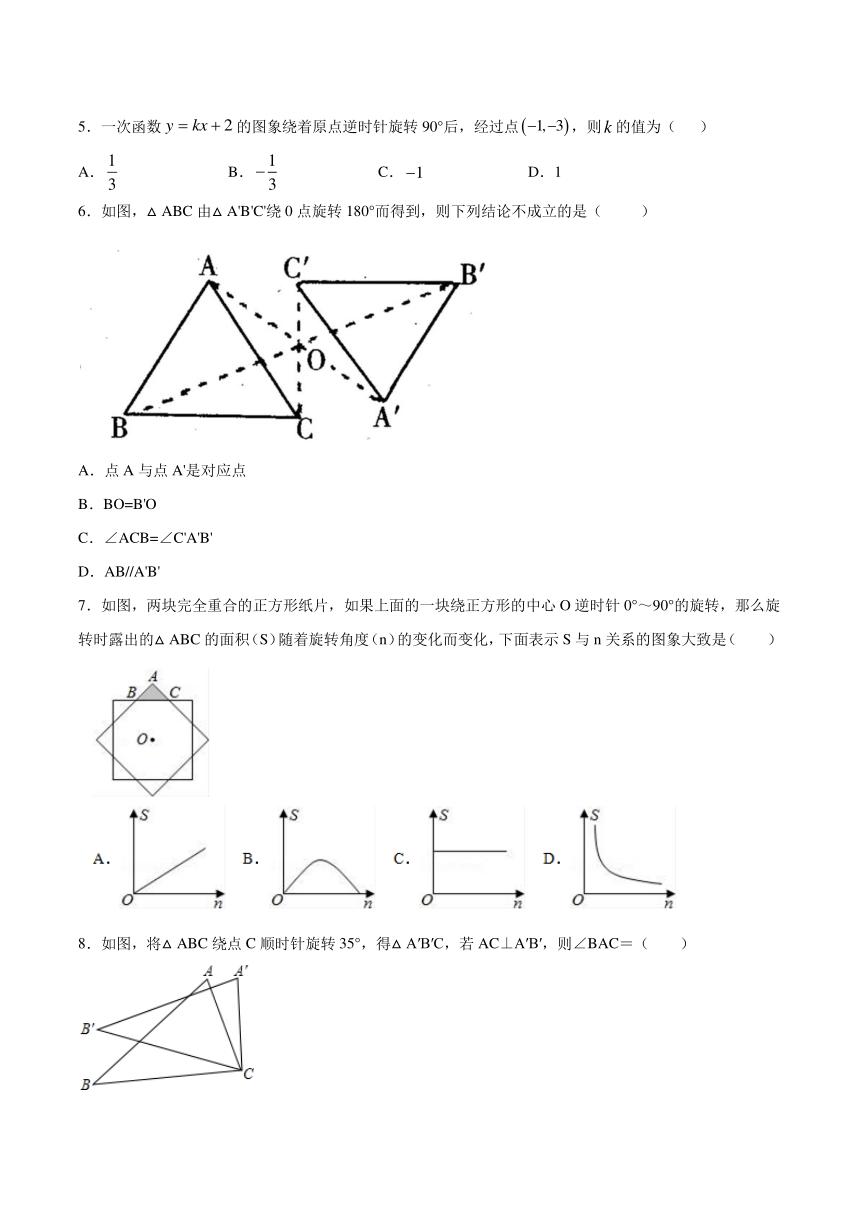
5.一次函数的图象绕着原点逆时针旋转90°后,经过点,则的值为( )
A. B. C. D.1
6.如图,△ABC由△A'B'C'绕0点旋转180°而得到,则下列结论不成立的是( )
A.点A与点A'是对应点
B.BO=B'O
C.∠ACB=∠C'A'B'
D.AB//A'B'
7.如图,两块完全重合的正方形纸片,如果上面的一块绕正方形的中心O逆时针0°~90°的旋转,那么旋转时露出的△ABC的面积(S)随着旋转角度(n)的变化而变化,下面表示S与n关系的图象大致是( )
8.如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )
A.65° B.75° C.55° D.35°
二、填空题
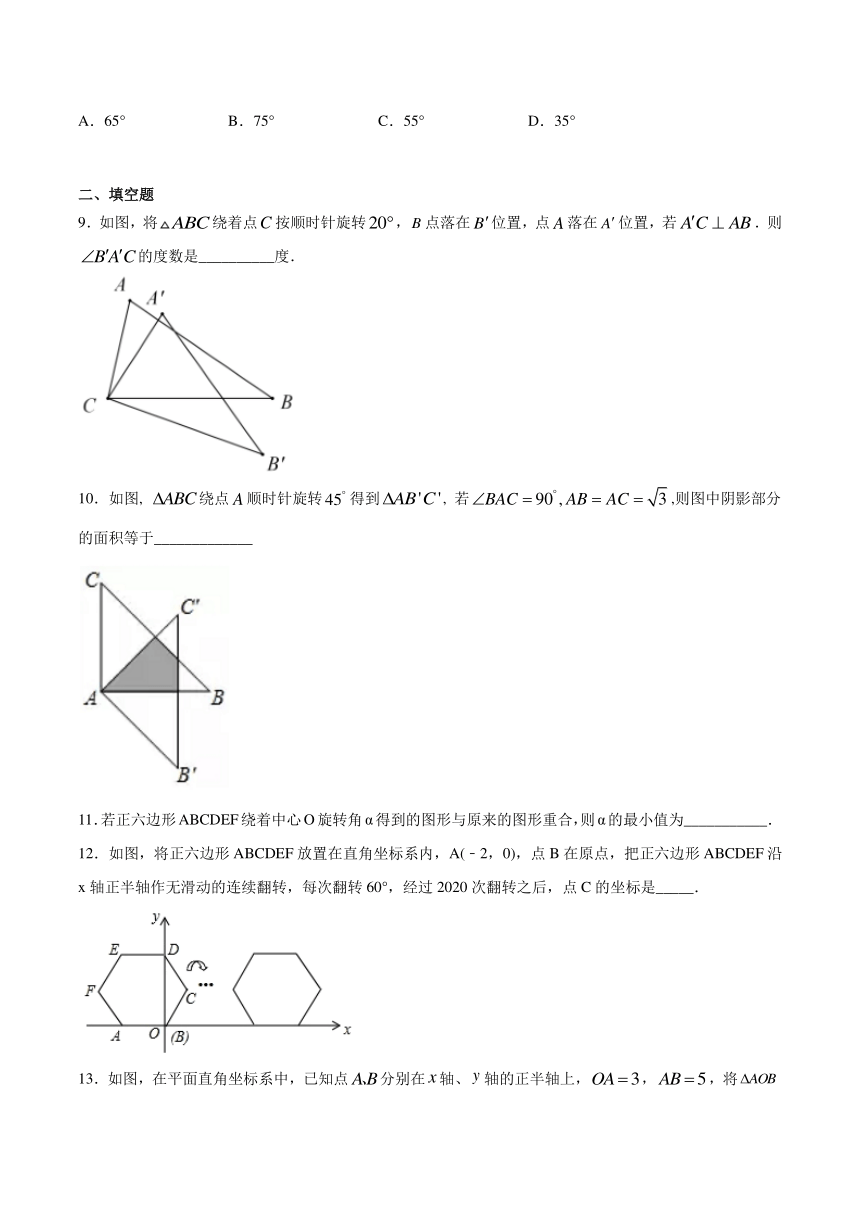
9.如图,将绕着点按顺时针旋转,点落在位置,点落在位置,若.则的度数是__________度.
10.如图, 绕点顺时针旋转得到, 若,则图中阴影部分的面积等于_____________
11.若正六边形ABCDEF绕着中心O旋转角α得到的图形与原来的图形重合,则α的最小值为___________.
12.如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
13.如图,在平面直角坐标系中,已知点分别在轴、轴的正半轴上,,,将绕点按顺时针方向旋转得到,使所在直线经过点,则直线的解析式为__________.
14.如图,是等边三角形内一点,将线段绕点顺时针旋转60°得到线段,连接.若,则四边形的面积为____.
15.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为____________,△ADF是等腰三角形.
16.如图,将边长为的正三角形沿轴正方向作无滑动的连续翻转,点依次落在点的位置,则点的坐标为________.
三、解答题
17.如图,中,,以为边向外作等边,把绕点顺时针方向旋转后到的位置. 若,.
(1)试判断的形状,并说明理由;
(2)求的度数;
(3)求的长.
18.如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3,BC=7,求线段BD的长.
19.如图,在菱形ABCD中,,点E在对角线BD上. 将线段CE绕点C顺时针旋转,得到CF,连接DF.
(1)求证:BE=DF;
(2)连接AC, 若EB=EC ,求证:.
20.如图,在直角坐标系中,边长为的等边的项点都在轴上,顶点在第二象限内,经过平移或轴对称或旋转都可以得到.
(1)沿轴向右平移得到,则平移的距离是 个长度单位;与关于直线对称,则对称轴是 ,绕原点顺时针方向旋转得到,则旋转角度至少是 度;
(2)连接,交于点,求的度数.
21.如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
22.在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
参考答案
1.B2.A3.B4.B5.A6.C7.B8.C
9.70
10.
11.60°
12.(4038,2)
13.
14.24+9.
15.40°或20°.
16.
17.(1)ΔADE 是等边三角形,理由略;(2);(3)AD=7.
18.(1)证明略;(2)5.
19.证明略
20.(1)2,轴,;(2)90°
21.(1)BE=CD;(2)①成立,理由略;②存在,α=45°.
22.(1)点的坐标为;(2)点的坐标为;(3)点的坐标为.
一、单选题
1.下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.在成中心对称的两个图形中,连结对称点的线段都被对称中心平分
C.在平面直角坐标系中,一点向右平移2个单位,纵坐标加2
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
2.如图,在直角坐标系xOy中,△ABC的三个顶点都在方格纸的格点上,点A的坐标是(﹣2,0),将△ABC绕点A顺时针旋转90°得到△AB′C′,则点B的对应点B′的坐标是( )
A.(1,﹣1) B.(1,1) C.(﹣1,1) D.(﹣1,﹣1)
3.王涵将如图1所示的等边三角形绕三条角平分线的交点旋转一定角度后可得到如图2所示的图形,则王涵的旋转方法可以是( )
A.逆时针旋转 B.顺时针旋转 C.逆时针旋转 D.顺时针旋转
4.如图,紫荆花绕自己的旋转中心,按下列角度旋转,不能与其自身重合的是( )
A. B. C. D.
5.一次函数的图象绕着原点逆时针旋转90°后,经过点,则的值为( )
A. B. C. D.1
6.如图,△ABC由△A'B'C'绕0点旋转180°而得到,则下列结论不成立的是( )
A.点A与点A'是对应点
B.BO=B'O
C.∠ACB=∠C'A'B'
D.AB//A'B'
7.如图,两块完全重合的正方形纸片,如果上面的一块绕正方形的中心O逆时针0°~90°的旋转,那么旋转时露出的△ABC的面积(S)随着旋转角度(n)的变化而变化,下面表示S与n关系的图象大致是( )
8.如图,将△ABC绕点C顺时针旋转35°,得△A′B′C,若AC⊥A′B′,则∠BAC=( )
A.65° B.75° C.55° D.35°
二、填空题
9.如图,将绕着点按顺时针旋转,点落在位置,点落在位置,若.则的度数是__________度.
10.如图, 绕点顺时针旋转得到, 若,则图中阴影部分的面积等于_____________
11.若正六边形ABCDEF绕着中心O旋转角α得到的图形与原来的图形重合,则α的最小值为___________.
12.如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
13.如图,在平面直角坐标系中,已知点分别在轴、轴的正半轴上,,,将绕点按顺时针方向旋转得到,使所在直线经过点,则直线的解析式为__________.
14.如图,是等边三角形内一点,将线段绕点顺时针旋转60°得到线段,连接.若,则四边形的面积为____.
15.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为____________,△ADF是等腰三角形.
16.如图,将边长为的正三角形沿轴正方向作无滑动的连续翻转,点依次落在点的位置,则点的坐标为________.
三、解答题
17.如图,中,,以为边向外作等边,把绕点顺时针方向旋转后到的位置. 若,.
(1)试判断的形状,并说明理由;
(2)求的度数;
(3)求的长.
18.如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3,BC=7,求线段BD的长.
19.如图,在菱形ABCD中,,点E在对角线BD上. 将线段CE绕点C顺时针旋转,得到CF,连接DF.
(1)求证:BE=DF;
(2)连接AC, 若EB=EC ,求证:.
20.如图,在直角坐标系中,边长为的等边的项点都在轴上,顶点在第二象限内,经过平移或轴对称或旋转都可以得到.
(1)沿轴向右平移得到,则平移的距离是 个长度单位;与关于直线对称,则对称轴是 ,绕原点顺时针方向旋转得到,则旋转角度至少是 度;
(2)连接,交于点,求的度数.
21.如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
22.在平面直角坐标系中,四边形是矩形,点,点,点.以点为中心,顺时针旋转矩形,得到矩形,点的对应点分别为,记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在的延长线上时,求点的坐标;
(3)当点落在线段上时,求点的坐标(直接写出结果即可).
参考答案
1.B2.A3.B4.B5.A6.C7.B8.C
9.70
10.
11.60°
12.(4038,2)
13.
14.24+9.
15.40°或20°.
16.
17.(1)ΔADE 是等边三角形,理由略;(2);(3)AD=7.
18.(1)证明略;(2)5.
19.证明略
20.(1)2,轴,;(2)90°
21.(1)BE=CD;(2)①成立,理由略;②存在,α=45°.
22.(1)点的坐标为;(2)点的坐标为;(3)点的坐标为.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
