人教版数学八年级下册数学17.1:勾股定理 同步练习(解析版)
文档属性
| 名称 | 人教版数学八年级下册数学17.1:勾股定理 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 326.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 08:50:49 | ||
图片预览

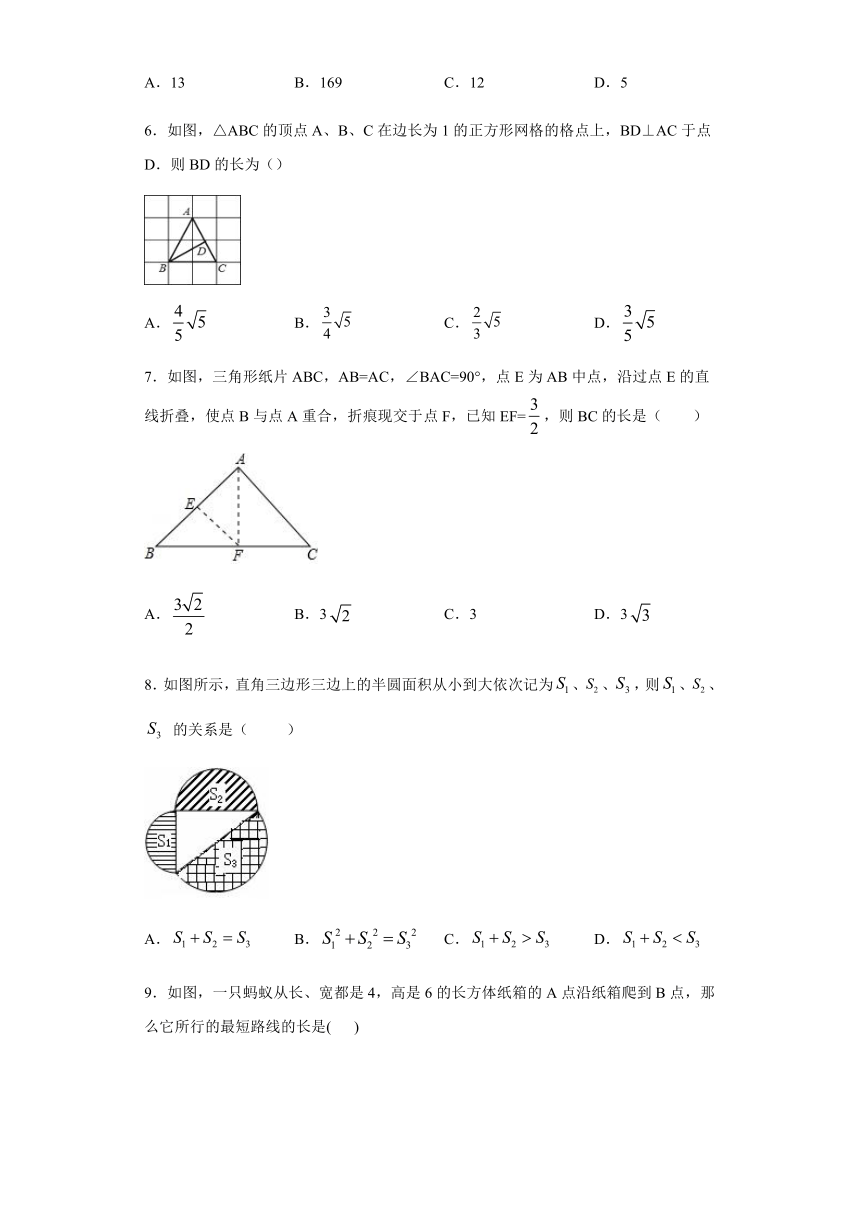
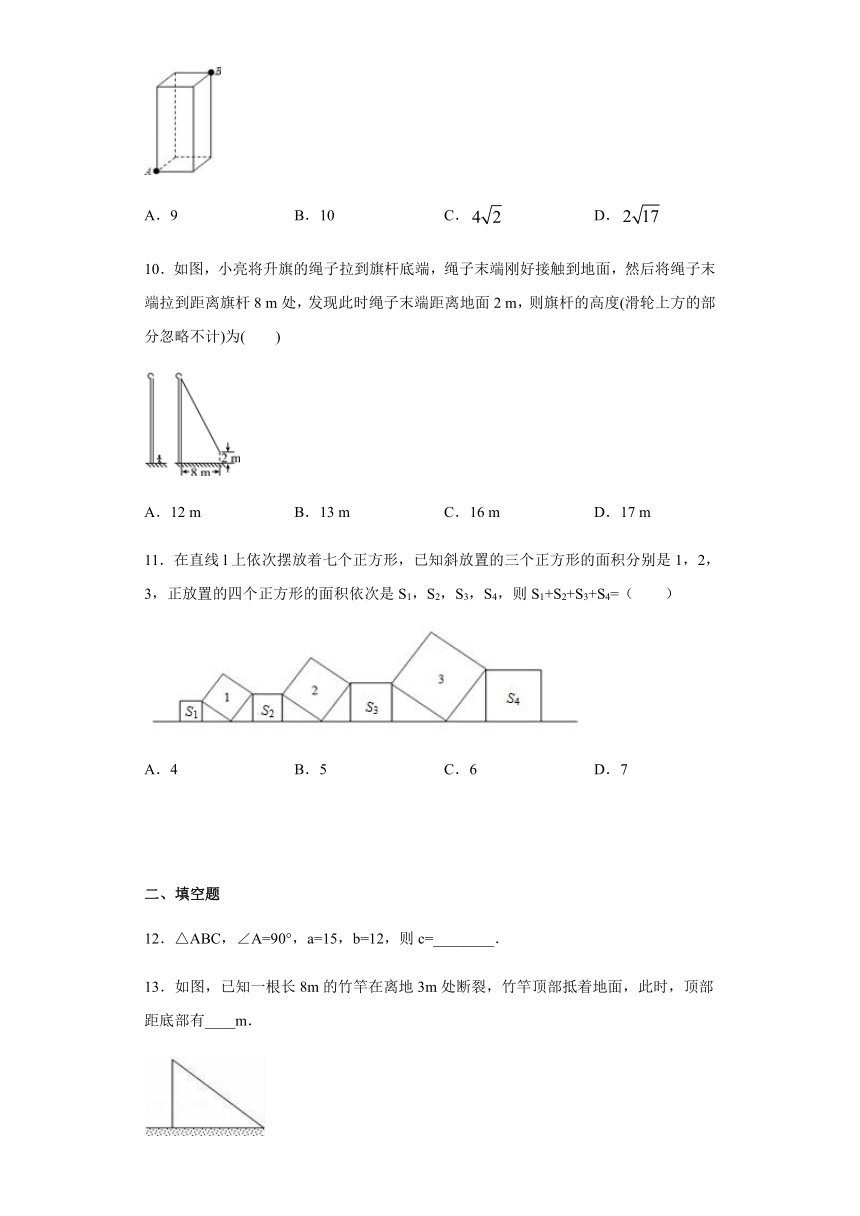
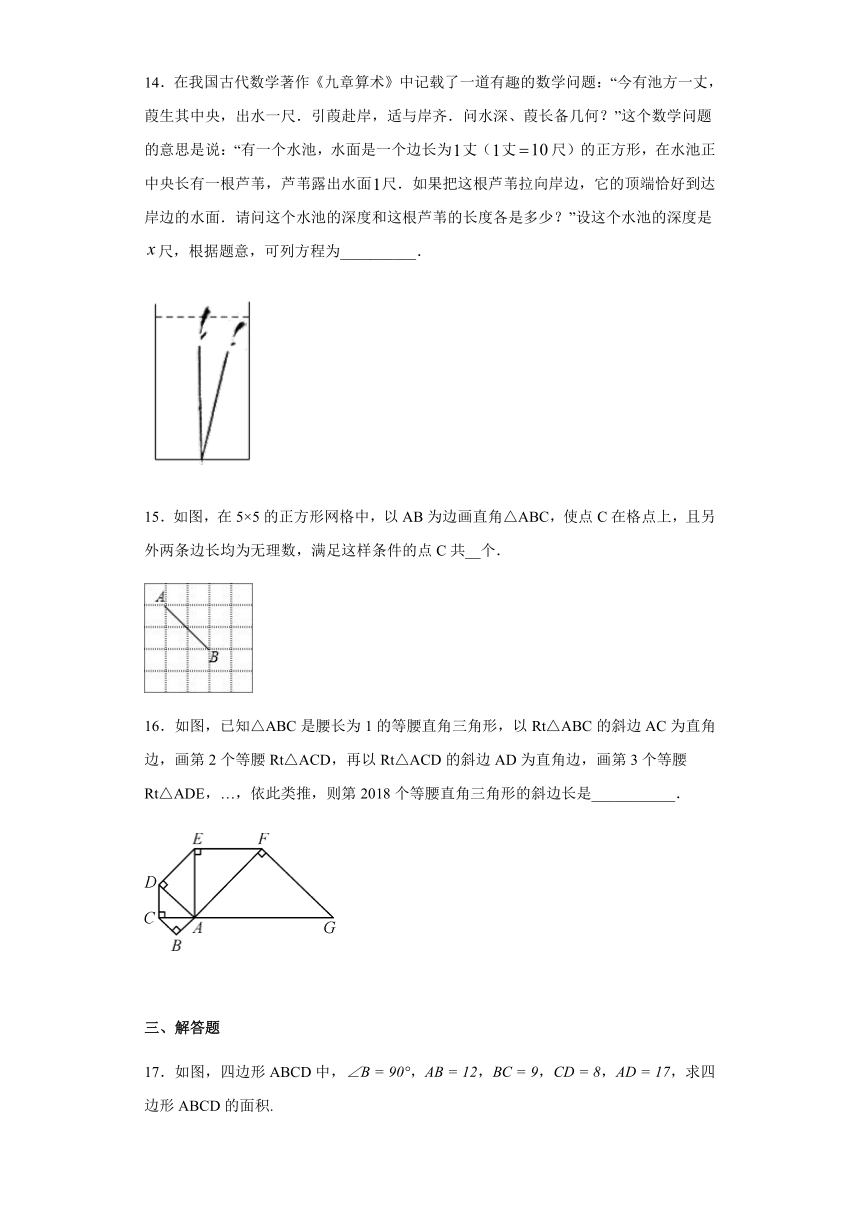

文档简介
人教版八年级下册数学试题:17.1勾股定理 同步练习
一、单选题
1.已知直角三角形的两条直角边的长分别是1,,则斜边长为( )
A.1 B. C.2 D.3
2.下面各图中,不能证明勾股定理正确性的是( )
A. B. C. D.
3.一直角三角形的三边分别为2、3、x,那么x为( )
A. B. C.或 D.无法确定
4.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
5.如图,在中,,正方形的面积分别为25和144,则的长度为( )
A.13 B.169 C.12 D.5
6.如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD的长为()
A. B. C. D.
7.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
8.如图所示,直角三边形三边上的半圆面积从小到大依次记为、、,则、、 的关系是( )
A. B. C. D.
9.如图,一只蚂蚁从长、宽都是4,高是6的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
A.9 B.10 C. D.
10.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m C.16 m D.17 m
11.在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=( )
A.4 B.5 C.6 D.7
二、填空题
12.△ABC,∠A=90°,a=15,b=12,则c=________.
13.如图,已知一根长8m的竹竿在离地3m处断裂,竹竿顶部抵着地面,此时,顶部距底部有____m.
14.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长备几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为丈(丈尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是尺,根据题意,可列方程为__________.
15.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样条件的点C共__个.
16.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第2个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是___________.
三、解答题
17.如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
18.如图,三个村庄A,B,C之间的距离分别为km, km, km.要从B修一条公路直达AC,已知公路的造价为26000元/km,修这条公路的最低造价是多少?
19.“中华人民共和国道路交通管理条例”规定,小汽车在设有中心双实线、中心分隔带、机动车道与非机动车道分隔设施的城市街道上的行驶速度不得超过70千米/时.如图,一辆“小汽车”在一条城市道路上沿直线行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米的C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由
20.如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.
21.设,,.
(1)当x取什么实数时,a,b,c都有意义;
(2)若Rt△ABC三条边的长分别为a,b,c,求x的值.
参考答案
1.C
【解析】
解:直角三角形的两条直角边的长分别为1,,
则斜边长==2;
故选C.
2.C
【解析】
解:A、∵+c2+ab=(a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4× +(b﹣a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、根据图形不能证明勾股定理,故本选项符合题意;
D、∵4× +c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
故选C.
3.C
【解析】
解:当3为斜边时,
32=22+x2,解得:x=,
当x为斜边时,
x2=32+22,解得:x=,
∴x为或,
故选C.
4.A
【解析】
根据题意可得BC=4cm,CD=3cm,根据Rt△BCD的勾股定理可得BD=5cm,则AD=BD=5cm,所以橡皮筋被拉长了(5+5)-8=2cm.
5.A
【解析】
解:∵在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
又∵AC2=144,BC2=25,
∴AB2=25+144=169,
∴AB==13.
故选:A.
6.A
【解析】
如图,
△ABC的面积=×BC×AE=2,
由勾股定理得,AC=,
则××BD=2,
解得BD=,
故选A.
7.B
【解析】
解:
AB=AC,
,
故选B.
8.A
【解析】
解:设三个半圆的直径分别为:d1、d2、d3,
S1=×π×()2=,
S2=×π×()2=,
S3=×π×()2=.
由勾股定理可得:
d12+d22=d32,
∴S1+S2=(d12+d22)==S3,
所以S1、S2、S3的关系是:S1+S2=S3.
故选A.
9.B
【解析】
如图(1),AB=;
如图(2),AB=.
故选B.
10.D
【解析】
设旗杆高度为x,则AC=AD=x,AB=(x﹣2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x﹣2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选D.
11.A
【解析】
解:由勾股定理的几何意义可知:S1+S2=1,S2+S3=2,S3+S4=3,S1+S2+S3+S4=4,故选A.
12.9
【解析】
c=故答案为9.
13.4
【解析】
解如图所示:在RtABC中,BC=3,AC=5,
由勾股定理可得:AB2+BC2=AC2
设旗杆顶部距离底部AB=x米,则有32+x2=52,
解得x=4
故答案为:4.
14.
【解析】
设由题意可得:.故答案为.
15.4
【解析】
解:根据题意可得以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 8个.
故答案为8.
16.()2018
【解析】
解:∵△ABC是腰长为1的等腰直角三形,
∴△ABC的斜边长是,
第2个等腰直角三角形的斜边长是:×=()2,
第3个等腰直角三角形的斜边长是:()2×=()3,
…,
∴第2012个等腰直角三角形的斜边长是()2018.
故答案为()2018.
17.114
【解析】
解:如图所示,连接AC,
∵,
∴,
∵,,
∴,
∴,
∴.
18.修这条公路的最低造价是12万元.
【解析】
解:∵BC2+AB2=122+52=169,AC2=132=169,
∴BC2+AB2=AC2,
∴∠ABC=90°,当BD⊥AC时BD最短,造价最低,
∵S△ABC=AB?BC=AC?BD,
∴,
×2600=12000(万元),
答:最低造价为12000万元.
19.这辆“小汽车”超速了.
【解析】
解:这辆“小汽车”超速了,理由:
由题意知,米,米,且为直角三角形,AB是斜边,
根据勾股定理,得,
可以求得:米千米,6秒时,
所以速度为小车此时速度为千米/时,
所以这辆“小汽车”超速了.
20.(1)BD=1m;(2)CE与BE的大小关系是CE=BE,证明见解析.
【解析】
(1)∵AO⊥OD,AO=4m,AB=5m,
∴OB==3m,
∵梯子的顶端A沿墙下滑1m至C点,
∴OC=AO﹣AC=3m,
∵CD=AB=5m,
∴由勾股定理得:OD=4m,
∴BD=OD﹣OB=4m﹣3m=1m;
(2)CE与BE的大小关系是CE=BE,证明如下:
连接CB,由(1)知:AO=DO=4m,AB=CD=5m,
∵∠AOB=∠DOC=90°,
在Rt△AOB和Rt△DOC中
,
∴Rt△AOB≌Rt△DOC(HL),
∴∠ABO=∠DCO,OC=OB,
∴∠OCB=∠OBC,
∴∠ABO﹣∠OBC=∠DCO﹣∠OCB,
∴∠EBC=∠ECB,
∴CE=BE.
21.(1);(2)x=或2.
【解析】
解:(1)由二次根式的性质,得 ,
解得;
(2)当c为斜边时,由a2+b2=c2,
即8-x+3x+4=x+2,
解得x=-10,
当b为斜边时,a2+c2=b2,
即8-x+x+2=3x+4,
解得x=2,
当a为斜边时,b2+c2=a2,
即3x+4+x+2=8-x,
解得x=
∵
∴x=或2.
一、单选题
1.已知直角三角形的两条直角边的长分别是1,,则斜边长为( )
A.1 B. C.2 D.3
2.下面各图中,不能证明勾股定理正确性的是( )
A. B. C. D.
3.一直角三角形的三边分别为2、3、x,那么x为( )
A. B. C.或 D.无法确定
4.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
A.2cm B.3cm C.4cm D.5cm
5.如图,在中,,正方形的面积分别为25和144,则的长度为( )
A.13 B.169 C.12 D.5
6.如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD的长为()
A. B. C. D.
7.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=,则BC的长是( )
A. B.3 C.3 D.3
8.如图所示,直角三边形三边上的半圆面积从小到大依次记为、、,则、、 的关系是( )
A. B. C. D.
9.如图,一只蚂蚁从长、宽都是4,高是6的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
A.9 B.10 C. D.
10.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12 m B.13 m C.16 m D.17 m
11.在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=( )
A.4 B.5 C.6 D.7
二、填空题
12.△ABC,∠A=90°,a=15,b=12,则c=________.
13.如图,已知一根长8m的竹竿在离地3m处断裂,竹竿顶部抵着地面,此时,顶部距底部有____m.
14.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长备几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为丈(丈尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是尺,根据题意,可列方程为__________.
15.如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,且另外两条边长均为无理数,满足这样条件的点C共__个.
16.如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第2个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第3个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是___________.
三、解答题
17.如图,四边形ABCD中,,,,,,求四边形ABCD的面积.
18.如图,三个村庄A,B,C之间的距离分别为km, km, km.要从B修一条公路直达AC,已知公路的造价为26000元/km,修这条公路的最低造价是多少?
19.“中华人民共和国道路交通管理条例”规定,小汽车在设有中心双实线、中心分隔带、机动车道与非机动车道分隔设施的城市街道上的行驶速度不得超过70千米/时.如图,一辆“小汽车”在一条城市道路上沿直线行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米的C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由
20.如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.
21.设,,.
(1)当x取什么实数时,a,b,c都有意义;
(2)若Rt△ABC三条边的长分别为a,b,c,求x的值.
参考答案
1.C
【解析】
解:直角三角形的两条直角边的长分别为1,,
则斜边长==2;
故选C.
2.C
【解析】
解:A、∵+c2+ab=(a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4× +(b﹣a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、根据图形不能证明勾股定理,故本选项符合题意;
D、∵4× +c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
故选C.
3.C
【解析】
解:当3为斜边时,
32=22+x2,解得:x=,
当x为斜边时,
x2=32+22,解得:x=,
∴x为或,
故选C.
4.A
【解析】
根据题意可得BC=4cm,CD=3cm,根据Rt△BCD的勾股定理可得BD=5cm,则AD=BD=5cm,所以橡皮筋被拉长了(5+5)-8=2cm.
5.A
【解析】
解:∵在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
又∵AC2=144,BC2=25,
∴AB2=25+144=169,
∴AB==13.
故选:A.
6.A
【解析】
如图,
△ABC的面积=×BC×AE=2,
由勾股定理得,AC=,
则××BD=2,
解得BD=,
故选A.
7.B
【解析】
解:
AB=AC,
,
故选B.
8.A
【解析】
解:设三个半圆的直径分别为:d1、d2、d3,
S1=×π×()2=,
S2=×π×()2=,
S3=×π×()2=.
由勾股定理可得:
d12+d22=d32,
∴S1+S2=(d12+d22)==S3,
所以S1、S2、S3的关系是:S1+S2=S3.
故选A.
9.B
【解析】
如图(1),AB=;
如图(2),AB=.
故选B.
10.D
【解析】
设旗杆高度为x,则AC=AD=x,AB=(x﹣2)m,BC=8m,
在Rt△ABC中,AB2+BC2=AC2,即(x﹣2)2+82=x2,
解得:x=17,
即旗杆的高度为17米.
故选D.
11.A
【解析】
解:由勾股定理的几何意义可知:S1+S2=1,S2+S3=2,S3+S4=3,S1+S2+S3+S4=4,故选A.
12.9
【解析】
c=故答案为9.
13.4
【解析】
解如图所示:在RtABC中,BC=3,AC=5,
由勾股定理可得:AB2+BC2=AC2
设旗杆顶部距离底部AB=x米,则有32+x2=52,
解得x=4
故答案为:4.
14.
【解析】
设由题意可得:.故答案为.
15.4
【解析】
解:根据题意可得以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C共 8个.
故答案为8.
16.()2018
【解析】
解:∵△ABC是腰长为1的等腰直角三形,
∴△ABC的斜边长是,
第2个等腰直角三角形的斜边长是:×=()2,
第3个等腰直角三角形的斜边长是:()2×=()3,
…,
∴第2012个等腰直角三角形的斜边长是()2018.
故答案为()2018.
17.114
【解析】
解:如图所示,连接AC,
∵,
∴,
∵,,
∴,
∴,
∴.
18.修这条公路的最低造价是12万元.
【解析】
解:∵BC2+AB2=122+52=169,AC2=132=169,
∴BC2+AB2=AC2,
∴∠ABC=90°,当BD⊥AC时BD最短,造价最低,
∵S△ABC=AB?BC=AC?BD,
∴,
×2600=12000(万元),
答:最低造价为12000万元.
19.这辆“小汽车”超速了.
【解析】
解:这辆“小汽车”超速了,理由:
由题意知,米,米,且为直角三角形,AB是斜边,
根据勾股定理,得,
可以求得:米千米,6秒时,
所以速度为小车此时速度为千米/时,
所以这辆“小汽车”超速了.
20.(1)BD=1m;(2)CE与BE的大小关系是CE=BE,证明见解析.
【解析】
(1)∵AO⊥OD,AO=4m,AB=5m,
∴OB==3m,
∵梯子的顶端A沿墙下滑1m至C点,
∴OC=AO﹣AC=3m,
∵CD=AB=5m,
∴由勾股定理得:OD=4m,
∴BD=OD﹣OB=4m﹣3m=1m;
(2)CE与BE的大小关系是CE=BE,证明如下:
连接CB,由(1)知:AO=DO=4m,AB=CD=5m,
∵∠AOB=∠DOC=90°,
在Rt△AOB和Rt△DOC中
,
∴Rt△AOB≌Rt△DOC(HL),
∴∠ABO=∠DCO,OC=OB,
∴∠OCB=∠OBC,
∴∠ABO﹣∠OBC=∠DCO﹣∠OCB,
∴∠EBC=∠ECB,
∴CE=BE.
21.(1);(2)x=或2.
【解析】
解:(1)由二次根式的性质,得 ,
解得;
(2)当c为斜边时,由a2+b2=c2,
即8-x+3x+4=x+2,
解得x=-10,
当b为斜边时,a2+c2=b2,
即8-x+x+2=3x+4,
解得x=2,
当a为斜边时,b2+c2=a2,
即3x+4+x+2=8-x,
解得x=
∵
∴x=或2.
