六年级数学下册提升课件-第4单元 圆柱和圆锥-冀教版(共44张PPT)
文档属性
| 名称 | 六年级数学下册提升课件-第4单元 圆柱和圆锥-冀教版(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 10:59:11 | ||
图片预览







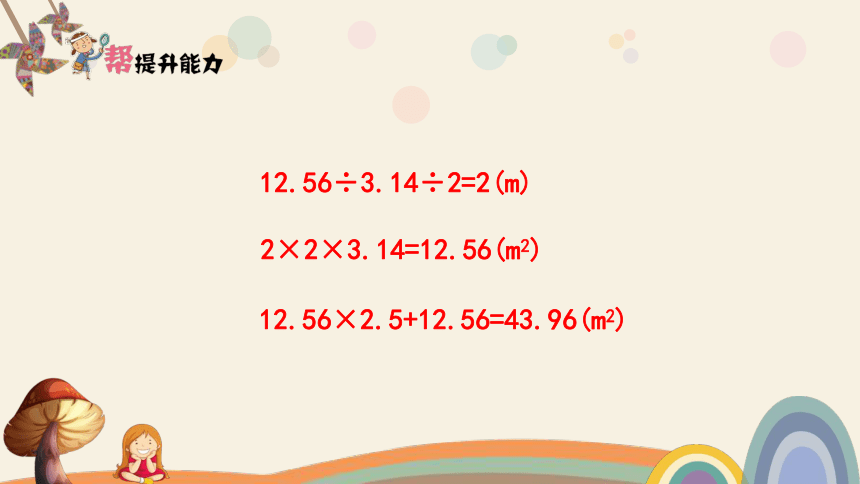



文档简介
(共44张PPT)
提升拓展课件
冀教版六年级下
第1课时 圆柱及其侧面积
圆柱的侧面积与圆柱的关系
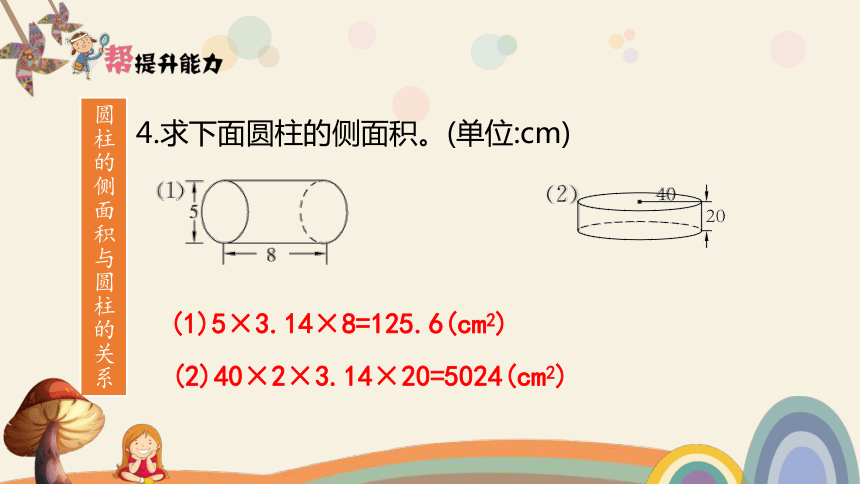
4.求下面圆柱的侧面积。(单位:cm)
(1)5×3.14×8=125.6(cm2)
(2)40×2×3.14×20=5024(cm2)
运用圆柱侧面积的知识
解决复杂问题
5.某博物馆的展厅内有10根相同的圆柱形柱子支撑展厅的顶棚。每根柱子的底面周长是1.256米,高是6米。如果每平方米用油漆1.6千克,那么粉刷这些柱子需要油漆多少千克?
1.256×6=7.536(平方米)
7.536×1.6=12.0576(千克)
12.0576×10=120.576(千克)
第2课时 圆柱的表面积 (1)
巧求圆柱的表面积
5.一张长方形纸板,剪下两个圆和一个长方形后,正好可以做成一个圆柱,这个圆柱的底面半径为10 cm,那么原来的长方形纸板的面积是多少平方厘米?
(2×3.14×10+10×2×2)×(10×2)=2056(cm2)
第3课时 圆柱的表面积(2)
复杂的表面积问题
3.河北省地热资源丰富,有很多温泉度假村。一温泉度假村新建了一个圆柱形温泉池,水池内部的底面周长是12.56 m,深是2.5 m,这个水池的占地面积是多少?现在要在水池的内壁和底部贴瓷砖,贴瓷砖的面积是多少?
12.56÷3.14÷2=2(m)
2×2×3.14=12.56(m2)
12.56×2.5+12.56=43.96(m2)
4.如图所示,一个蔬菜大棚的外形是半圆柱形。两端是半径为3米高的半圆形,长为100米。求覆盖的塑料薄膜至少需要多少平方米。
3×3×3.14=28.26(平方米)
2×3×3.14×100÷2=942(平方米)
942+28.26=970.26(平方米)
第4课时 圆柱的体积(1)
从“面动成体”的角度
求圆柱的体积
5.把一个长10 cm,宽4 cm的长方形以长边所在直线为轴旋转一周,得到的圆柱的体积是多少立方厘米?
42×3.14×10=502.4(cm3)
第5课时 圆柱的体积(2)
圆柱体体积的应用
2.一个圆柱形水池,底面直径是30米,深3米。
(1)这个水池的占地面积是多少?
(2)挖这个水池,共需挖土多少立方米?
3.14×(30÷2)2=706.5(平方米)
706.5×3=2119.5(立方米)
3.浩浩要用一张长18.84 cm,宽12.56 cm的长方形纸围成一个圆柱,怎样围体积最大?
(1)用长方形的长作为圆柱的底面周长,围成的圆柱体积是多少?
18.84÷3.14÷2=3(cm)
3.14×32×12.56=354.9456
(2)用长方形的宽作为圆柱的底面周长,围成的圆柱体积是多少?
?
?
我发现:用同一张纸围成的“粗而短”的圆柱体积( ),“细而长”的圆柱体积( )。
12.56÷3.14÷2=2(cm)
大
3.14×22×18.84=236.6304(cm3)
小
通过圆柱的体积求高
4.一社区在小区的健身广场新建了一个圆柱形水池,如果要注满,需要84.78 m3的水。水池的底面积是28.26 m2,深是多少米?
84.78÷28.26=3(m)
第6课时 测量体积
复杂的圆柱体积问题
2.一个圆柱形油桶,底面周长为12.56分米,高是1.5米。如果每立方米柴油重0.7吨,这个油桶能装多少吨柴油?
12.56÷3.14÷2=2(分米)
2分米=0.2米
0.2×0.2×3.14×1.5=0.1884(立方米)
0.1884×0.7=0.13188(吨)
3.把一根长4 m的圆柱形木头截成3段小圆柱形木头,表面积增加96 dm2,则原来的圆柱形木头的体积是多少?
96÷(3-1)÷2=24(dm2)
24 dm2=0.24 m2
0.24×4=0.96(m3)
4.一卷卫生纸,内直径是4厘米,外直径是10厘米,高是10厘米,这卷卫生纸的体积是多少立方厘米?
[(10÷2)2-(4÷2)2]×3.14×10
=659.4(立方厘米)
5.把一个底面半径是10厘米,高是3厘米的圆柱形钢材,熔铸成一个底面积是50平方厘米的长方体,长方体的高是多少厘米?
102×3.14×3÷50=18.84(厘米)
第7课时 计算容积
通过圆柱的容积求高
5.一个圆柱形水桶的容积是80升,里面装了60%的水,已知它的底面积是10平方分米,桶里水面的高度是多少分米?
80×60%=48(升)=48(立方分米)
48÷10=4.8(分米)
体积、容积转化成质量
6.如图所示,一个圆柱形蓄水池,从里面量,底面直径是20米,高是5米。这个蓄水池的容积是多少?如果将这个蓄水池里注满水,水重多少吨?(1立方米的水重1吨)
(20÷2)2×3.14×5
=1570(立方米)
1570×1=1570(吨)
第8课时 饮水问题
用转化思想解决体积
与容积之间的问题
2.如图所示,这个杯子能装下300毫升牛奶吗?
(不考虑杯壁的厚度)
(8÷2)2×3.14×10=502.4(cm3)
502.4 cm3=502.4毫升
502.4>300
能
3.如图所示,甲桶能装下乙桶里的水吗?
甲桶:3.14×( )2×5=251.2(立方分米)
8
2
乙桶:3.14×( )2×10=125.6(立方分米)
4
2
251.2>125.6
能装下
4.子涵有一个圆柱形的水杯,从里面量,水杯的底面半径是4厘米,高是10厘米。
(1)这个水杯的容积是多少毫升?
3.14×42×10=502.4(立方厘米)=502.4(毫升)
(2)有关资料显示:每人每天的正常饮水量大约是1.8升。小刚一天要喝几杯水?(得数保留整数)
?
?
(3)一桶16升的矿泉水大约可以盛多少杯水?(得数保留整数)
1.8升=1800毫升
16升=16000毫升
1800÷502.4≈4(杯)
16000÷502.4≈32(杯)
第9课时 不规则物体体积的测量
复杂问题
5.笑松把一个高为15厘米,容积为300毫升的圆柱形容器里装满了水,当把一个长为5厘米、宽为4厘米、高为3厘米的长方体铅块浸入水中后,容器中有一部分水溢出,当把铅块取出后,容器中水有多高?
300毫升=300立方厘米
容器的底面积:300÷15=20(平方厘米)
铅块的体积:5×4×3=60(立方厘米)
取出铅块后,容器中水下降的高度:60÷20=3(厘米)
取出铅块后,容器中水的高度:15-3=12(厘米)
6.一个棱长10厘米的正方体容器,里面装的水深5.5厘米,如果把一个底面半径为2厘米,高为3厘米的圆柱形零件浸没水中(水没有溢出),水面将上升多少厘米?
22×3.14×3=37.68(立方厘米)
37.68÷(10×10)=0.3768(厘米)
7.一枚5角钱硬币的体积非常小,你能设计出一个方法知道它的体积大约是多少吗?
可以将多枚硬币放入装有部分水的容器中,让水面上升的高度可以测量出来,计算出上升的水的体积再除以硬币的数量。
第10课时 圆锥和圆锥的体积公式
运用等积变形的思想解决
与体积有关的问题
6.将一个底面半径为20 cm,高为27 cm的圆锥形铁坯铸成一个底面半径为15 cm的圆柱形铁坯,圆柱形铁坯的高是多少?
202×3.14×27× =11304(cm3)
11304÷(152×3.14)=16(cm)
1
3
第11课时 圆锥的体积
从“面动成体”的角度
进一步认识圆锥
4.将右图中的直角三角形以8 cm 的直角边所在直线为轴旋转一周,可以得到一个( ),这个图形的高是( )cm,底面直径是
( )cm。这个图形的体积是多少?
圆锥
8
12
62×3.14×8÷3=301.44(cm3)
求高问题
5.一个圆柱体底面积是5平方分米,把它削成一个最大的圆锥,削去部分的体积是6立方分米,求这个圆柱的高是多少?
6÷(1- )=9(立方分米)
1
3
9÷5=1.8(分米)
木材加工问题
将圆木加工成最大的方木
2.将一根圆木(如下图)加工成最大的方木。
(1)方木的体积是多少立方米?
16 cm=0.16 m
0.16×(0.16+0.16)÷2×2=0.0512(m2)
0.0512×5=0.256(m3)
(2)废木料大约有多少立方米?(得数保留两位小数)
?
?
(3)几根方木的体积约是1立方米?
0.162×3.14×5-0.256≈0.15(m3)
1÷0.256≈4(根)
谢谢观赏
谢谢观赏
谢谢观赏
提升拓展课件
冀教版六年级下
第1课时 圆柱及其侧面积
圆柱的侧面积与圆柱的关系
4.求下面圆柱的侧面积。(单位:cm)
(1)5×3.14×8=125.6(cm2)
(2)40×2×3.14×20=5024(cm2)
运用圆柱侧面积的知识
解决复杂问题
5.某博物馆的展厅内有10根相同的圆柱形柱子支撑展厅的顶棚。每根柱子的底面周长是1.256米,高是6米。如果每平方米用油漆1.6千克,那么粉刷这些柱子需要油漆多少千克?
1.256×6=7.536(平方米)
7.536×1.6=12.0576(千克)
12.0576×10=120.576(千克)
第2课时 圆柱的表面积 (1)
巧求圆柱的表面积
5.一张长方形纸板,剪下两个圆和一个长方形后,正好可以做成一个圆柱,这个圆柱的底面半径为10 cm,那么原来的长方形纸板的面积是多少平方厘米?
(2×3.14×10+10×2×2)×(10×2)=2056(cm2)
第3课时 圆柱的表面积(2)
复杂的表面积问题
3.河北省地热资源丰富,有很多温泉度假村。一温泉度假村新建了一个圆柱形温泉池,水池内部的底面周长是12.56 m,深是2.5 m,这个水池的占地面积是多少?现在要在水池的内壁和底部贴瓷砖,贴瓷砖的面积是多少?
12.56÷3.14÷2=2(m)
2×2×3.14=12.56(m2)
12.56×2.5+12.56=43.96(m2)
4.如图所示,一个蔬菜大棚的外形是半圆柱形。两端是半径为3米高的半圆形,长为100米。求覆盖的塑料薄膜至少需要多少平方米。
3×3×3.14=28.26(平方米)
2×3×3.14×100÷2=942(平方米)
942+28.26=970.26(平方米)
第4课时 圆柱的体积(1)
从“面动成体”的角度
求圆柱的体积
5.把一个长10 cm,宽4 cm的长方形以长边所在直线为轴旋转一周,得到的圆柱的体积是多少立方厘米?
42×3.14×10=502.4(cm3)
第5课时 圆柱的体积(2)
圆柱体体积的应用
2.一个圆柱形水池,底面直径是30米,深3米。
(1)这个水池的占地面积是多少?
(2)挖这个水池,共需挖土多少立方米?
3.14×(30÷2)2=706.5(平方米)
706.5×3=2119.5(立方米)
3.浩浩要用一张长18.84 cm,宽12.56 cm的长方形纸围成一个圆柱,怎样围体积最大?
(1)用长方形的长作为圆柱的底面周长,围成的圆柱体积是多少?
18.84÷3.14÷2=3(cm)
3.14×32×12.56=354.9456
(2)用长方形的宽作为圆柱的底面周长,围成的圆柱体积是多少?
?
?
我发现:用同一张纸围成的“粗而短”的圆柱体积( ),“细而长”的圆柱体积( )。
12.56÷3.14÷2=2(cm)
大
3.14×22×18.84=236.6304(cm3)
小
通过圆柱的体积求高
4.一社区在小区的健身广场新建了一个圆柱形水池,如果要注满,需要84.78 m3的水。水池的底面积是28.26 m2,深是多少米?
84.78÷28.26=3(m)
第6课时 测量体积
复杂的圆柱体积问题
2.一个圆柱形油桶,底面周长为12.56分米,高是1.5米。如果每立方米柴油重0.7吨,这个油桶能装多少吨柴油?
12.56÷3.14÷2=2(分米)
2分米=0.2米
0.2×0.2×3.14×1.5=0.1884(立方米)
0.1884×0.7=0.13188(吨)
3.把一根长4 m的圆柱形木头截成3段小圆柱形木头,表面积增加96 dm2,则原来的圆柱形木头的体积是多少?
96÷(3-1)÷2=24(dm2)
24 dm2=0.24 m2
0.24×4=0.96(m3)
4.一卷卫生纸,内直径是4厘米,外直径是10厘米,高是10厘米,这卷卫生纸的体积是多少立方厘米?
[(10÷2)2-(4÷2)2]×3.14×10
=659.4(立方厘米)
5.把一个底面半径是10厘米,高是3厘米的圆柱形钢材,熔铸成一个底面积是50平方厘米的长方体,长方体的高是多少厘米?
102×3.14×3÷50=18.84(厘米)
第7课时 计算容积
通过圆柱的容积求高
5.一个圆柱形水桶的容积是80升,里面装了60%的水,已知它的底面积是10平方分米,桶里水面的高度是多少分米?
80×60%=48(升)=48(立方分米)
48÷10=4.8(分米)
体积、容积转化成质量
6.如图所示,一个圆柱形蓄水池,从里面量,底面直径是20米,高是5米。这个蓄水池的容积是多少?如果将这个蓄水池里注满水,水重多少吨?(1立方米的水重1吨)
(20÷2)2×3.14×5
=1570(立方米)
1570×1=1570(吨)
第8课时 饮水问题
用转化思想解决体积
与容积之间的问题
2.如图所示,这个杯子能装下300毫升牛奶吗?
(不考虑杯壁的厚度)
(8÷2)2×3.14×10=502.4(cm3)
502.4 cm3=502.4毫升
502.4>300
能
3.如图所示,甲桶能装下乙桶里的水吗?
甲桶:3.14×( )2×5=251.2(立方分米)
8
2
乙桶:3.14×( )2×10=125.6(立方分米)
4
2
251.2>125.6
能装下
4.子涵有一个圆柱形的水杯,从里面量,水杯的底面半径是4厘米,高是10厘米。
(1)这个水杯的容积是多少毫升?
3.14×42×10=502.4(立方厘米)=502.4(毫升)
(2)有关资料显示:每人每天的正常饮水量大约是1.8升。小刚一天要喝几杯水?(得数保留整数)
?
?
(3)一桶16升的矿泉水大约可以盛多少杯水?(得数保留整数)
1.8升=1800毫升
16升=16000毫升
1800÷502.4≈4(杯)
16000÷502.4≈32(杯)
第9课时 不规则物体体积的测量
复杂问题
5.笑松把一个高为15厘米,容积为300毫升的圆柱形容器里装满了水,当把一个长为5厘米、宽为4厘米、高为3厘米的长方体铅块浸入水中后,容器中有一部分水溢出,当把铅块取出后,容器中水有多高?
300毫升=300立方厘米
容器的底面积:300÷15=20(平方厘米)
铅块的体积:5×4×3=60(立方厘米)
取出铅块后,容器中水下降的高度:60÷20=3(厘米)
取出铅块后,容器中水的高度:15-3=12(厘米)
6.一个棱长10厘米的正方体容器,里面装的水深5.5厘米,如果把一个底面半径为2厘米,高为3厘米的圆柱形零件浸没水中(水没有溢出),水面将上升多少厘米?
22×3.14×3=37.68(立方厘米)
37.68÷(10×10)=0.3768(厘米)
7.一枚5角钱硬币的体积非常小,你能设计出一个方法知道它的体积大约是多少吗?
可以将多枚硬币放入装有部分水的容器中,让水面上升的高度可以测量出来,计算出上升的水的体积再除以硬币的数量。
第10课时 圆锥和圆锥的体积公式
运用等积变形的思想解决
与体积有关的问题
6.将一个底面半径为20 cm,高为27 cm的圆锥形铁坯铸成一个底面半径为15 cm的圆柱形铁坯,圆柱形铁坯的高是多少?
202×3.14×27× =11304(cm3)
11304÷(152×3.14)=16(cm)
1
3
第11课时 圆锥的体积
从“面动成体”的角度
进一步认识圆锥
4.将右图中的直角三角形以8 cm 的直角边所在直线为轴旋转一周,可以得到一个( ),这个图形的高是( )cm,底面直径是
( )cm。这个图形的体积是多少?
圆锥
8
12
62×3.14×8÷3=301.44(cm3)
求高问题
5.一个圆柱体底面积是5平方分米,把它削成一个最大的圆锥,削去部分的体积是6立方分米,求这个圆柱的高是多少?
6÷(1- )=9(立方分米)
1
3
9÷5=1.8(分米)
木材加工问题
将圆木加工成最大的方木
2.将一根圆木(如下图)加工成最大的方木。
(1)方木的体积是多少立方米?
16 cm=0.16 m
0.16×(0.16+0.16)÷2×2=0.0512(m2)
0.0512×5=0.256(m3)
(2)废木料大约有多少立方米?(得数保留两位小数)
?
?
(3)几根方木的体积约是1立方米?
0.162×3.14×5-0.256≈0.15(m3)
1÷0.256≈4(根)
谢谢观赏
谢谢观赏
谢谢观赏
