四年级下册数学课件-三角形内角和-人教版(共26张PPT)
文档属性
| 名称 | 四年级下册数学课件-三角形内角和-人教版(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 14:14:55 | ||
图片预览





文档简介
(共26张PPT)
袁冲小学
猜谜语:
形状似座山,稳定性能坚
三竿首尾连,学问不简单
(打一几何图形)
学习目标
⑴探索并发现三角形的内角和是180°,能利用这个知识解决实际问题。
⑵学生在经历观察、猜测、验证的过程中,提升自身动手动脑及推理、归纳总结的能力。
自学指导:
1自学课本第67页例6.你知道什么是三角形的内角吗?三角形的内角和又怎么表示?三角形的内角和大约是多少度?
2通过量一量,折一折,拼一拼等方法来探索三角形的内角和有什么特性?
3通过探索你得出了什么结论?
1、什么是三角形的内角?
1
2
3
∠1+∠2+∠3
2、什么是三角形的内角和?
∠1,
∠2,
∠3
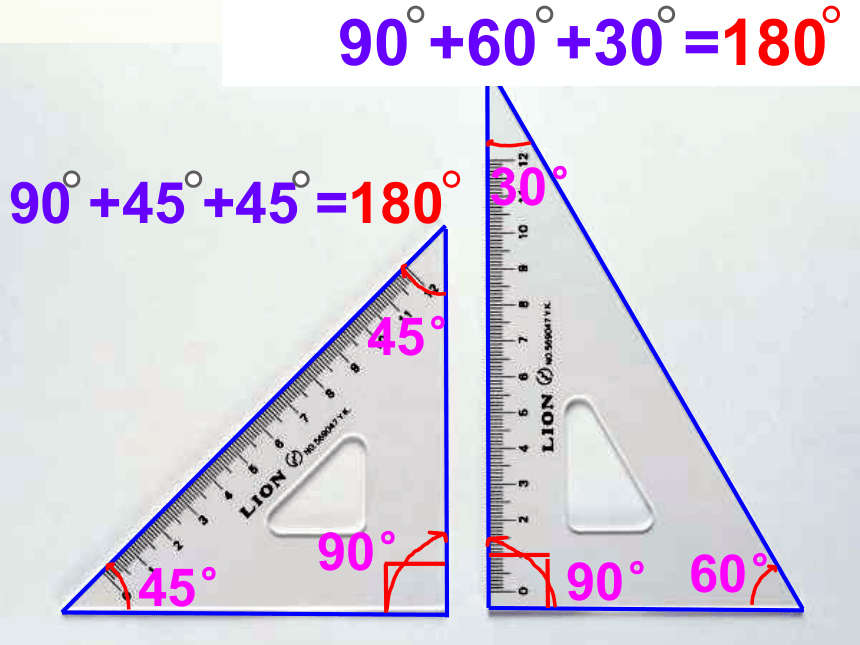
45°
45°
30°
60°
90°
90°
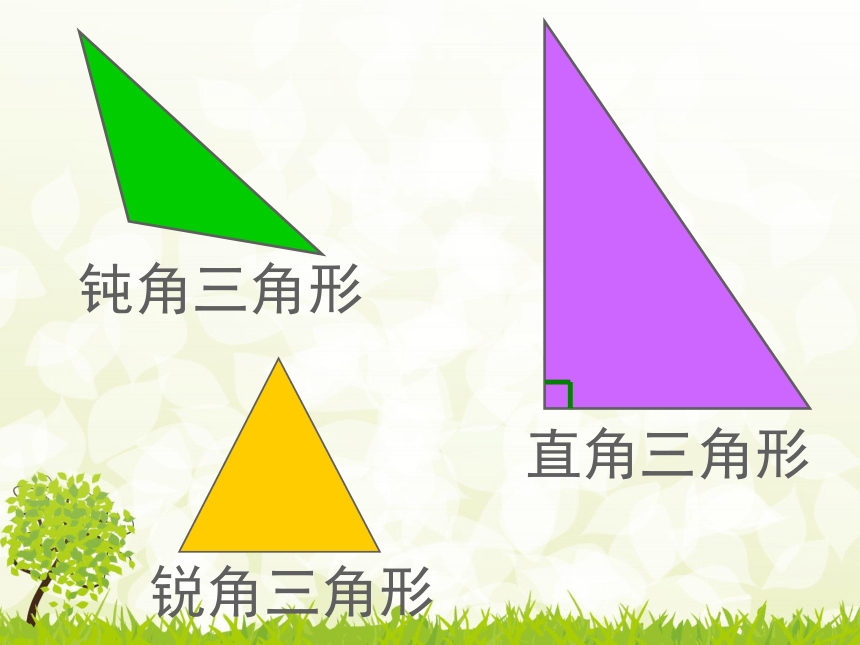
钝角三角形
直角三角形
锐角三角形
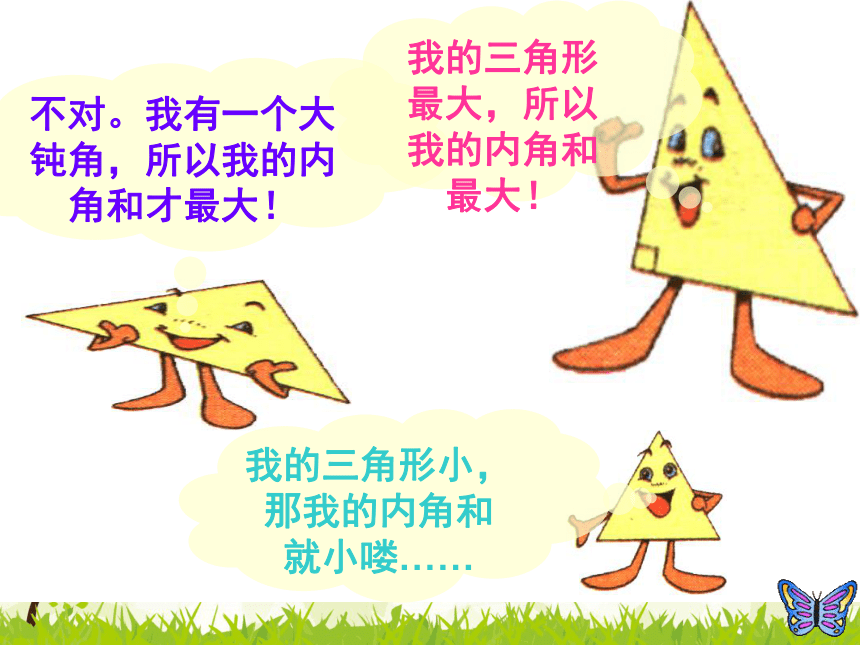
不对。我有一个大钝角,所以我的内角和才最大!
我的三角形小,那我的内角和就小喽……
我的三角形最大,所以我的内角和最大!
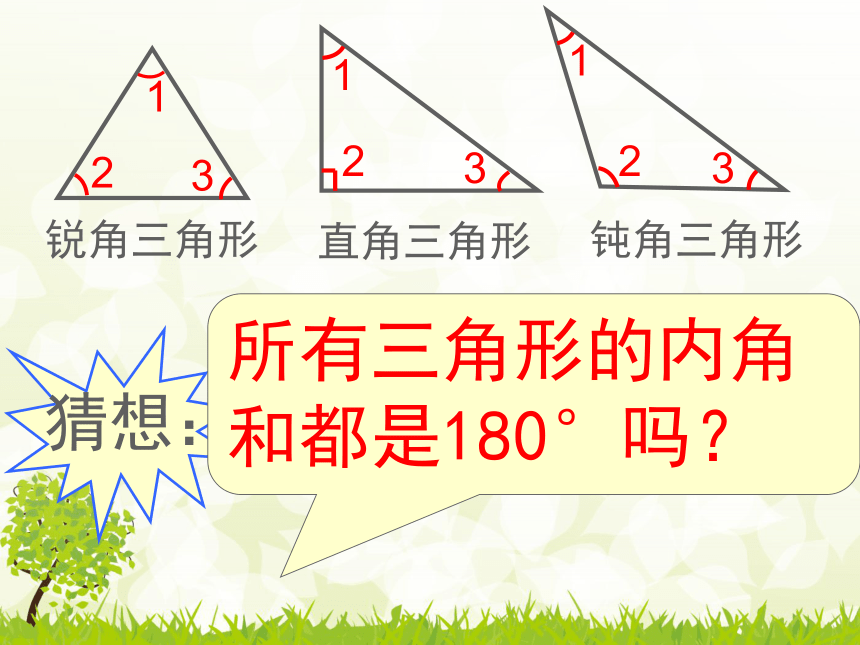
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
猜想:
所有三角形的内角和都是180°吗?
量一量:
1.八人一小组分工合作,动手
测量;
2.记录数据;
3.小组讨论:你发现了什么?
平角:180°
拼一拼:
折一折:
平角:180°
三角形的
内角和是180°
3.两个完全相同小直角三角形拼成一个大三角形,这个大三角形的内角和是多少度?
1.在一个三角形中能不能有两个直角?为什么?
有两个直角的图形不是三角形。
有两个钝角的图形不是三角形。
2.在一个三角形中能不能有两
个钝角?为什么?
一个三角形中最多只有一个直角或一个钝角
在一个三角形,∠1=140°,
∠3=25°,求∠2的度数.
①三角形越大,它的内角和就
越大。 ( )
②一个三角形的三个内角度数
是:70°,64°, 45°。(? )
(对的画“√”,错的画“×”)
×
×
请你来当数学小判官
③一个三角形至少有两个角是
锐角。 ( )
④钝角三角形的内角和大于锐
角三角形的内角和。 ( )
×
√
180°÷ 3 = 60°
求出三角形各个角的度数。
答:这个三角形三个内角的度数都是60°。
90°- 40°= 50°
答:这个三角形另外一个锐角的度数是50°。
(180°-96°)÷2 = 42°
答:这个三角形另外两个角的
度数都是42°。
这节课
你有什么收获?
1、书本第69页的第 1、2、3题。
2、选做:书本第70页的第7*题
袁冲小学
猜谜语:
形状似座山,稳定性能坚
三竿首尾连,学问不简单
(打一几何图形)
学习目标
⑴探索并发现三角形的内角和是180°,能利用这个知识解决实际问题。
⑵学生在经历观察、猜测、验证的过程中,提升自身动手动脑及推理、归纳总结的能力。
自学指导:
1自学课本第67页例6.你知道什么是三角形的内角吗?三角形的内角和又怎么表示?三角形的内角和大约是多少度?
2通过量一量,折一折,拼一拼等方法来探索三角形的内角和有什么特性?
3通过探索你得出了什么结论?
1、什么是三角形的内角?
1
2
3
∠1+∠2+∠3
2、什么是三角形的内角和?
∠1,
∠2,
∠3
45°
45°
30°
60°
90°
90°
钝角三角形
直角三角形
锐角三角形
不对。我有一个大钝角,所以我的内角和才最大!
我的三角形小,那我的内角和就小喽……
我的三角形最大,所以我的内角和最大!
锐角三角形
直角三角形
钝角三角形
1
2
3
1
1
2
2
3
3
猜想:
所有三角形的内角和都是180°吗?
量一量:
1.八人一小组分工合作,动手
测量;
2.记录数据;
3.小组讨论:你发现了什么?
平角:180°
拼一拼:
折一折:
平角:180°
三角形的
内角和是180°
3.两个完全相同小直角三角形拼成一个大三角形,这个大三角形的内角和是多少度?
1.在一个三角形中能不能有两个直角?为什么?
有两个直角的图形不是三角形。
有两个钝角的图形不是三角形。
2.在一个三角形中能不能有两
个钝角?为什么?
一个三角形中最多只有一个直角或一个钝角
在一个三角形,∠1=140°,
∠3=25°,求∠2的度数.
①三角形越大,它的内角和就
越大。 ( )
②一个三角形的三个内角度数
是:70°,64°, 45°。(? )
(对的画“√”,错的画“×”)
×
×
请你来当数学小判官
③一个三角形至少有两个角是
锐角。 ( )
④钝角三角形的内角和大于锐
角三角形的内角和。 ( )
×
√
180°÷ 3 = 60°
求出三角形各个角的度数。
答:这个三角形三个内角的度数都是60°。
90°- 40°= 50°
答:这个三角形另外一个锐角的度数是50°。
(180°-96°)÷2 = 42°
答:这个三角形另外两个角的
度数都是42°。
这节课
你有什么收获?
1、书本第69页的第 1、2、3题。
2、选做:书本第70页的第7*题
